Разбор первого тура Регионального этапа ВсОШ по ИИ 2025/2026¶
A. Натуральные числа¶
Условие:¶
В ряд выписали 100 натуральных чисел по очереди. Второе число было равно 1, а каждое число, начиная с третьего, равно сумме всех предыдущих выписанных чисел. Затем первое число стерли. Оказалось, что одно из оставшихся чисел равно 123456123456123456. Чему могло быть равно стертое число?
Решение:¶
Введём суммы $S_n=a_1+\dots+a_n$. Тогда при $n\ge3$
$$
S_n=S_{n-1}+a_n=S_{n-1}+\bigl(a_1+\dots+a_{n-1}\bigr)=2S_{n-1},
$$
откуда $S_n=2^{\,n-2}S_2=2^{\,n-2}(a_1+1)$. Следовательно, при $n\ge3$
$$
a_n=S_{n-1}=2^{\,n-3}(a_1+1).
$$
После стирания $a_1$ число $N=123456123456123456$ не может быть $a_2$, значит $N=a_n$ для некоторого $n\ge3$, то есть
$$
N=2^k(a_1+1)\quad(k\ge0),
$$
и потому
$$
a_1=\frac{N}{2^k}-1,
$$
причем любое $k$, при котором $a_1$ натуральное, подходит.
Ответ: 1929001929001928; 3858003858003857; 7716007716007715; 15432015432015431; 30864030864030863; 61728061728061727; 123456123456123455.
N = 123456123456123456
ans = []
k = 0
while N % (1 << k) == 0:
ans.append(N // (1 << k) - 1)
k += 1
for x in sorted(ans):
print(x)
1929001929001928 3858003858003857 7716007716007715 15432015432015431 30864030864030863 61728061728061727 123456123456123455
B. Матрицы и забытые активации¶
Условие:¶
Вася учится рисовать картинки с помощью нейросети: каждой точке на плоскости он хочет сопоставить цвет пикселя в трёх каналах (R, G, B).
На вход сеть получает вектор $$ x = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}, $$ а дальше несколько раз подряд делает одну и ту же операцию: умножает текущий вектор-столбец на матрицу весов и получает новый вектор-столбец. Размеры векторов, которые последовательно получаются внутри сети, таковы: $$ 2 \to 256 \to 128 \to 64 \to 3, $$ где $2$ — размер входного вектора, а $3$ — размер выходного вектора.
По невнимательности Вася забыл добавить в сеть всё «интересное» — и прибавление констант, и нелинейные функции. Поэтому вся работа сети до последнего шага — это только последовательные умножения на матрицы. Обозначим через $$ T(x_1,x_2) $$ трёхмерный вектор, который получается на самом последнем слое до финальной обработки.
Настоящий цвет пикселя Вася получает после по-координатного обрезания результата в диапазон от $0$ до $255$: $$ \operatorname{clip}(y)_i = \begin{cases} 0, & y_i < 0,\\ y_i, & 0 \le y_i \le 255,\\ 255, & y_i > 255, \end{cases} $$ и, наконец, $$ f(x_1,x_2) = \operatorname{clip}(T(x_1,x_2)). $$
В эксперименте с уже настроенными весами сети оказалось, что $$ f(-2,3) = \begin{pmatrix} 60 \\ 40 \\ 100 \end{pmatrix}, \qquad f(1,3) = \begin{pmatrix} 200 \\ 50 \\ 80 \end{pmatrix}. $$
Найдите вектор $f(-7,6).$
Решение:¶
Так как в сети нет ни прибавления констант, ни нелинейных функций, каждый слой делает преобразование вида
$$x \mapsto Wx,$$
для некоторой матрицы $W$.
Если применить два слоя подряд, получаем
$$x \mapsto W_2(W_1x)=(W_2W_1)x.$$
Поэтому вся сеть до обрезания эквивалентна одному умножению на некоторую матрицу $A$:
$$T(x_1,x_2)=A\begin{pmatrix}x_1\\x_2\end{pmatrix}.$$
Следовательно, $T$ — линейная функция, и для любых векторов $u,v$ и чисел $\alpha,\beta$ $$T(\alpha u+\beta v)=\alpha T(u)+\beta T(v).$$
В данных нам точках обрезание не меняет результат, поэтому $$ T(-2,3)=\begin{pmatrix}60\\40\\100\end{pmatrix}, \qquad T(1,3)=\begin{pmatrix}200\\50\\80\end{pmatrix}. $$
Представим искомый вектор через данные: $$(-7,6)=a(-2,3)+b(1,3).$$ Из равенства координат получаем систему $$ \begin{cases} -2a+b=-7,\\ 3a+3b=6. \end{cases} $$ Из второго уравнения $a+b=2$, откуда $a=3$, $b=-1$. Значит $$(-7,6)=3(-2,3)-(1,3).$$
По линейности $$ T(-7,6)=3T(-2,3)-T(1,3) =3\begin{pmatrix}60\\40\\100\end{pmatrix} -\begin{pmatrix}200\\50\\80\end{pmatrix} =\begin{pmatrix}-20\\70\\220\end{pmatrix}. $$
После обрезания $$ f(-7,6)=\operatorname{clip}\!\left(\begin{pmatrix}-20\\70\\220\end{pmatrix}\right) =\begin{pmatrix}0\\70\\220\end{pmatrix}. $$
Ответ: 0 70 220
C. Среднее и медиана¶
Условие:¶
Пусть $x_1,\dots,x_{10}\in[0,1]$ и выполнены условия $$ |x_i-x_j|\ge 0.01 \quad \text{для любых } i\ne j, $$ и любой подотрезок $[a,a+0.25]\subset[0,1]$ содержит хотя бы одну точку из множества $\{x_1,\dots,x_{10}\}$.
Отсортируем числа: $$ x_{(1)}\le x_{(2)}\le \dots \le x_{(10)}. $$ Обозначим $$ \overline x=\frac1{10}\sum_{k=1}^{10}x_{(k)},\qquad m=\frac{x_{(5)}+x_{(6)}}{2} $$ среднее и медиану (как среднее двух средних по порядку чисел).
Насколько максимально может отличаться среднее $\overline x$ от медианы $m$, то есть найдите $$ \max |\overline x - m| $$ при описанных условиях.
Первое решение:¶
Оценка.
Обозначим через $S=\sum_{k=1}^{10}x_{(k)}$, $a=x_{(5)}$, $b=x_{(6)}$, тогда $m=\dfrac{a+b}{2}$.
Из $|x_i-x_j|\ge 0.01$ следует, что соседние точки отличаются хотя бы на $0.01$. Значит $b=x_{(6)}\ge 0.05$.
Сумму первых пяти точек при фиксированном $a$ можно оценить, как: $$x_{(1)}+x_{(2)}+x_{(3)}+x_{(4)}+x_{(5)}\le (a-0.04)+(a-0.03)+(a-0.02)+(a-0.01)+a=5a-0.10.$$
Условие про каждый отрезок длины $0.25$ равносильно: между соседними точками нельзя оставить промежуток больше $0.25$. Сумма последних пяти точек при фиксированном $b$ в таком случае можно оценить сверху: $$x_{(6)}+x_{(7)}+x_{(8)}+x_{(9)}+x_{(10)}\le b+(b+0.25)+(b+0.50)+(b+0.75)+1=4b+2.50.$$
Складываем: $$S\le 5a+4b+2.40.$$
Теперь $$10(\overline x-m)=S-5(a+b)\le (5a+4b+2.40)-5a-5b=2.40-b.$$ Значит $$\overline x-m\le 0.24-0.1b\le 0.24-0.1\cdot 0.05=0.235.$$
Замена $x_i\mapsto 1-x_i$ сохраняет условия и меняет знак $\overline x-m$, поэтому $$\max|\overline x-m|\le 0.235.$$
Пример. $$0,\ 0.01,\ 0.02,\ 0.03,\ 0.04,\ 0.05,\ 0.30,\ 0.55,\ 0.80,\ 1.$$ Здесь достигается равенство, значит $$\max|\overline x-m|=0.235.$$
Ответ: 0.235
Второе решение (численно на Python):¶
Отсортируем точки $x_1 \le \dots \le x_{10}$. Тогда все условия задачи выражаются через соседние разности.
Минимальное расстояние между точками: $$ x_{i+1}-x_i \ge 0.01. $$
Условие, что любой подотрезок длины $0.25$ содержит точку, эквивалентно $$ x_{i+1}-x_i \le 0.25,\qquad x_1 \le 0.25,\qquad x_{10} \ge 0.75. $$
Среднее и медиана равны $$ \overline x=\frac1{10}\sum_{i=1}^{10}x_i,\qquad m=\frac{x_5+x_6}{2}. $$
Задача сводится к максимизации $|\overline x-m|$ при линейных ограничениях.
Численно она решается методом SLSQP (scipy.optimize.minimize), запуская
оптимизацию из нескольких начальных точек и выбирая лучший результат.
Для учёта модуля решаются две задачи: максимизация
$\overline x-m$ и максимизация $m-\overline x$.
Численный расчёт даёт $$ \max|\overline x-m| = 0.235, $$ что достигается, например, на конфигурации $$ (0,\;0.01,\;0.02,\;0.03,\;0.04,\;0.05,\;0.30,\;0.55,\;0.80,\;1.00). $$
import numpy as np
from scipy.optimize import minimize
N = 10
MIN_GAP = 0.01
MAX_GAP = 0.25
MID_L, MID_R = N//2 - 1, N//2
def mean_minus_median(x):
return x.mean() - 0.5*(x[MID_L] + x[MID_R])
CONS = (
[{"type": "ineq", "fun": (lambda x, i=i: (x[i+1]-x[i]) - MIN_GAP)} for i in range(N-1)] +
[{"type": "ineq", "fun": (lambda x, i=i: MAX_GAP - (x[i+1]-x[i]))} for i in range(N-1)] +
[{"type": "ineq", "fun": lambda x: MAX_GAP - x[0]},
{"type": "ineq", "fun": lambda x: x[-1] - (1 - MAX_GAP)}]
)
def best(sign, rng, R=300):
obj = lambda x: -sign * mean_minus_median(x)
best_val, best_x = -1e100, None
for _ in range(R):
x0 = np.sort(np.clip(np.linspace(0, 1, N) + rng.normal(0, 0.03, N), 0, 1))
res = minimize(obj, x0, method="SLSQP",
bounds=[(0, 1)]*N, constraints=CONS)
if res.success:
x = res.x
val = abs(mean_minus_median(x))
if val > best_val:
best_val, best_x = val, x.copy()
return best_val, best_x
rng = np.random.default_rng(1)
v1, x1 = best(+1, rng)
v2, x2 = best(-1, rng)
v, x = (v1, x1) if v1 >= v2 else (v2, x2)
print(f"max |mean-median| = {v:.6}",)
print(f"x = {np.round(x, 6)}", )
print(f"mean, median, diff = {x.mean():.6} {0.5*(x[MID_L]+x[MID_R]):.6} {mean_minus_median(x):.6}")
max |mean-median| = 0.235 x = [0. 0.01 0.02 0.03 0.04 0.05 0.3 0.55 0.8 1. ] mean, median, diff = 0.28 0.045 0.235
D. MAE¶
Условие:¶
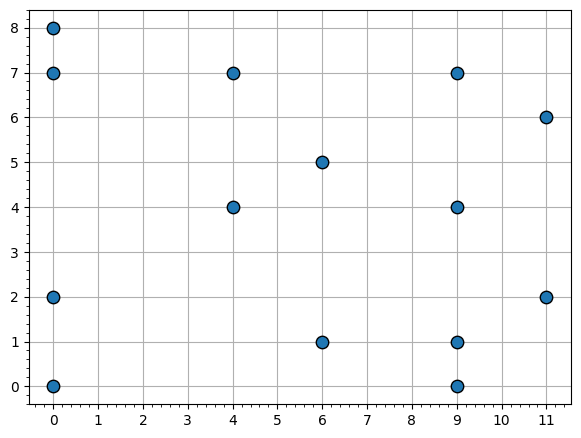
Есть выборка из $N=14$ наблюдений (на рисунке). Каждая точка задаётся парой координат ($x_i, y_i$).
Рассмотрим линейное предсказание $\hat{y}(x)=a\cdot x+b$. Найдите минимальное $$MAE = \frac{1}{N}\sum_{i=1}^{N} |\hat{y}(x_i)-y_i|$$ этого предсказания на выборке ($x_i, y_i$) по всем $a, b$.
Первое решение:¶
Сгруппируем точки по одинаковым $x$ (по «вертикалям»). Для фиксированного $x=c$ все слагаемые имеют вид $$\sum |(ac+b)-y|=\sum |\hat y(c)-y|.$$ Если менять только $\hat y(c)$, то минимум достигается, когда $\hat y(c)$ делит множество данных нам $y$ на две равные части: если увеличить $\hat y(c)$ на маленькое $t$, то расстояния до точек ниже $\hat y(c)$ увеличатся на $t$ каждое, а до точек выше $\hat y(c)$ уменьшатся на $t$ каждое. Тогда если с одной из сторон от $\hat y(c)$ точек меньше, то мы можем ее подвинуть и уменьшить mae. Значит минимум получается, когда $\hat y(c)$ между двумя серединными $y$.
Найдём для каждого столбца такой промежуток и минимальную сумму.
- $x=0$: $y=0,2,7,8$, значит $t\in[2,7]$, минимум суммы равен $13$.
- $x=4$: $y=4,7$, значит $t\in[4,7]$, минимум суммы равен $3$.
- $x=6$: $y=1,5$, значит $t\in[1,5]$, минимум суммы равен $4$.
- $x=9$: $y=0,1,4,7$, значит $t\in[1,4]$, минимум суммы равен $10$.
- $x=11$: $y=2,6$, значит $t\in[2,6]$, минимум суммы равен $4$.
Если найдётся прямая $\hat y(x)=ax+b$, которая на каждом из этих $x$ попадает в соответствующий промежуток, то общая сумма модулей будет равна сумме минимумов по столбцам.
Прямая $\hat y(x)=4$ подходит, и потому $$MAE_{\min}=\frac{34}{14}=\frac{17}{7}.$$
Ответ: 2.4285714286
Второе решение:¶
import numpy as np
import pandas as pd
from scipy.optimize import minimize
df = pd.read_csv("points.csv")
x = df["x"].to_numpy(float)
y = df["y"].to_numpy(float)
def mae(p):
a, b = p
return np.mean(np.abs(a*x + b - y))
res = minimize(mae, x0=[0.0, 0.0])
a, b = res.x
print("a =", a)
print("b =", b)
print("min MAE =", mae([a, b]))
print("success =", res.success)
a = -0.2582266971454471 b = 5.41700795527777 min MAE = 2.4285714285714284 success = True
Третье решение:¶
import numpy as np
import pandas as pd
import random, math
df = pd.read_csv("points.csv")
n = len(df)
xs = df["x"].to_numpy(float)
ys = df["y"].to_numpy(float)
minx, maxx = min(xs), max(xs)
miny, maxy = min(ys), max(ys)
span = max(maxx - minx, maxy - miny) or 1.0
ax0, ax1 = minx - 2*span, maxx + 2*span
ay0, ay1 = miny - 2*span, maxy + 2*span
random.seed(42)
bestL, besta, bestb = 1e30, 0.0, 0.0
M = 100_000
for _ in range(M):
x0 = random.uniform(ax0, ax1)
y0 = random.uniform(ay0, ay1)
th = random.uniform(-math.pi/2 + 1e-6, math.pi/2 - 1e-6)
a = math.tan(th)
b = y0 - a * x0
s = 0.0
for xi, yi in zip(xs, ys):
s += abs(a * xi + b - yi)
L = s / n
if L < bestL:
bestL, besta, bestb = L, a, b
print(f"a = {besta}\nb = {bestb}\nmin MAE = {bestL}")
a = -0.007780643998228674 b = 4.04808442288716 min MAE = 2.4285714285714284
Четвёртое решение:¶
Линейно меняя а,b MAE меняется линейно, пока один из модулей не поменяет знак. Нетрудно видеть, что линейно меняя а,b, так чтобы прямая не перепрыгивала через точки можно подвинуть прямую так, чтобы она проходила через 2 точки выборки. Давайте теперь кодом среди всех прямых, проходящих через 2 точки выборки выберем оптимальную прямую - с наименьшим MAE.
import numpy as np
import pandas as pd
import random, math
df = pd.read_csv("points.csv")
n = len(df)
xs = df["x"].to_numpy(float)
ys = df["y"].to_numpy(float)
bestL, besta, bestb = 1e30, 0.0, 0.0
for i in range(n):
xi, yi = xs[i], ys[i]
for j in range(i+1, n):
dx = xs[j] - xi
if dx == 0.0:
continue
a = (ys[j] - yi) / dx
b = yi - a * xi
s = 0.0
for k in range(n):
s += abs(a * xs[k] + b - ys[k])
L = s / n
if L < bestL:
bestL, besta, bestb = L, a, b
print(besta, bestb, bestL)
-0.3333333333333333 7.0 2.4285714285714284
E. Прямая крутится¶
Условие:¶
Представим, что у нас есть прямоугольник, раскрашенный в два цвета: часть его площади белая, часть — чёрная. Нам нужно классифицировать точки внутри прямоугольника по цвету.
Мы используем очень простой классификатор: проводим через центр прямоугольника прямую $L$. Всё, что лежит по одну сторону от этой прямой, считаем чёрным, а всё, что по другую сторону, считаем белым.
Теперь посмотрим, как хорошо такая прямая может “угадать” разметку. Для любой выбранной прямой $L$ можно вычислить долю площади, где предсказанный цвет совпадает с настоящим.
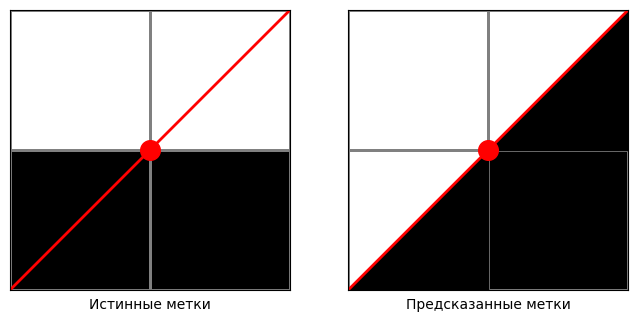
Рассмотрим пример квадрата $2\times 2$. Легко видеть, что доля правильно предсказанной площади равна 0.75.
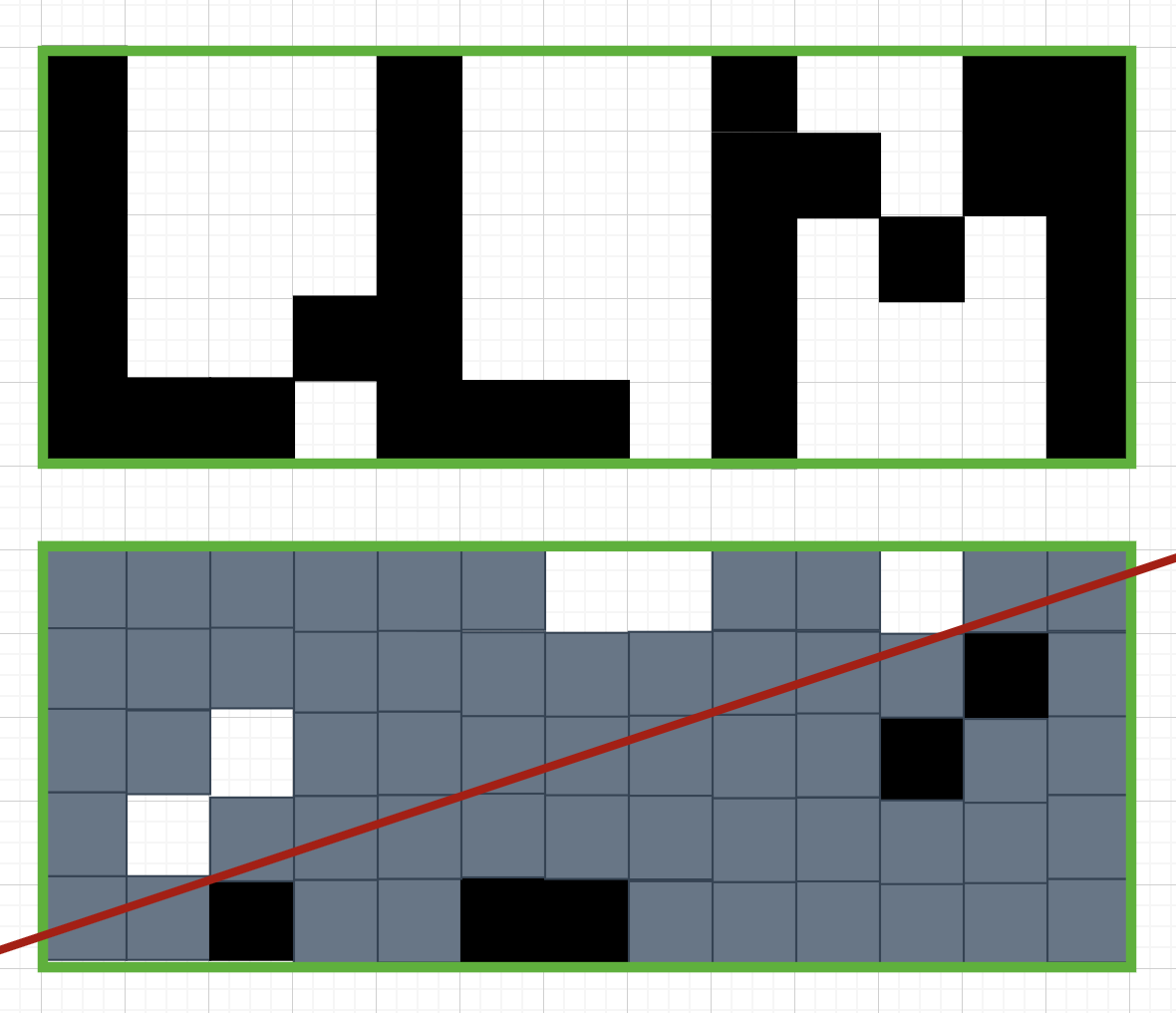
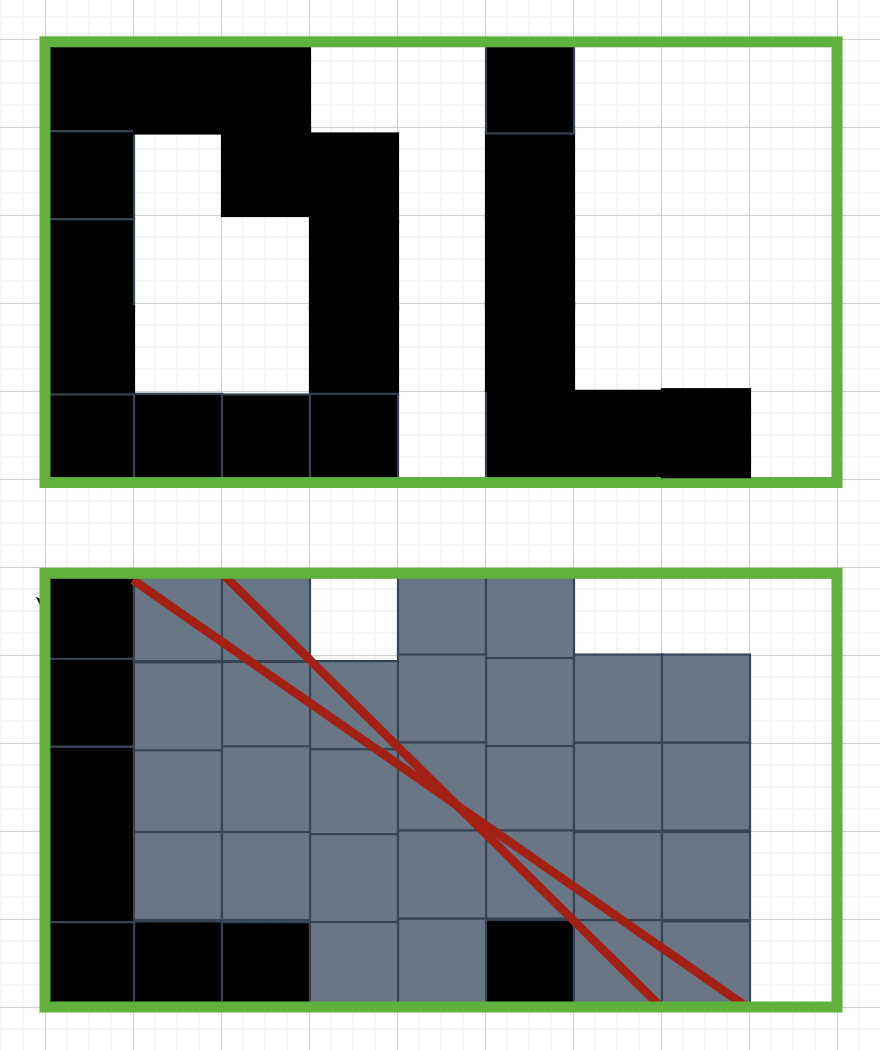
Среди всех прямых L, проходящих через центр прямоугольника, какое наибольшее значение может принимать доля площади, предсказанной правильно? Посчитайте ответы для каждой из трех картинок ниже.
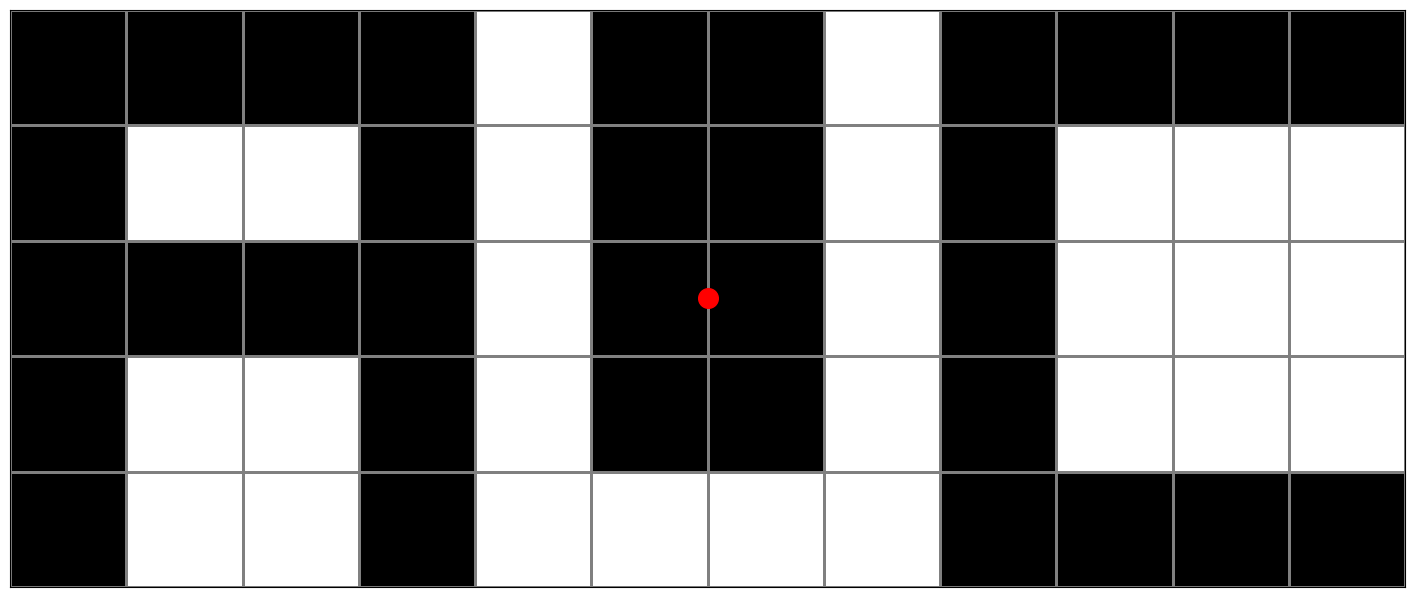
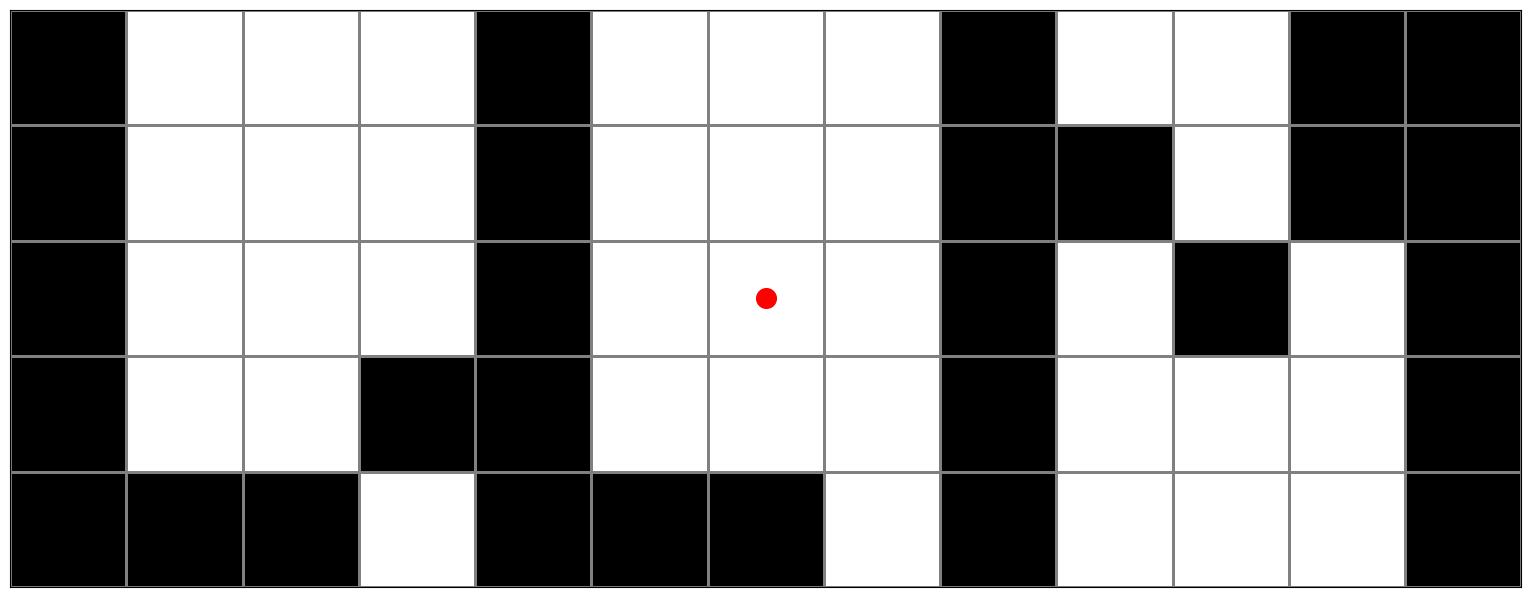
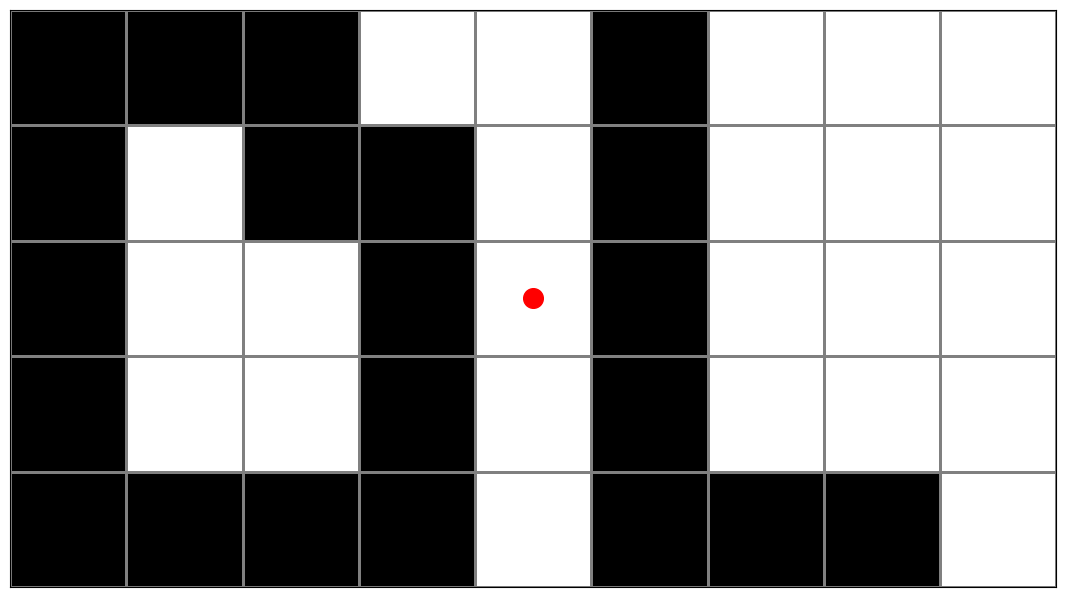
Первое решение:¶
Рассмотрим центрально симметричные клетки. Если они одного цвета, то любая прямая $L$ будет правильно классифицировать ровно половину площади внутри них. Для оставшихся разноцветных пар в каждой подзадаче существует разделяющая их прямая, она и делает лучшую классификацию.
Ответ: 0.6500000 0.5769230769 0.7000000

Второе решение:¶
import sys, math, random
from tqdm import tqdm
def best_line(grid, N=20000, P=200000, seed=1):
random.seed(seed)
n, m = len(grid), len(grid[0])
cx, cy = m/2.0, n/2.0
dx = [0.0]*P
dy = [0.0]*P
lab = [0]*P
for i in range(P):
x = random.random()*m
y = random.random()*n
ix, iy = int(x), int(y)
lab[i] = grid[iy][ix]
dx[i] = x - cx
dy[i] = y - cy
best = -1.0
best_t = 0.0
best_flip = 1
for k in tqdm(range(N)):
t = 2.0*math.pi*k/N
nx, ny = -math.sin(t), math.cos(t)
c1 = 0
c2 = 0
for i in range(P):
side = (dx[i]*nx + dy[i]*ny) >= 0.0
if (1 if side else 0) == lab[i]: c1 += 1
if (0 if side else 1) == lab[i]: c2 += 1
acc1 = c1 / P
acc2 = c2 / P
if acc2 > acc1:
acc1, best_flip_cur = acc2, 0
else:
best_flip_cur = 1
if acc1 > best:
best = acc1
best_t = t
best_flip = best_flip_cur
return best, best_t, best_flip
if __name__ == "__main__":
grid = [
[1,1,1,1,0,1,1,0,1,1,1,1],
[1,0,0,1,0,1,1,0,1,0,0,0],
[1,1,1,1,0,1,1,0,1,0,0,0],
[1,0,0,1,0,1,1,0,1,0,0,0],
[1,0,0,1,0,0,0,0,1,1,1,1],
]
acc, theta, flip = best_line(grid, N=20_000, P=40_000, seed=1)
print(f"{acc:.6f} {theta:.6f} {'pos_black' if flip else 'neg_black'}")
100%|██████████| 20000/20000 [02:49<00:00, 117.89it/s]
0.652050 2.847540 pos_black
F. NLP¶
Условие:¶
Петя изучает язык, в котором алфавит состоит из букв: $$ \{A,D,E,I,L,M,N,S,T\}. $$
Изначально написано слово $DS$.
Затем на каждом шаге к слову справа приписывается ещё одна буква.
Выбор новой буквы зависит исключительно от последней буквы текущего слова.
Правила для приписывания новой буквы такие:
- Если последняя буква - $A$ равновероятно добавляется одна из $\{M, D\}$.
- Если последняя буква $E$ или $I$ равновероятно добавляется одна из $\{T, S, M\}$.
- Если последняя буква $T$ или $M$ равновероятно добавляется одна из $\{L, N\}$.
- Если последняя буква $N$ или $D$ равновероятно добавляется одна из $\{A, I\}$.
- Если последняя буква $S$ или $L$ равновероятно добавляется одна из $\{E, I, D\}$.
Петя очень азартный человек. Он ждёт, когда в строке появится подстрока $ML$. Найдите математическое ожидание числа шагов (то есть приписанных букв), необходимых для того, чтобы это случилось.
Первое решение:¶
Обозначим через $E_X$ математическое ожидание числа приписанных букв до первого появления подстроки $ML$, если последняя буква текущего слова равна $X$. Стартовое слово $DS$, значит требуется $E_S$.
Для любой последней буквы $X$ верно $$ E_X=1+\sum_Y p_{X\to Y}\,E_Y, $$ кроме случая $X=M$: при переходе $M\to L$ подстрока $ML$ появляется сразу, поэтому $$ E_M=\tfrac12\cdot 1+\tfrac12(1+E_N)=1+\tfrac12E_N. $$
По правилам получаем систему на $E_A,E_D,E_E,E_I,E_L,E_M,E_N,E_S,E_T$: $$ \begin{aligned} E_A&=1+\frac{E_M+E_D}{2},\\ E_E&=1+\frac{E_T+E_S+E_M}{3},\\ E_I&=1+\frac{E_T+E_S+E_M}{3},\\ E_T&=1+\frac{E_L+E_N}{2},\\ E_M&=1+\frac{E_N}{2},\\ E_N&=1+\frac{E_A+E_I}{2},\\ E_D&=1+\frac{E_A+E_I}{2},\\ E_S&=1+\frac{E_E+E_I+E_D}{3},\\ E_L&=1+\frac{E_E+E_I+E_D}{3}. \end{aligned} $$
Переносим всё в левую часть, получаем матричное уравнение $A\mathbf{E}=\mathbf{b}$, решаем и берём компоненту $E_S$. Ответ: $$ E_S=\frac{173}{12} = 14.41(6). $$
Ответ: 14.41666666666666666666
import numpy as np
# порядок неизвестных: [A, D, E, I, L, M, N, S, T]
A = np.array([
[ 1, -1/2, 0, 0, 0, -1/2, 0, 0, 0], # EA = 1 + (EM+ED)/2
[ 0, 0, 1, 0, 0, -1/3, 0, -1/3, -1/3], # EE = 1 + (ET+ES+EM)/3
[ 0, 0, 0, 1, 0, -1/3, 0, -1/3, -1/3], # EI = 1 + (ET+ES+EM)/3
[ 0, 0, 0, 0, -1/2, 0, -1/2, 0, 1], # ET = 1 + (EL+EN)/2
[ 0, 0, 0, 0, 0, 1, -1/2, 0, 0], # EM = 1 + EN/2
[-1/2,0, 0, -1/2, 0, 0, 1, 0, 0], # EN = 1 + (EA+EI)/2
[-1/2,1, 0, -1/2, 0, 0, 0, 0, 0], # ED = 1 + (EA+EI)/2
[ 0,-1/3, -1/3,-1/3, 0, 0, 0, 1, 0], # ES = 1 + (EE+EI+ED)/3
[ 0,-1/3, -1/3,-1/3, 1, 0, 0, 0, 0], # EL = 1 + (EE+EI+ED)/3
], dtype=float)
b = np.ones(9)
E = np.linalg.inv(A) @ b
labels = ["A","D","E","I","L","M","N","S","T"]
print("E_S ≈", E[labels.index("S")])
E_S ≈ 14.416666666666664
Второе решение:¶
Решим задачу с помощью метода Монте-Карло. То есть промоделируем процесс, описанный в условии. Тогда, по закону больших чисел (ЗБЧ), при достаточно большом числе попыток среднее значение по нашим запускам будет находиться достаточно близко к истинному ответу.
import random
next_letters = {
"A": ["M", "D"],
"E": ["T", "S", "M"],
"I": ["T", "S", "M"],
"T": ["L", "N"],
"M": ["L", "N"],
"N": ["A", "I"],
"D": ["A", "I"],
"S": ["E", "I", "D"],
"L": ["E", "I", "D"],
}
def one_run():
last = "S" # стартовое слово "DS"
steps = 0
while True:
nxt = random.choice(next_letters[last])
steps += 1
if last == "M" and nxt == "L": # появилась подстрока "ML"
return steps
last = nxt
TRIALS = 10_000_000
avg = sum(one_run() for _ in range(TRIALS)) / TRIALS
print(avg)
14.4200713
G. Отрезки¶
Условие:¶
На общем сервере запланированы запуски обучения модели одинаковой длительности. Каждый запуск — отрезок времени. Концы всех отрезков различны. Администратор настроил очередь так, что в любой момент времени сервер занят максимум двумя такими запусками.
Пусть $A$ — число способов выбрать непустой набор запусков, которые можно провести без пересечений по времени.
Для примера:
- если на прямой расположен один отрезок, то $A = 1$;
- если расположены два пересекающихся отрезка, то $A = 2$;
- если расположены два непересекающихся отрезка, то $A = 3$.
Какие значение из отрезка $[1500; 2025]$ может принимать величина $A$?
Решение:¶
Будем решать задачу в терминах отрезков на прямой. Пусть имеется $n$ отрезков, причём $i$-й и $(i+1)$-й отрезки пересекаются, а отрезки с индексами, отличающимися хотя бы на $2$, не пересекаются. Обозначим через $f(n)$ количество способов выбрать из них подмножество непересекающихся отрезков (пустое множество разрешено). Тогда легко видеть, что $f(1) = 1 = f(2)$. Кроме того, $f(n) = f(n-1)+f(n-2)$ при всех $n \geqslant 3$. Дейстивительно, рассмотрим $n$-й отрезок. Если он выбран, то $n-1$-й не выбран, и все сводится к выбору подмножества из первых $n-2$ отрезков, число таких способов $f(n-2)$. В противном случае, мы выбираем отрезки лишь из первых $n-1$, число таких способов $f(n-1)$. Из сказанного выше следует, что множество значений $f$ — числа Фибоначчи. Произвольное разрешенное условием расположение отрезков представляет собой объединение нескольких групп, изучаемых выше, поэтому количество способов выбрать подмножество непересекающихся отрезков принимает значения, которые представляются в виде произведения нескольких чисел Фиббоначчи, эта величина по условию равна $A+1$, поскольку пустое множество в $A$ не учтено. Компьютерный перебор* показывает, что числа такого вида из отрезка [1500; 2025] — это
Ответ: 1507 1511 1520 1529 1535 1559 1574 1596 1599 1601 1619 1624 1631 1637 1649 1663 1679 1689 1699 1700 1727 1754 1759 1763 1767 1779 1799 1829 1835 1863 1868 1869 1871 1874 1884 1889 1919 1943 1949 1973 1979 1999 2015 2024
Компьютерный перебор:
LOW, HIGH = 1500, 2025
MAXP = HIGH + 1
# Фибоначчи до MAXP
fib = [1, 1]
while fib[-1] + fib[-2] <= MAXP:
fib.append(fib[-1] + fib[-2])
fibs = sorted(set(v for v in fib if v >= 2))
reachable = {1}
changed = True
while changed:
changed = False
new_vals = set()
for p in reachable:
for f in fibs:
q = p * f
if q <= MAXP and q not in reachable:
new_vals.add(q)
if new_vals:
reachable |= new_vals
changed = True
ans = sorted(p - 1 for p in reachable if LOW + 1 <= p <= HIGH + 1)
print(*ans)
1507 1511 1520 1529 1535 1559 1574 1596 1599 1601 1619 1624 1631 1637 1649 1663 1679 1689 1699 1700 1727 1754 1759 1763 1767 1779 1799 1829 1835 1863 1868 1869 1871 1874 1884 1889 1919 1943 1949 1973 1979 1999 2015 2024
H. Одинокий круг¶
Условие:¶
Андрей готовится к собеседованию на стажировку по машинному обучению.
Чтобы разобраться с базовыми идеями классификации, он начал с самого простого случая:
если точки двух классов на плоскости можно разделить прямой, то метод опорных векторов (SVM)
строит разделяющую прямую
$$
w_1 x + w_2 y + b = 0,
$$
и знак выражения $w_1 x + w_2 y + b$ определяет, к какому классу относится точка (с одной стороны от прямой все точки будут иметь знак $+$, а с другой $-$).
Так Андрей познакомился с линейной классификацией.
Он нашёл простой пример кода, который показывает, как можно считать точки из стандартного ввода,
записать их в таблицу с колонками x, y, label и обучить по этим данным линейный SVM:
import sys
import pandas as pd
from sklearn.svm import SVC
def read_points():
data = []
tokens = sys.stdin.read().split()
it = iter(tokens)
n = int(next(it))
for _ in range(n):
x = float(next(it))
y = float(next(it))
label = int(next(it))
data.append((x, y, label))
df = pd.DataFrame(data, columns=["x", "y", "label"])
return df
df = read_points()
clf = SVC(kernel="linear")
clf.fit(df[["x", "y"]], df["label"])
w1, w2 = clf.coef_[0]
b = clf.intercept_[0]
print(w1, w2, b)
Однако на собеседовании Андрею досталась другая задача.
Даны точки на плоскости с метками классов $-1$ и $+1$.
Гарантируется, что существует окружность с центром $(x_0,y_0)$ и радиусом $R>0$ такая, что
- все точки класса $-1$ лежат строго внутри этой окружности;
- все точки класса $+1$ лежат строго вне этой окружности.
Нужно найти любую такую окружность $(x_0, y_0, R)$.
Помогите Андрею решить эту задачу и пройти собеседование!
Первое решение:¶
Окружность задаётся уравнением $$ (x-x_0)^2+(y-y_0)^2=R^2. $$ Раскроем скобки: $$ x^2+y^2-2x_0x-2y_0y+(x_0^2+y_0^2-R^2)=0. $$ Это линейное выражение по признакам $$ \bigl(x^2+y^2,\ x,\ y\bigr). $$ Поэтому можно обучить линейный SVM в этом пространстве признаков и получить разделение вида $$ w_0(x^2+y^2)+w_1x+w_2y+b=0. $$ Из него восстанавливается окружность: $$ x_0=-\frac{w_1}{2w_0},\qquad y_0=-\frac{w_2}{2w_0},\qquad R^2=x_0^2+y_0^2-\frac{b}{w_0}. $$ Однако, у этих признаков обычно разные масштабы (особенно у $r^2$), поэтому перед обучением делаем стандартную нормировку каждого признака отдельно: $$X'=\frac{X-\mu}{\sigma},$$ где $\mu$ и $\sigma$ — векторы средних и стандартных отклонений по выборке (деление покомпонентное).
SVM в нормированных признаках даёт $$w'\cdot X' + b' = 0.$$ Подставляем $X'=(X-\mu)/\sigma$ и получаем уравнение в исходных признаках: $$w\cdot X + b = 0,$$ где $$w=\frac{w'}{\sigma},\qquad b=b'-w'\cdot\frac{\mu}{\sigma}.$$
После этого имеем $$w_0r^2+w_1x+w_2y+b=0,$$ и отсюда центр и радиус окружности: $$x_0=-\frac{w_1}{2w_0},\qquad y_0=-\frac{w_2}{2w_0},\qquad R=\sqrt{x_0^2+y_0^2-\frac{b}{w_0}}.$$
import sys
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
import numpy as np
import math
def read_points():
it = iter(sys.stdin.read().split())
n = int(next(it))
xs = np.empty(n, dtype=float)
ys = np.empty(n, dtype=float)
labels = np.empty(n, dtype=int)
for i in range(n):
xs[i] = float(next(it))
ys[i] = float(next(it))
labels[i] = int(next(it))
return xs, ys, labels
xs, ys, y = read_points()
X = np.column_stack([xs*xs + ys*ys, xs, ys])
scaler = StandardScaler()
Xs = scaler.fit_transform(X)
clf = SVC(kernel="linear", C=1e6)
clf.fit(Xs, y)
w_s = clf.coef_[0]
b_s = clf.intercept_[0]
mu = scaler.mean_
sd = scaler.scale_
w = w_s / sd
b = b_s - np.dot(w_s, mu / sd)
w0, w1, w2 = w
x0 = -w1 / (2 * w0)
y0 = -w2 / (2 * w0)
R2 = x0*x0 + y0*y0 - b / w0
R = math.sqrt(R2)
print(x0, y0, R)
Второе решение:¶
Решим задачу с помощью Монте-Карло. Будем генерировать точку центра, после этого будем проверять можно ли подобрать радиус, чтобы выполнилось условие.
import sys, math, random
it = iter(sys.stdin.read().split())
n = int(next(it))
pts = [(float(next(it)), float(next(it)), int(next(it))) for _ in range(n)]
xs, ys = [], []
for x, y, _ in pts:
xs.append(x)
ys.append(y)
minx, maxx, miny, maxy = min(xs), max(xs), min(ys), max(ys)
span = max(maxx-minx, maxy-miny) or 1.0
ax0, ax1, ay0, ay1 = minx-2*span, maxx+2*span, miny-2*span, maxy+2*span
random.seed(42)
def check(x0,y0):
d_in = 0.0
d_out = float("inf")
for x,y,l in pts:
d = (x-x0)*(x-x0) + (y-y0)*(y-y0)
if l == -1:
if d > d_in: d_in = d
else:
if d < d_out: d_out = d
if d_in < d_out:
print(f"{x0:.10f} {y0:.10f} {math.sqrt((d_in+d_out)/2):.10f}")
return True
return False
for _ in range(500_000):
if check(random.uniform(ax0,ax1), random.uniform(ay0,ay1)):
break