scipy.signal.windows.

bartlett

scipy.signal.windows.bartlett(M, sym=True, *, xp=None, device=None)

Возвращает окно Бартлетта.

Окно Бартлетта очень похоже на треугольное окно, за исключением того, что конечные точки находятся на нуле. Оно часто используется в обработке сигналов для сужения сигнала без создания слишком большого колебания в частотной области.

Параметры:

Mint

Первая строка матрицы. Если None,

symbool, необязательно

Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.

xparray_namespace, опционально

Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию: numpy

устройство: любое

необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в xp.

Возвращает:

wndarray

Треугольное окно, с первым и последним отсчётами, равными нулю, и максимальным значением, нормализованным до 1 (хотя значение 1 не появляется, если M четно и sym равно True).

Смотрите также

triang

Треугольное окно, которое не касается нуля на концах

Примечания

Окно Бартлетта определяется как

\[w(n) = \frac{2}{M-1} \left( \frac{M-1}{2} - \left|n - \frac{M-1}{2}\right| \right)\]

Большинство ссылок на окно Бартлетта происходят из литературы по обработке сигналов, где оно используется как одна из многих оконных функций для сглаживания значений. Обратите внимание, что свёртка с этим окном даёт линейную интерполяцию. Оно также известно как аподизация (что означает "удаление ноги", т.е. сглаживание разрывов в начале и конце дискретизированного сигнала) или сужающаяся функция. Преобразование Фурье окна Бартлетта является произведением двух функций sinc. Обратите внимание на отличное обсуждение в Kanasewich. [2]

Ссылки

[1]

M.S. Bartlett, «Periodogram Analysis and Continuous Spectra», Biometrika 37, 1-16, 1950.

[2]

E.R. Kanasewich, «Time Sequence Analysis in Geophysics», The University of Alberta Press, 1975, стр. 109-110.

[3]

A.V. Oppenheim и R.W. Schafer, «Discrete-Time Signal Processing», Prentice-Hall, 1999, стр. 468-471.

[4]

Википедия, "Оконная функция", https://en.wikipedia.org/wiki/Window_function

[5]

W.H. Press, B.P. Flannery, S.A. Teukolsky и W.T. Vetterling, «Numerical Recipes», Cambridge University Press, 1986, страница 429.

Примеры

Попробуйте в вашем браузере!

Построить окно и его частотную характеристику:

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

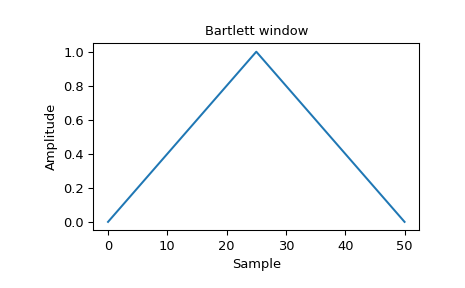
>>> window = signal.windows.bartlett(51)
>>> plt.plot(window)
>>> plt.title("Bartlett window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

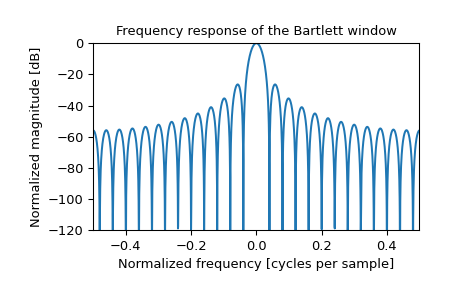
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Bartlett window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

НазадОткрыть во вкладке