blackman#
- scipy.signal.windows.blackman(M, sym=True, *, xp=None, device=None)[источник]#
Вернуть окно Блэкмана.
Окно Блэкмана - это сужение, образованное использованием первых трех членов суммы косинусов. Оно было разработано для минимально возможной утечки. Оно близко к оптимальному, лишь немного хуже окна Кайзера.
- Параметры:
- Mint
Первая строка матрицы. Если None,
- symbool, необязательно
Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.
- xparray_namespace, опционально
Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию:
numpy- устройство: любое
необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в
xp.
- Возвращает:
- wndarray
Окно, с максимальным значением, нормализованным до 1 (хотя значение 1 не появляется, если M четно и sym равно True).
Примечания
Окно Блэкмана определяется как
\[w(n) = 0.42 - 0.5 \cos(2\pi n/M) + 0.08 \cos(4\pi n/M)\]Окно «точного Блэкмана» было разработано для обнуления третьего и четвёртого боковых лепестков, но имеет разрывы на границах, что приводит к спаду 6 дБ/окт. Это окно является аппроксимацией «точного» окна, которое не так хорошо обнуляет боковые лепестки, но гладкое на краях, улучшая скорость спада до 18 дБ/окт. [3]
Большинство ссылок на окно Блэкмана происходят из литературы по обработке сигналов, где оно используется как одна из многих оконных функций для сглаживания значений. Оно также известно как аподизация (что означает “удаление ноги”, т.е. сглаживание разрывов в начале и конце дискретизированного сигнала) или сужающая функция. Оно известно как “почти оптимальная” сужающая функция, почти такая же хорошая (по некоторым мерам), как окно Кайзера.
Ссылки
[1]Блэкман, Р.Б. и Тьюки, Дж.В., (1958) Измерение спектров мощности, Dover Publications, Нью-Йорк.
[2]Оппенгейм, А.В., и Р.В. Шафер. Обработка дискретных сигналов. Верхняя Сэдл-Ривер, Нью-Джерси: Prentice-Hall, 1999, стр. 468-471.
[3]Харрис, Фредерик Дж. (январь 1978). "Об использовании окон для гармонического анализа с дискретным преобразованием Фурье". Proceedings of the IEEE 66 (1): 51-83. DOI:10.1109/PROC.1978.10837.
Примеры
Построить окно и его частотную характеристику:
>>> import numpy as np >>> from scipy import signal >>> from scipy.fft import fft, fftshift >>> import matplotlib.pyplot as plt
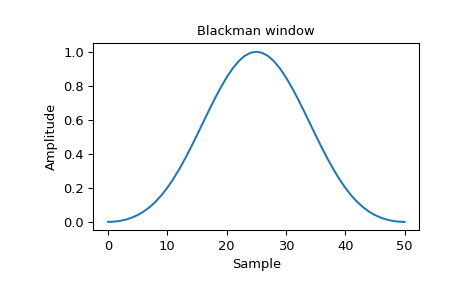
>>> window = signal.windows.blackman(51) >>> plt.plot(window) >>> plt.title("Blackman window") >>> plt.ylabel("Amplitude") >>> plt.xlabel("Sample")
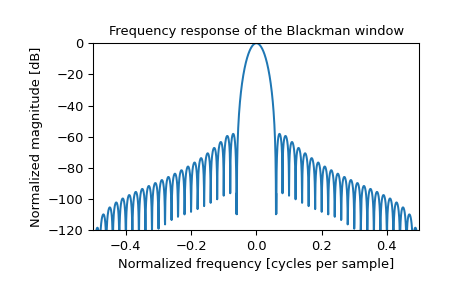
>>> plt.figure() >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = np.abs(fftshift(A / abs(A).max())) >>> response = 20 * np.log10(np.maximum(response, 1e-10)) >>> plt.plot(freq, response) >>> plt.axis([-0.5, 0.5, -120, 0]) >>> plt.title("Frequency response of the Blackman window") >>> plt.ylabel("Normalized magnitude [dB]") >>> plt.xlabel("Normalized frequency [cycles per sample]")