chebwin#
- scipy.signal.windows.chebwin(M, в, sym=True, *, xp=None, device=None)[источник]#
Возвращает окно Дольфа-Чебышева.
- Параметры:
- Mint
Первая строка матрицы. Если None,
- вfloat
Затухание (в дБ).
- symbool, необязательно
Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.
- xparray_namespace, опционально
Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию:
numpy- устройство: любое
необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в
xp.
- Возвращает:
- wndarray
Окно, с максимальным значением, всегда нормализованным до 1
Примечания
Это окно оптимизирует наименьшую ширину главного лепестка для заданного порядка M и затухание боковых лепестков с равноволновой характеристикой в, используя полиномы Чебышёва. Изначально разработан Дольфом для оптимизации направленности радиоантенных решёток.
В отличие от большинства окон, окно Дольфа-Чебышёва определяется через свою частотную характеристику:
\[W(k) = \frac {\cos\{M \cos^{-1}[\beta \cos(\frac{\pi k}{M})]\}} {\cosh[M \cosh^{-1}(\beta)]}\]где
\[\beta = \cosh \left [\frac{1}{M} \cosh^{-1}(10^\frac{A}{20}) \right ]\]и 0 <= abs(k) <= M-1. A — затухание в децибелах (в).
Временное окно затем генерируется с использованием обратного БПФ, поэтому степени двойки M генерируются быстрее всего, а простые числа M являются самыми медленными.
Условие равнопульсации в частотной области создает импульсы во временной области, которые появляются на концах окна.
Ссылки
[1]C. Dolph, «A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level», Proceedings of the IEEE, Vol. 34, Issue 6
[2]Peter Lynch, “The Dolph-Chebyshev Window: A Simple Optimal Filter”, American Meteorological Society (April 1997) http://mathsci.ucd.ie/~plynch/Publications/Dolph.pdf
[3]Ф. Дж. Харрис, «Об использовании окон для гармонического анализа с дискретным преобразованием Фурье», Proceedings of the IEEE, Том 66, № 1, январь 1978
Примеры
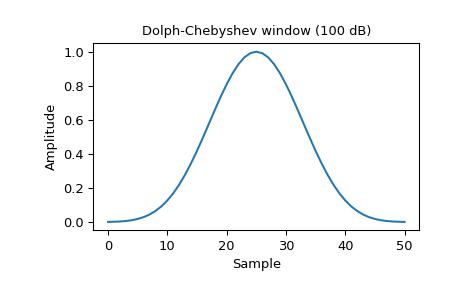
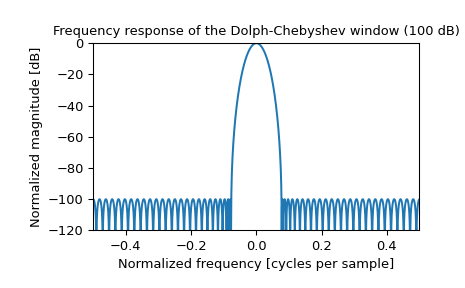
Построить окно и его частотную характеристику:
>>> import numpy as np >>> from scipy import signal >>> from scipy.fft import fft, fftshift >>> import matplotlib.pyplot as plt
>>> window = signal.windows.chebwin(51, at=100) >>> plt.plot(window) >>> plt.title("Dolph-Chebyshev window (100 dB)") >>> plt.ylabel("Amplitude") >>> plt.xlabel("Sample")
>>> plt.figure() >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max()))) >>> plt.plot(freq, response) >>> plt.axis([-0.5, 0.5, -120, 0]) >>> plt.title("Frequency response of the Dolph-Chebyshev window (100 dB)") >>> plt.ylabel("Normalized magnitude [dB]") >>> plt.xlabel("Normalized frequency [cycles per sample]")