scipy.signal.windows.

экспоненциальный

scipy.signal.windows.экспоненциальный(M, центр=None, tau=1.0, sym=True, *, xp=None, device=None)

Возвращает экспоненциальное (или пуассоновское) окно.

Параметры:

Mint

Первая строка матрицы. Если None,

центрfloat, опционально

Параметр, определяющий центральное положение оконной функции. Значение по умолчанию, если не указано, — center = (M-1) / 2. Этот параметр должен принимать значение по умолчанию для симметричных окон.

taufloat, опционально

Параметр, определяющий затухание. Для center = 0 использовать tau = -(M-1) / ln(x) if x это доля окна, оставшаяся в конце.

symbool, необязательно

Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.

xparray_namespace, опционально

Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию: numpy

устройство: любое

необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в xp.

Возвращает:

wndarray

Окно, с максимальным значением, нормализованным до 1 (хотя значение 1 не появляется, если M четно и sym равно True).

Примечания

Экспоненциальное окно определяется как

\[w(n) = e^{-|n-center| / \tau}\]

Ссылки

[1]

S. Gade и H. Herlufsen, «Окна для анализа БПФ (Часть I)», Technical Review 3, Bruel & Kjaer, 1987.

Примеры

Попробуйте в вашем браузере!

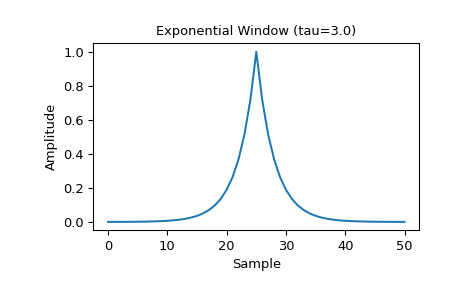
Постройте симметричное окно и его частотную характеристику:

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> M = 51
>>> tau = 3.0
>>> window = signal.windows.exponential(M, tau=tau)
>>> plt.plot(window)
>>> plt.title("Exponential Window (tau=3.0)")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

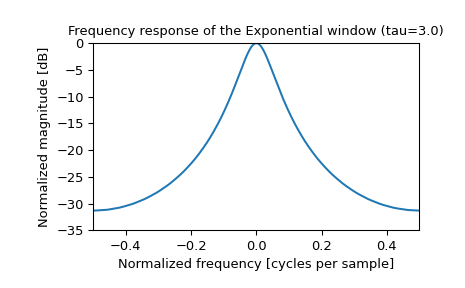
>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -35, 0])
>>> plt.title("Frequency response of the Exponential window (tau=3.0)")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

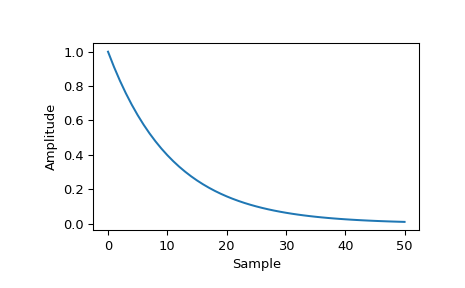
Эта функция также может генерировать несимметричные окна:

>>> tau2 = -(M-1) / np.log(0.01)
>>> window2 = signal.windows.exponential(M, 0, tau2, False)
>>> plt.figure()
>>> plt.plot(window2)
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

НазадОткрыть во вкладке