scipy.signal.windows.

general_cosine

scipy.signal.windows.general_cosine(M, a, sym=True)

Общее взвешенное суммирование косинусных членов окна

Параметры:

Mint

Количество точек в выходном окне

aarray_like

Последовательность весовых коэффициентов. Здесь используется соглашение о центрировании в начале координат, поэтому обычно все они будут положительными числами, а не чередующимися по знаку.

symbool, необязательно

Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.

Возвращает:

wndarray

Массив значений окна.

Ссылки

[1]

A. Nuttall, «Некоторые окна с очень хорошим поведением боковых лепестков», IEEE Transactions on Acoustics, Speech, and Signal Processing, т. 29, № 1, стр. 84-91, фев. 1981. DOI:10.1109/TASSP.1981.1163506.

[2]

Хайнцель Г. и др., «Оценка спектра и спектральной плотности с помощью дискретного преобразования Фурье (ДПФ), включая полный список оконных функций и некоторые новые окна с плоской вершиной», 15 февраля 2002 https://holometer.fnal.gov/GH_FFT.pdf

Примеры

Попробуйте в вашем браузере!

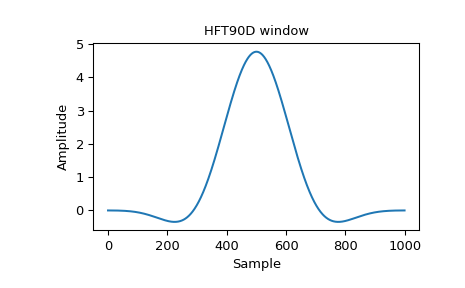
Heinzel описывает окно с плоской вершиной под названием "HFT90D" с формулой: [2]

\[w_j = 1 - 1.942604 \cos(z) + 1.340318 \cos(2z) - 0.440811 \cos(3z) + 0.043097 \cos(4z)\]

где

\[z = \frac{2 \pi j}{N}, j = 0...N - 1\]

Поскольку здесь используется соглашение о начале в начале координат, чтобы воспроизвести окно, нам нужно преобразовать каждый второй коэффициент в положительное число:

>>> HFT90D = [1, 1.942604, 1.340318, 0.440811, 0.043097]

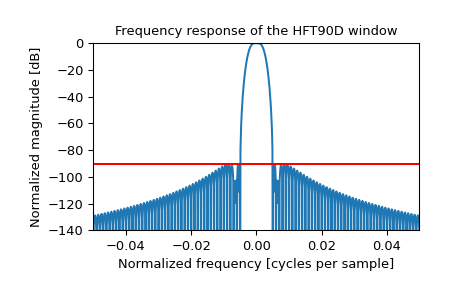
В статье указано, что самый высокий боковой лепесток находится на уровне -90.2 дБ. Воспроизведите Рисунок 42, построив окно и его частотную характеристику, и подтвердите уровень бокового лепестка красным цветом:

>>> import numpy as np
>>> from scipy.signal.windows import general_cosine
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = general_cosine(1000, HFT90D, sym=False)
>>> plt.plot(window)
>>> plt.title("HFT90D window")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

>>> plt.figure()
>>> A = fft(window, 10000) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = np.abs(fftshift(A / abs(A).max()))
>>> response = 20 * np.log10(np.maximum(response, 1e-10))
>>> plt.plot(freq, response)
>>> plt.axis([-50/1000, 50/1000, -140, 0])
>>> plt.title("Frequency response of the HFT90D window")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")
>>> plt.axhline(-90.2, color='red')
>>> plt.show()

НазадОткрыть во вкладке