scipy.signal.windows.

general_hamming

scipy.signal.windows.general_hamming(M, alpha, sym=True, *, xp=None, device=None)

Возвращает обобщённое окно Хэмминга.

Обобщённое окно Хэмминга строится путём умножения прямоугольного окна на один период косинусоидальной функции [1].

Параметры:

Mint

Первая строка матрицы. Если None,

alphafloat

Коэффициент окна, \(\alpha\)

symbool, необязательно

Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.

xparray_namespace, опционально

Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию: numpy

устройство: любое

необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в xp.

Возвращает:

wndarray

Окно, с максимальным значением, нормализованным до 1 (хотя значение 1 не появляется, если M четно и sym равно True).

Смотрите также

hamming, hann

Примечания

Обобщённое окно Хэмминга определяется как

\[w(n) = \alpha - \left(1 - \alpha\right) \cos\left(\frac{2\pi{n}}{M-1}\right) \qquad 0 \leq n \leq M-1\]

Как обычное окно Хэмминга, так и окно Ханна являются частными случаями обобщённого окна Хэмминга с \(\alpha\) = 0.54 и \(\alpha\) = 0.5 соответственно [2].

Ссылки

[1]

DSPRelated, “Generalized Hamming Window Family”, https://www.dsprelated.com/freebooks/sasp/Generalized_Hamming_Window_Family.html

[2]

Википедия, "Оконная функция", https://en.wikipedia.org/wiki/Window_function

[3]

Риккардо Пьянтанида ESA, "Sentinel-1 Level 1 Detailed Algorithm Definition", https://sentinel.esa.int/documents/247904/1877131/Sentinel-1-Level-1-Detailed-Algorithm-Definition

[4]

Matthieu Bourbigot ESA, "Sentinel-1 Product Definition", https://sentinel.esa.int/documents/247904/1877131/Sentinel-1-Product-Definition

Примеры

Попробуйте в вашем браузере!

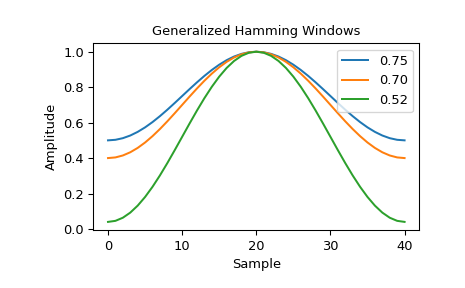
Обрабатывающая система инструментов Sentinel-1A/B использует обобщённые окна Хэмминга при обработке данных космической синтезированной апертурной радиолокации (SAR) [3]. Установка использует различные значения для \(\alpha\) параметр на основе режима работы SAR-инструмента. Некоторые распространенные \(\alpha\) значения включают 0.75, 0.7 и 0.52 [4]. В качестве примера мы строим графики этих различных окон.

>>> import numpy as np
>>> from scipy.signal.windows import general_hamming
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> fig1, spatial_plot = plt.subplots()
>>> spatial_plot.set_title("Generalized Hamming Windows")
>>> spatial_plot.set_ylabel("Amplitude")
>>> spatial_plot.set_xlabel("Sample")

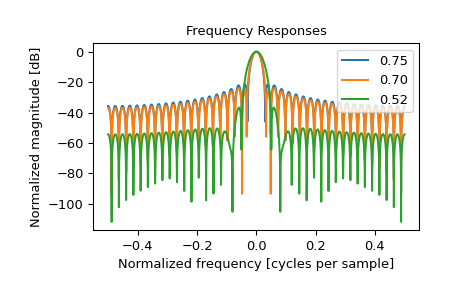
>>> fig2, freq_plot = plt.subplots()
>>> freq_plot.set_title("Frequency Responses")
>>> freq_plot.set_ylabel("Normalized magnitude [dB]")
>>> freq_plot.set_xlabel("Normalized frequency [cycles per sample]")

>>> for alpha in [0.75, 0.7, 0.52]:
...     window = general_hamming(41, alpha)
...     spatial_plot.plot(window, label="{:.2f}".format(alpha))
...     A = fft(window, 2048) / (len(window)/2.0)
...     freq = np.linspace(-0.5, 0.5, len(A))
...     response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
...     freq_plot.plot(freq, response, label="{:.2f}".format(alpha))
>>> freq_plot.legend(loc="upper right")
>>> spatial_plot.legend(loc="upper right")

НазадОткрыть во вкладке