kaiser#
- scipy.signal.windows.kaiser(M, beta, sym=True, *, xp=None, device=None)[источник]#
Возвращает окно Кайзера.
Окно Кайзера — это сужение, образованное с использованием функции Бесселя.
- Параметры:
- Mint
Первая строка матрицы. Если None,
- betafloat
Параметр формы, определяющий компромисс между шириной главного лепестка и уровнем боковых лепестков. При увеличении beta окно сужается.
- symbool, необязательно
Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.
- xparray_namespace, опционально
Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию:
numpy- устройство: любое
необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в
xp.
- Возвращает:
- wndarray
Окно, с максимальным значением, нормализованным до 1 (хотя значение 1 не появляется, если M четно и sym равно True).
Примечания
Окно Кайзера определяется как
\[w(n) = I_0\left( \beta \sqrt{1-\frac{4n^2}{(M-1)^2}} \right)/I_0(\beta)\]с
\[\quad -\frac{M-1}{2} \leq n \leq \frac{M-1}{2},\]где \(I_0\) является модифицированной функцией Бесселя нулевого порядка.
Окно Кайзера названо в честь Джима Кайзера, который обнаружил простое приближение к окну DPSS на основе функций Бесселя. Окно Кайзера - очень хорошее приближение к дискретной пролатной сфероидальной последовательности, или окну Слепиана, которое является преобразованием, максимизирующим энергию в главном лепестке окна относительно общей энергии.
Окно Кайзера может аппроксимировать другие окна, варьируя параметр beta. (В некоторых источниках используется alpha = beta/pi.) [4]
beta
Форма окна
0
Прямоугольный
5
Аналогично Хэммингу
6
Похоже на окно Ханна
8.6
Похож на Blackman
Значение beta, равное 14, вероятно, является хорошей отправной точкой. Обратите внимание, что по мере увеличения beta окно сужается, поэтому количество выборок должно быть достаточно большим, чтобы сэмплировать всё более узкий пик, иначе будут возвращены NaN.
Большинство ссылок на окно Кайзера происходят из литературы по обработке сигналов, где оно используется как одна из многих оконных функций для сглаживания значений. Оно также известно как аподизация (что означает «удаление ноги», т.е. сглаживание разрывов в начале и конце дискретизированного сигнала) или сужающая функция.
Ссылки
[1]J. F. Kaiser, "Цифровые фильтры" - Глава 7 в "Анализ систем с помощью цифрового компьютера", редакторы: F.F. Kuo и J.F. Kaiser, стр. 218-285. John Wiley and Sons, Нью-Йорк, (1966).
[2]E.R. Kanasewich, «Time Sequence Analysis in Geophysics», The University of Alberta Press, 1975, pp. 177-178.
[3]Википедия, "Оконная функция", https://en.wikipedia.org/wiki/Window_function
[4]F. J. Harris, “On the use of windows for harmonic analysis with the discrete Fourier transform,” Proceedings of the IEEE, vol. 66, no. 1, pp. 51-83, Jan. 1978. DOI:10.1109/PROC.1978.10837.
Примеры
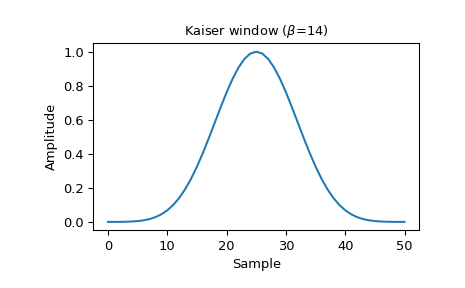
Построить окно и его частотную характеристику:
>>> import numpy as np >>> from scipy import signal >>> from scipy.fft import fft, fftshift >>> import matplotlib.pyplot as plt
>>> window = signal.windows.kaiser(51, beta=14) >>> plt.plot(window) >>> plt.title(r"Kaiser window ($\beta$=14)") >>> plt.ylabel("Amplitude") >>> plt.xlabel("Sample")
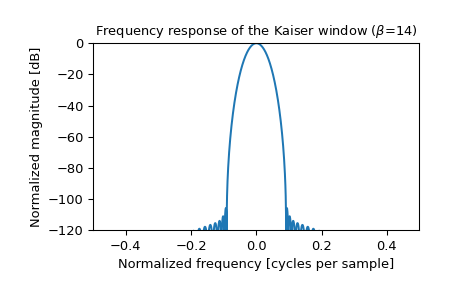
>>> plt.figure() >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max()))) >>> plt.plot(freq, response) >>> plt.axis([-0.5, 0.5, -120, 0]) >>> plt.title(r"Frequency response of the Kaiser window ($\beta$=14)") >>> plt.ylabel("Normalized magnitude [dB]") >>> plt.xlabel("Normalized frequency [cycles per sample]")