lanczos#
- scipy.signal.windows.lanczos(M, *, sym=True, xp=None, device=None)[источник]#
Вернуть окно Ланцоша, также известное как sinc-окно.
- Параметры:
- Mint
Первая строка матрицы. Если None,
- symbool, необязательно
Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.
- xparray_namespace, опционально
Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию:
numpy- устройство: любое
необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в
xp.
- Возвращает:
- wndarray
Окно, с максимальным значением, нормализованным до 1 (хотя значение 1 не появляется, если M четно и sym равно True).
Примечания
Окно Ланцоша определяется как
\[w(n) = sinc \left( \frac{2n}{M - 1} - 1 \right)\]где
\[sinc(x) = \frac{\sin(\pi x)}{\pi x}\]Окно Ланцоша имеет уменьшенные колебания Гиббса и широко используется для фильтрации климатических временных рядов с хорошими свойствами в физической и спектральной областях.
Добавлено в версии 1.10.
Ссылки
[1]Lanczos, C., and Teichmann, T. (1957). Applied analysis. Physics Today, 10, 44.
[2]Duchon C. E. (1979) Lanczos Filtering in One and Two Dimensions. Journal of Applied Meteorology, Vol 18, pp 1016-1022.
[3]Thomson, R. E. and Emery, W. J. (2014) Data Analysis Methods in Physical Oceanography (Third Edition), Elsevier, pp 593-637.
[4]Википедия, "Оконная функция", http://en.wikipedia.org/wiki/Window_function
Примеры
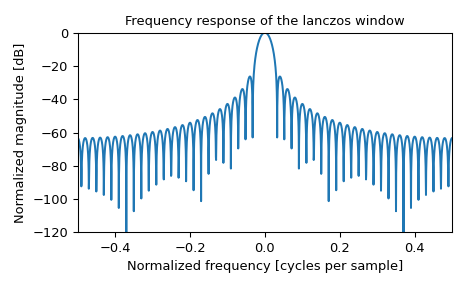
Построить окно
>>> import numpy as np >>> from scipy.signal.windows import lanczos >>> from scipy.fft import fft, fftshift >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots(1) >>> window = lanczos(51) >>> ax.plot(window) >>> ax.set_title("Lanczos window") >>> ax.set_ylabel("Amplitude") >>> ax.set_xlabel("Sample") >>> fig.tight_layout() >>> plt.show()
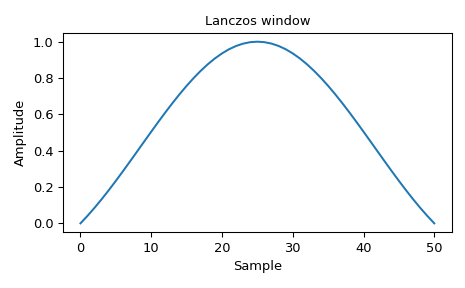
и его частотная характеристика:
>>> fig, ax = plt.subplots(1) >>> A = fft(window, 2048) / (len(window)/2.0) >>> freq = np.linspace(-0.5, 0.5, len(A)) >>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max()))) >>> ax.plot(freq, response) >>> ax.set_xlim(-0.5, 0.5) >>> ax.set_ylim(-120, 0) >>> ax.set_title("Frequency response of the lanczos window") >>> ax.set_ylabel("Normalized magnitude [dB]") >>> ax.set_xlabel("Normalized frequency [cycles per sample]") >>> fig.tight_layout() >>> plt.show()