scipy.signal.windows.

dpss#

scipy.signal.windows.dpss(M, NW, Kmax=None, sym=True, norm=None, return_ratios=False, *, xp=None, device=None)[источник]#

Вычислить дискретные пролатные сфероидальные последовательности (DPSS).

DPSS (или последовательности Слепяна) часто используются в многоленточной оценке спектральной плотности мощности (см. [1]). Первое окно в последовательности можно использовать для максимизации концентрации энергии в главном лепестке и также называется окном Слепяна.

Параметры:

Mint: Длина окна.
NWfloat: Стандартизированная половинная ширина полосы, соответствующая 2*NW = BW/f0 = BW*M*dt где dt принимается как 1.
Kmaxint | None, optional: Количество возвращаемых окон DPSS (порядки 0 через Kmax-1). Если None (по умолчанию), возвращается только одно окно формы (M,) вместо массива окон формы (Kmax, M).
symbool, необязательно: Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.
norm{2, 'approximate', 'subsample'} | None, optional: Если 'approximate' или 'subsample', то окна нормализуются по максимуму, и применяется поправочный масштабный коэффициент для окон четной длины, используя M**2/(M**2+NW) («приблизительный») или сдвиг на основе БПФ с субдискретизацией («subsample»), подробности см. в примечаниях. Если None, то «приблизительный» используется, когда Kmax=None и 2 в противном случае (что использует норму l2).
return_ratiosbool, необязательно: Если True, также возвращает коэффициенты концентрации в дополнение к окнам.
xparray_namespace, опционально: Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию: numpy
устройство: любое: необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в xp.

Возвращает:

vndarray, форма (Kmax, M) или (M,): Окна DPSS. Будет одномерным, если Kmax равно None.
rndarray, форма (Kmax,) или float, опционально: Коэффициенты концентрации для окон. Возвращается только если return_ratios вычисляется как True. Будет 0D, если Kmax равно None.

Примечания

Это вычисление использует тридиагональную формулировку собственных векторов, приведённую в [2].

Нормализация по умолчанию для Kmax=None, т.е. режим генерации окна, простое использование l-бесконечной нормы создаст окно с двумя единичными значениями, что приводит к небольшим различиям в нормировке между чётными и нечётными порядками. Приблизительная коррекция M**2/float(M**2+NW) для чётных номеров выборок используется для противодействия этому эффекту (см. примеры ниже).

Для очень длинных сигналов (например, 1e6 элементов) может быть полезно вычислять окна на порядки короче и использовать интерполяцию (например, scipy.interpolate.interp1d) для получения сужений длиной M, но это в общем случае не сохранит ортогональность между тейперами.

Добавлено в версии 1.1.

Ссылки

[1]

Персиваль Д.Б., Уолден У.Т. Спектральный анализ для физических приложений: Многоленточные и традиционные одномерные методы. Издательство Кембриджского университета; 1993.

[2]

Slepian, D. Prolate spheroidal wave functions, Fourier analysis, and uncertainty V: The discrete case. Bell System Technical Journal, Volume 57 (1978), 1371430.

[3]

Kaiser, JF, Schafer RW. On the Use of the I0-Sinh Window for Spectrum Analysis. IEEE Transactions on Acoustics, Speech and Signal Processing. ASSP-28 (1): 105-107; 1980.

Примеры

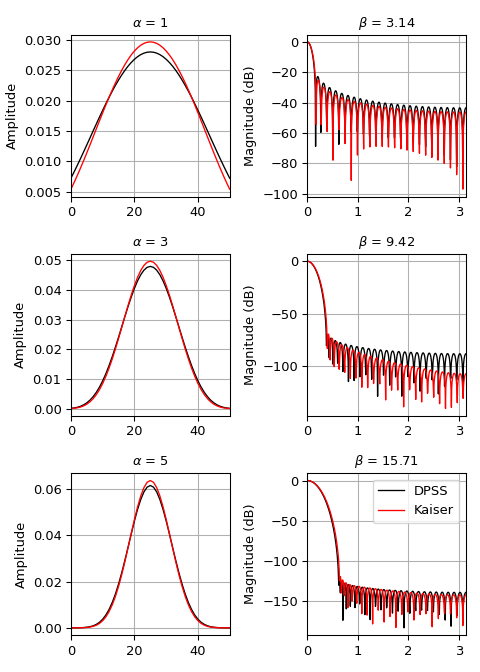
Мы можем сравнить окно с kaiser, который был изобретен как альтернатива, более простая для вычисления [3] (пример адаптирован из здесь):

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import windows, freqz
>>> M = 51
>>> fig, axes = plt.subplots(3, 2, figsize=(5, 7))
>>> for ai, alpha in enumerate((1, 3, 5)):
...     win_dpss = windows.dpss(M, alpha)
...     beta = alpha*np.pi
...     win_kaiser = windows.kaiser(M, beta)
...     for win, c in ((win_dpss, 'k'), (win_kaiser, 'r')):
...         win /= win.sum()
...         axes[ai, 0].plot(win, color=c, lw=1.)
...         axes[ai, 0].set(xlim=[0, M-1], title=rf'$\alpha$ = {alpha}',
...                         ylabel='Amplitude')
...         w, h = freqz(win)
...         axes[ai, 1].plot(w, 20 * np.log10(np.abs(h)), color=c, lw=1.)
...         axes[ai, 1].set(xlim=[0, np.pi],
...                         title=rf'$\beta$ = {beta:0.2f}',
...                         ylabel='Magnitude (dB)')
>>> for ax in axes.ravel():
...     ax.grid(True)
>>> axes[2, 1].legend(['DPSS', 'Kaiser'])
>>> fig.tight_layout()
>>> plt.show()

../../_images/scipy-signal-windows-dpss-1_00_00.png

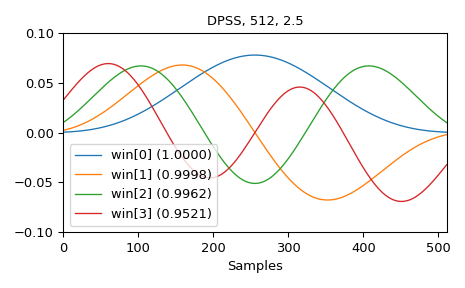
А вот примеры первых четырёх окон вместе с их коэффициентами концентрации:

>>> M = 512
>>> NW = 2.5
>>> win, eigvals = windows.dpss(M, NW, 4, return_ratios=True)
>>> fig, ax = plt.subplots(1)
>>> ax.plot(win.T, linewidth=1.)
>>> ax.set(xlim=[0, M-1], ylim=[-0.1, 0.1], xlabel='Samples',
...        title=f'DPSS, {M:d}, {NW:0.1f}')
>>> ax.legend([f'win[{ii}] ({ratio:0.4f})'
...            for ii, ratio in enumerate(eigvals)])
>>> fig.tight_layout()
>>> plt.show()

../../_images/scipy-signal-windows-dpss-1_01_00.png

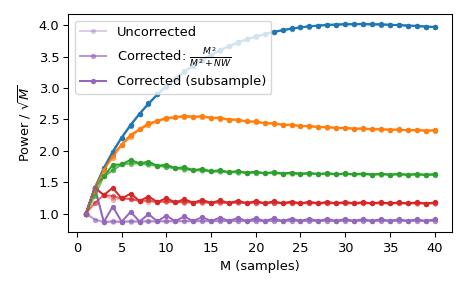
Используя стандартный \(l_{\infty}\) norm даст два единичных значения для чётных M, но только одно единичное значение для нечётных M. Это создает неравномерную мощность окна, которую можно компенсировать приблизительной коррекцией M**2/float(M**2+NW), который можно выбрать с помощью norm='approximate' (что совпадает с norm=None когда Kmax=None, как в данном случае). Альтернативно, более медленный norm='subsample' может использоваться, который использует сдвиг подвыборки в частотной области (БПФ) для вычисления поправки:

>>> Ms = np.arange(1, 41)
>>> factors = (50, 20, 10, 5, 2.0001)
>>> energy = np.empty((3, len(Ms), len(factors)))
>>> for mi, M in enumerate(Ms):
...     for fi, factor in enumerate(factors):
...         NW = M / float(factor)
...         # Corrected using empirical approximation (default)
...         win = windows.dpss(M, NW)
...         energy[0, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
...         # Corrected using subsample shifting
...         win = windows.dpss(M, NW, norm='subsample')
...         energy[1, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
...         # Uncorrected (using l-infinity norm)
...         win /= win.max()
...         energy[2, mi, fi] = np.sum(win ** 2) / np.sqrt(M)
>>> fig, ax = plt.subplots(1)
>>> hs = ax.plot(Ms, energy[2], '-o', markersize=4,
...              markeredgecolor='none')
>>> leg = [hs[-1]]
>>> for hi, hh in enumerate(hs):
...     h1 = ax.plot(Ms, energy[0, :, hi], '-o', markersize=4,
...                  color=hh.get_color(), markeredgecolor='none',
...                  alpha=0.66)
...     h2 = ax.plot(Ms, energy[1, :, hi], '-o', markersize=4,
...                  color=hh.get_color(), markeredgecolor='none',
...                  alpha=0.33)
...     if hi == len(hs) - 1:
...         leg.insert(0, h1[0])
...         leg.insert(0, h2[0])
>>> ax.set(xlabel='M (samples)', ylabel=r'Power / $\sqrt{M}$')
>>> ax.legend(leg, ['Uncorrected', r'Corrected: $\frac{M^2}{M^2+NW}$',
...                 'Corrected (subsample)'])
>>> fig.tight_layout()

../../_images/scipy-signal-windows-dpss-1_02_00.png