scipy.spatial.transform.

RotationSpline

класс scipy.spatial.transform.RotationSpline(раз, вращения)

Интерполяция вращений с непрерывной угловой скоростью и ускорением.

Векторы вращения между каждой последовательной ориентацией являются кубическими функциями времени, и гарантируется, что угловая скорость и ускорение непрерывны. Такая интерполяция аналогична кубической сплайн- интерполяции.

См. [1] для математических и реализационных деталей.

Параметры:

разarray_like, shape (N,)

Времена известных вращений. Должно быть указано не менее 2 времен.

вращенияRotation экземпляр

Вращения для выполнения интерполяции между ними. Должны содержать N вращений.

Методы

__call__(times[, order])

Вычислить интерполированные значения.

Ссылки

[1]

Плавная интерполяция ориентации

Примеры

Попробуйте в вашем браузере!

>>> from scipy.spatial.transform import Rotation, RotationSpline
>>> import numpy as np

Определить последовательность времен и вращений из углов Эйлера:

>>> times = [0, 10, 20, 40]
>>> angles = [[-10, 20, 30], [0, 15, 40], [-30, 45, 30], [20, 45, 90]]
>>> rotations = Rotation.from_euler('XYZ', angles, degrees=True)

Создать объект интерполятора:

>>> spline = RotationSpline(times, rotations)

Интерполировать углы Эйлера, угловую скорость и ускорение:

>>> angular_rate = np.rad2deg(spline(times, 1))
>>> angular_acceleration = np.rad2deg(spline(times, 2))
>>> times_plot = np.linspace(times[0], times[-1], 100)
>>> angles_plot = spline(times_plot).as_euler('XYZ', degrees=True)
>>> angular_rate_plot = np.rad2deg(spline(times_plot, 1))
>>> angular_acceleration_plot = np.rad2deg(spline(times_plot, 2))

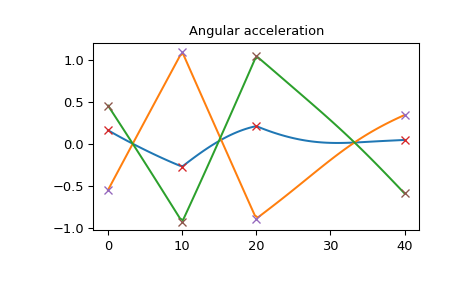
На этом графике видно, что углы Эйлера непрерывны и гладки:

>>> import matplotlib.pyplot as plt
>>> plt.plot(times_plot, angles_plot)
>>> plt.plot(times, angles, 'x')
>>> plt.title("Euler angles")
>>> plt.show()

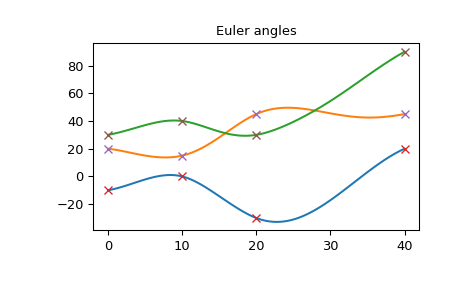
Угловая скорость также плавная:

>>> plt.plot(times_plot, angular_rate_plot)
>>> plt.plot(times, angular_rate, 'x')
>>> plt.title("Angular rate")
>>> plt.show()

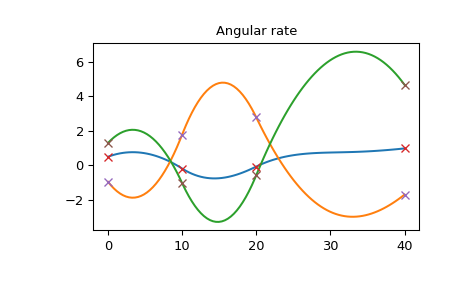
Угловое ускорение непрерывно, но не гладко. Также обратите внимание, что угловое ускорение не является кусочно-линейной функцией, потому что оно отличается от второй производной вектора вращения (которая является кусочно-линейной функцией, как в кубическом сплайне).

>>> plt.plot(times_plot, angular_acceleration_plot)
>>> plt.plot(times, angular_acceleration, 'x')
>>> plt.title("Angular acceleration")
>>> plt.show()

НазадОткрыть во вкладке