scipy.spatial.transform.

Вращение#

класс scipy.spatial.transform.Вращение#

Вращение в 3-х измерениях.

Этот класс предоставляет интерфейс для инициализации и представления вращений с помощью:

Кватернионы
Матрицы вращения
Векторы вращения
Модифицированные параметры Родригеса
Углы Эйлера
Углы Дэвенпорта (Обобщённые углы Эйлера)

Следующие операции с вращениями поддерживаются:

Применение к векторам
Композиция вращений
Инверсия вращения
Индексация вращения

Индексирование внутри вращения поддерживается, так как несколько преобразований вращения могут храниться в одном Rotation экземпляр.

Чтобы создать Rotation объекты используют from_... методы (см. примеры ниже). Rotation(...) не предназначен для непосредственного создания экземпляра.

Атрибуты:

single: Представляет ли этот экземпляр одно вращение.

Методы

`__len__`(self)	Количество вращений, содержащихся в этом объекте.
`from_quat`(cls, quat, *[, scalar_first])	Инициализация из кватернионов.
`from_matrix`(cls, matrix)	Инициализировать из матрицы вращения.
`from_rotvec`(cls, rotvec[, degrees])	Инициализация из векторов вращения.
`from_mrp`(cls, mrp)	Инициализация из модифицированных параметров Родригеса (MRPs).
`from_euler`(cls, seq, angles[, degrees])	Инициализация из углов Эйлера.
`from_davenport`(cls, axes, order, angles[, ...])	Инициализировать из углов Дэвенпорта.
`as_quat`(self[, canonical, scalar_first])	Представить в виде кватернионов.
`as_matrix`(self)	Представить как матрицу вращения.
`as_rotvec`(self[, degrees])	Представить как векторы вращения.
`as_mrp`(self)	Представить как модифицированные параметры Родригеса (MRPs).
`as_euler`(self, seq[, degrees])	Представить в виде углов Эйлера.
`as_davenport`(self, axes, order[, degrees])	Представить как углы Дэвенпорта.
`concatenate`(cls, rotations)	Объединить последовательность `Rotation` объектов в единый объект.
`apply`(self, vectors[, inverse])	Применить это вращение к набору векторов.
`__mul__`(self, Rotation other)	Скомбинируйте это вращение с другим.
`__pow__`(self, float n, modulus)	Скомбинировать это вращение с самим собой n раз.
`inv`(self)	Инвертировать это вращение.
`magnitude`(self)	Получить величину(ы) вращения(ий).
`approx_equal`(self, Rotation other[, atol, ...])	Определить, приблизительно ли равен другой поворот данному.
`mean`(self[, weights])	Получить среднее значение вращений.
`reduce`(self[, left, right, return_indices])	Уменьшите это вращение с помощью предоставленных групп вращений.
`create_group`(cls, group[, axis])	Создать группу 3D-вращений.
`__getitem__`(self, indexer)	Извлечение вращения(ий) по заданному(ым) индексу(ам) из объекта.
`identity`(cls[, num])	Получить тождественное вращение(я).
`random`(cls[, num, rng])	Генерировать равномерно распределенные вращения.
`align_vectors`(cls, a, b[, weights, ...])	Оценить вращение для оптимального выравнивания двух наборов векторов.

Смотрите также

Slerp

Примечания

Добавлено в версии 1.2.0.

Примеры

>>> from scipy.spatial.transform import Rotation as R
>>> import numpy as np

A Rotation Экземпляр может быть инициализирован в любом из вышеуказанных форматов и преобразован в любой другой. Базовый объект не зависит от представления, используемого для инициализации.

Рассмотрим вращение на 90 градусов против часовой стрелки вокруг оси z. Это соответствует следующему кватерниону (в формате скаляр-последний):

>>> r = R.from_quat([0, 0, np.sin(np.pi/4), np.cos(np.pi/4)])

Вращение может быть выражено в любом из других форматов:

>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
[ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
[ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

Та же самая ротация может быть инициализирована с использованием матрицы вращения:

>>> r = R.from_matrix([[0, -1, 0],
...                    [1, 0, 0],
...                    [0, 0, 1]])

Представление в других форматах:

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

Вектор вращения, соответствующий этому вращению, задается как:

>>> r = R.from_rotvec(np.pi/2 * np.array([0, 0, 1]))

Представление в других форматах:

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

The from_euler метод довольно гибкий в диапазоне поддерживаемых форматов входных данных. Здесь мы инициализируем одно вращение вокруг одной оси:

>>> r = R.from_euler('z', 90, degrees=True)

Опять же, объект не зависит от представления и может быть преобразован в любой другой формат:

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])

Также возможно инициализировать несколько вращений в одном экземпляре с использованием любого из from_... функций. Здесь мы инициализируем стек из 3 вращений, используя from_euler method:

>>> r = R.from_euler('zyx', [
... [90, 0, 0],
... [0, 45, 0],
... [45, 60, 30]], degrees=True)

Другие представления теперь также возвращают стек из 3 вращений. Например:

>>> r.as_quat()
array([[0.        , 0.        , 0.70710678, 0.70710678],
       [0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])

Применение указанных вращений к вектору:

>>> v = [1, 2, 3]
>>> r.apply(v)
array([[-2.        ,  1.        ,  3.        ],
       [ 2.82842712,  2.        ,  1.41421356],
       [ 2.24452282,  0.78093109,  2.89002836]])

A Rotation экземпляр может быть проиндексирован и нарезан, как если бы это был один 1D массив или список:

>>> r.as_quat()
array([[0.        , 0.        , 0.70710678, 0.70710678],
       [0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])
>>> p = r[0]
>>> p.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> q = r[1:3]
>>> q.as_quat()
array([[0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])

Фактически его можно преобразовать в numpy.array:

>>> r_array = np.asarray(r)
>>> r_array.shape
(3,)
>>> r_array[0].as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])

Несколько вращений могут быть скомпонованы с использованием * оператор:

>>> r1 = R.from_euler('z', 90, degrees=True)
>>> r2 = R.from_rotvec([np.pi/4, 0, 0])
>>> v = [1, 2, 3]
>>> r2.apply(r1.apply(v))
array([-2.        , -1.41421356,  2.82842712])
>>> r3 = r2 * r1 # Note the order
>>> r3.apply(v)
array([-2.        , -1.41421356,  2.82842712])

Вращение может быть составлено с самим собой с помощью ** оператор:

>>> p = R.from_rotvec([1, 0, 0])
>>> q = p ** 2
>>> q.as_rotvec()
array([2., 0., 0.])

Наконец, также возможно инвертировать вращения:

>>> r1 = R.from_euler('z', [90, 45], degrees=True)
>>> r2 = r1.inv()
>>> r2.as_euler('zyx', degrees=True)
array([[-90.,   0.,   0.],
       [-45.,   0.,   0.]])

Следующая функция может использоваться для построения вращений с помощью Matplotlib, показывая, как они преобразуют стандартные оси координат x, y, z:

>>> import matplotlib.pyplot as plt

>>> def plot_rotated_axes(ax, r, name=None, offset=(0, 0, 0), scale=1):
...     colors = ("#FF6666", "#005533", "#1199EE")  # Colorblind-safe RGB
...     loc = np.array([offset, offset])
...     for i, (axis, c) in enumerate(zip((ax.xaxis, ax.yaxis, ax.zaxis),
...                                       colors)):
...         axlabel = axis.axis_name
...         axis.set_label_text(axlabel)
...         axis.label.set_color(c)
...         axis.line.set_color(c)
...         axis.set_tick_params(colors=c)
...         line = np.zeros((2, 3))
...         line[1, i] = scale
...         line_rot = r.apply(line)
...         line_plot = line_rot + loc
...         ax.plot(line_plot[:, 0], line_plot[:, 1], line_plot[:, 2], c)
...         text_loc = line[1]*1.2
...         text_loc_rot = r.apply(text_loc)
...         text_plot = text_loc_rot + loc[0]
...         ax.text(*text_plot, axlabel.upper(), color=c,
...                 va="center", ha="center")
...     ax.text(*offset, name, color="k", va="center", ha="center",
...             bbox={"fc": "w", "alpha": 0.8, "boxstyle": "circle"})

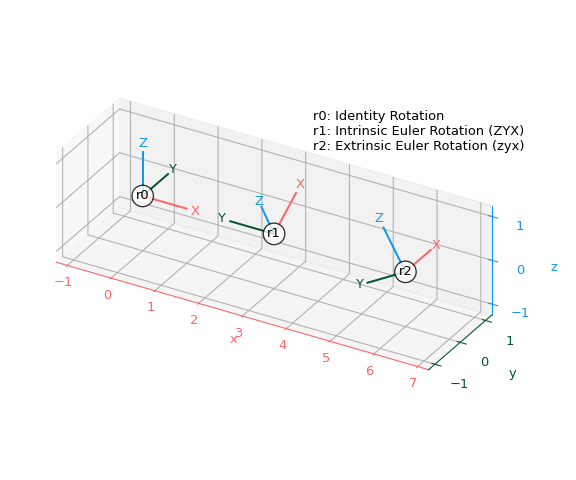
Создать три вращения — тождественное и два вращения Эйлера с использованием внутренних и внешних соглашений:

>>> r0 = R.identity()
>>> r1 = R.from_euler("ZYX", [90, -30, 0], degrees=True)  # intrinsic
>>> r2 = R.from_euler("zyx", [90, -30, 0], degrees=True)  # extrinsic

Добавьте все три вращения на один график:

>>> ax = plt.figure().add_subplot(projection="3d", proj_type="ortho")
>>> plot_rotated_axes(ax, r0, name="r0", offset=(0, 0, 0))
>>> plot_rotated_axes(ax, r1, name="r1", offset=(3, 0, 0))
>>> plot_rotated_axes(ax, r2, name="r2", offset=(6, 0, 0))
>>> _ = ax.annotate(
...     "r0: Identity Rotation\n"
...     "r1: Intrinsic Euler Rotation (ZYX)\n"
...     "r2: Extrinsic Euler Rotation (zyx)",
...     xy=(0.6, 0.7), xycoords="axes fraction", ha="left"
... )
>>> ax.set(xlim=(-1.25, 7.25), ylim=(-1.25, 1.25), zlim=(-1.25, 1.25))
>>> ax.set(xticks=range(-1, 8), yticks=[-1, 0, 1], zticks=[-1, 0, 1])
>>> ax.set_aspect("equal", adjustable="box")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.tight_layout()

Показать график:

>>> plt.show()

../../_images/scipy-spatial-transform-Rotation-1_00_00.png

Эти примеры служат обзором Rotation класс и выделить основные функциональные возможности. Для более подробных примеров диапазона поддерживаемых входных и выходных форматов обратитесь к примерам отдельных методов.