Трансляция (Broadcasting)#
Смотрите также
Термин трансляция описывает, как NumPy обрабатывает массивы с разными формами во время арифметических операций. При соблюдении определённых ограничений, меньший массив "транслируется" по большему массиву, чтобы они имели совместимые формы. Трансляция предоставляет средства векторизации операций с массивами, так что циклы выполняются на C вместо Python. Это делается без создания ненужных копий данных и обычно приводит к эффективным реализациям алгоритмов. Однако бывают случаи, когда трансляция является плохой идеей, потому что приводит к неэффективному использованию памяти, что замедляет вычисления.
Операции NumPy обычно выполняются над парами массивов поэлементно. В простейшем случае два массива должны иметь точно такую же форму, как в следующем примере:
>>> import numpy as np
>>> a = np.array([1.0, 2.0, 3.0])
>>> b = np.array([2.0, 2.0, 2.0])
>>> a * b
array([2., 4., 6.])
Правило вещания NumPy ослабляет это ограничение, когда формы массивов удовлетворяют определенным условиям. Простейший пример вещания возникает, когда массив и скалярное значение объединяются в операции:
>>> import numpy as np
>>> a = np.array([1.0, 2.0, 3.0])
>>> b = 2.0
>>> a * b
array([2., 4., 6.])
Результат эквивалентен предыдущему примеру, где b был массивом.
Мы можем рассматривать скаляр b будучи растянутый во время арифметической
операции в массив с той же формой, что и a. Новые элементы в
b, как показано в Рисунок 1, являются просто копиями
исходного скаляра. Аналогия с растяжением
только концептуальна. NumPy достаточно умен, чтобы использовать исходное скалярное значение
без фактического создания копий, чтобы операции вещания были максимально
эффективны по памяти и вычислениям.
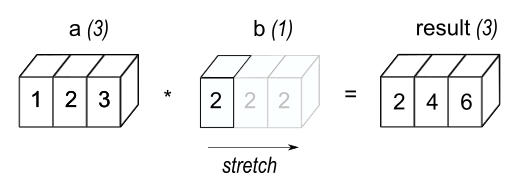
Рисунок 1#
В простейшем примере broadcasting, скаляр b растягивается, чтобы стать массивом той же формы, что и a так что формы совместимы для поэлементного умножения.
Код во втором примере более эффективен, чем в первом, потому что при умножении broadcasting перемещает меньше памяти (b является скаляром, а не массивом).
Общие правила трансляции (broadcasting)#
При работе с двумя массивами NumPy сравнивает их формы поэлементно. Начинается с последнего (т.е. самого правого) измерения и движется влево. Два измерения совместимы, когда
они равны, или
один из них равен 1.
Если эти условия не выполняются,
ValueError: operands could not be broadcast together выбрасывается исключение, указывающее, что массивы имеют несовместимые формы.
Входные массивы не обязательно должны иметь одинаковый число измерений. Результирующий массив будет иметь то же количество измерений, что и входной массив с наибольшим количеством измерений, где размер каждого измерения — это наибольший размер соответствующего измерения среди входных массивов. Обратите внимание, что отсутствующие измерения считаются имеющими размер один.
Например, если у вас есть 256x256x3 массив значений RGB, и вы хотите масштабировать каждый цвет в изображении на разное значение, вы можете умножить изображение на одномерный массив с 3 значениями. Согласование размеров конечных осей этих массивов согласно правилам трансляции показывает, что они совместимы:
Image (3d array): 256 x 256 x 3
Scale (1d array): 3
Result (3d array): 256 x 256 x 3
Когда любое из сравниваемых измерений равно единице, используется другое. Другими словами, измерения с размером 1 растягиваются или "копируются" для соответствия другому.
В следующем примере оба A и B массивы имеют оси с длиной один, которые расширяются до большего размера во время операции вещания:
A (4d array): 8 x 1 x 6 x 1
B (3d array): 7 x 1 x 5
Result (4d array): 8 x 7 x 6 x 5
Массивы, поддерживающие трансляцию#
Набор массивов называется "broadcastable" к одной форме, если вышеуказанные правила дают допустимый результат.
Например, если a.shape равно (5,1), b.shape равно (1,6), c.shape равен (6,)
и d.shape является (), так что d является скаляром, то a, b, c,
и d все могут быть транслированы до размерности (5,6); и
a ведёт себя как массив (5,6), где
a[:,0]транслируется на другие столбцы,b ведёт себя как массив (5,6), где
b[0,:]транслируется на другие строки,c ведёт себя как массив (1,6) и, следовательно, как массив (5,6), где
c[:]транслируется на каждую строку, и, наконец,d ведёт себя как массив (5,6), где единственное значение повторяется.
Вот еще несколько примеров:
A (2d array): 5 x 4
B (1d array): 1
Result (2d array): 5 x 4
A (2d array): 5 x 4
B (1d array): 4
Result (2d array): 5 x 4
A (3d array): 15 x 3 x 5
B (3d array): 15 x 1 x 5
Result (3d array): 15 x 3 x 5
A (3d array): 15 x 3 x 5
B (2d array): 3 x 5
Result (3d array): 15 x 3 x 5
A (3d array): 15 x 3 x 5
B (2d array): 3 x 1
Result (3d array): 15 x 3 x 5
Вот примеры форм, которые не вещают:
A (1d array): 3
B (1d array): 4 # trailing dimensions do not match
A (2d array): 2 x 1
B (3d array): 8 x 4 x 3 # second from last dimensions mismatched
Пример вещания, когда одномерный массив добавляется к двумерному массиву:
>>> import numpy as np
>>> a = np.array([[ 0.0, 0.0, 0.0],
... [10.0, 10.0, 10.0],
... [20.0, 20.0, 20.0],
... [30.0, 30.0, 30.0]])
>>> b = np.array([1.0, 2.0, 3.0])
>>> a + b
array([[ 1., 2., 3.],
[11., 12., 13.],
[21., 22., 23.],
[31., 32., 33.]])
>>> b = np.array([1.0, 2.0, 3.0, 4.0])
>>> a + b
Traceback (most recent call last):
ValueError: operands could not be broadcast together with shapes (4,3) (4,)
Как показано в Рисунок 2, b добавляется к каждой строке a.
В Рисунок 3, возникает исключение из-за несовместимых форм.
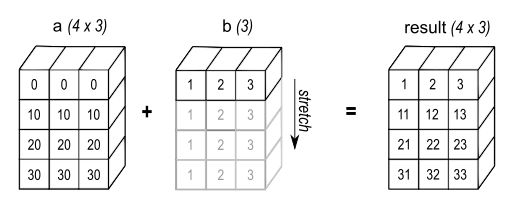
Рисунок 2#
Одномерный массив, добавленный к двумерному массиву, приводит к трансляции, если количество элементов одномерного массива совпадает с количеством столбцов двумерного массива.
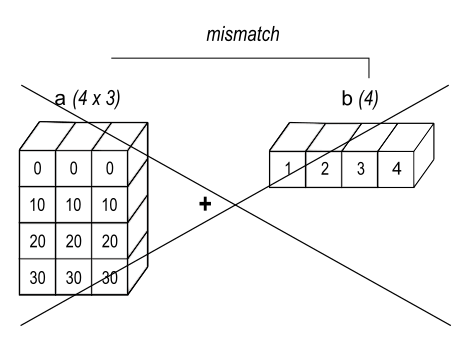
Рисунок 3#
Когда конечные размеры массивов не равны, трансляция не удается, потому что невозможно выровнять значения в строках первого массива с элементами второго массива для поэлементного сложения.
Трансляция предоставляет удобный способ взятия внешнего произведения (или любой другой внешней операции) двух массивов. Следующий пример показывает операцию внешнего сложения двух одномерных массивов:
>>> import numpy as np
>>> a = np.array([0.0, 10.0, 20.0, 30.0])
>>> b = np.array([1.0, 2.0, 3.0])
>>> a[:, np.newaxis] + b
array([[ 1., 2., 3.],
[11., 12., 13.],
[21., 22., 23.],
[31., 32., 33.]])
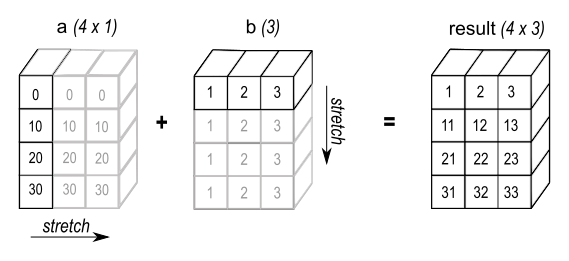
Рисунок 4#
В некоторых случаях вещание растягивает оба массива, чтобы сформировать выходной массив больший, чем любой из исходных массивов.
Здесь newaxis оператор индекса вставляет новую ось в a, делая его двумерным 4x1 массив. Объединение 4x1 массив
с b, который имеет форму (3,), возвращает 4x3 массив.
Практический пример: векторное квантование#
Трансляция (broadcasting) часто встречается в реальных задачах. Типичный пример
возникает в алгоритме векторного квантования (VQ), используемом в теории информации,
классификации и других смежных областях. Основная операция в VQ находит
ближайшую точку в наборе точек, называемом codes в терминологии VQ, к данной
точке, называемой observation. В очень простом двумерном случае,
показанном ниже, значения в observation описывают вес и рост спортсмена для классификации. The codes представляют различные классы
спортсменов. [1] Поиск ближайшей точки требует вычисления расстояния
между наблюдением и каждым из кодов. Кратчайшее расстояние дает
лучшее соответствие. В этом примере codes[0] является ближайшим классом, указывающим, что спортсмен, вероятно, баскетболист.
>>> from numpy import array, argmin, sqrt, sum
>>> observation = array([111.0, 188.0])
>>> codes = array([[102.0, 203.0],
... [132.0, 193.0],
... [45.0, 155.0],
... [57.0, 173.0]])
>>> diff = codes - observation # the broadcast happens here
>>> dist = sqrt(sum(diff**2,axis=-1))
>>> argmin(dist)
0
В этом примере observation массив растягивается, чтобы соответствовать форме codes массив:
Observation (1d array): 2
Codes (2d array): 4 x 2
Diff (2d array): 4 x 2
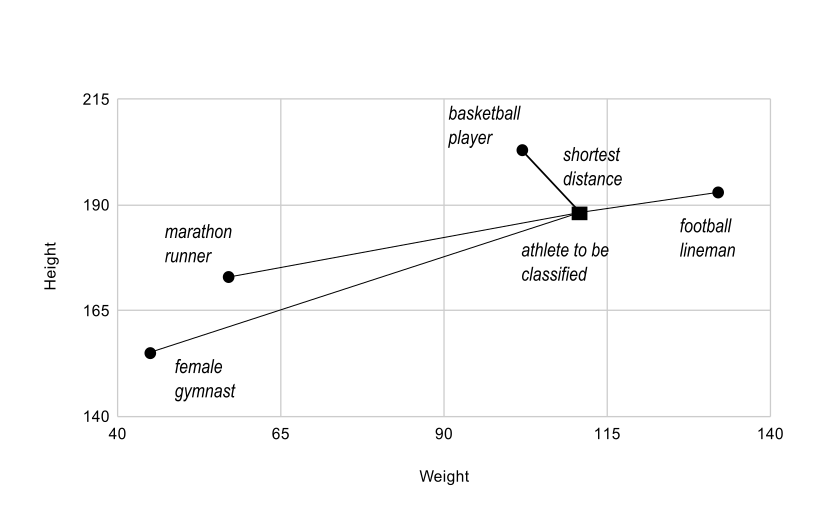
Рисунок 5#
Базовая операция векторного квантования вычисляет расстояние между объектом, который нужно классифицировать (тёмный квадрат), и несколькими известными кодами (серые круги). В этом простом случае коды представляют отдельные классы. Более сложные случаи используют несколько кодов на класс.
Обычно большое количество observations, возможно, считанные из базы данных,
сравниваются с набором codesРассмотрим этот сценарий:
Observation (2d array): 10 x 3
Codes (3d array): 5 x 1 x 3
Diff (3d array): 5 x 10 x 3
Трёхмерный массив, diff, является следствием трансляции, а не необходимостью для вычисления. Большие наборы данных будут генерировать большой промежуточный массив, который вычислительно неэффективен. Вместо этого, если каждое наблюдение вычисляется индивидуально с использованием цикла Python вокруг кода в двумерном примере выше, используется гораздо меньший массив.
Трансляция (broadcasting) — это мощный инструмент для написания короткого и обычно интуитивно понятного кода, который выполняет вычисления очень эффективно на C. Однако бывают случаи, когда трансляция использует неоправданно большие объемы памяти для конкретного алгоритма. В таких случаях лучше написать внешний цикл алгоритма на Python. Это также может сделать код более читаемым, поскольку алгоритмы, использующие трансляцию, становятся все труднее для интерпретации с увеличением количества измерений в трансляции.
Сноски