Быстрый старт NumPy#
Предварительные требования#
Вам потребуются базовые знания Python. Для повторения см. Python tutorial.
Для работы с примерами вам понадобится matplotlib установлен
в дополнение к NumPy.
Профиль обучающегося
Это краткий обзор массивов в NumPy. Он демонстрирует, как n-мерные\(n>=2\)) массивы представлены и могут быть обработаны. В частности, если вы не знаете, как применять общие функции к n-мерным массивам (без использования циклов for), или если вы хотите понять свойства оси и формы для n-мерных массивов, эта статья может помочь.
Цели обучения
После прочтения вы должны уметь:
Поймите разницу между одномерными, двумерными и n-мерными массивами в NumPy;
Понять, как применять некоторые операции линейной алгебры к n-мерным массивам без использования циклов for;
Понимание свойств axis и shape для n-мерных массивов.
Основы#
Основным объектом NumPy является однородный многомерный массив. Это таблица элементов (обычно чисел), все одного типа, индексируемая кортежем неотрицательных целых чисел. В NumPy измерения называются оси.
Например, массив для координат точки в 3D-пространстве,
[1, 2, 1], имеет одну ось. Эта ось содержит 3 элемента, поэтому мы говорим, что она имеет длину 3. В примере, изображенном ниже, массив имеет 2 оси. Первая ось имеет длину 2, вторая ось имеет длину 3.
[[1., 0., 0.],
[0., 1., 2.]]
Класс массива NumPy называется ndarray. Также известен под псевдонимом
array. Обратите внимание, что numpy.array не совпадает со стандартным
классом библиотеки Python array.array, который обрабатывает только одномерные
массивы и предлагает меньше функциональности. Более важные атрибуты
ndarray объекта:
- ndarray.ndim
количество осей (измерений) массива.
- ndarray.shape
размеры массива. Это кортеж целых чисел, указывающий размер массива в каждом измерении. Для матрицы с n строки и m столбцы,
shapeбудет(n,m). Длинаshapeкортеж, следовательно, представляет количество осей,ndim.- ndarray.size
общее количество элементов массива. Это равно произведению элементов
shape.- ndarray.dtype
объект, описывающий тип элементов в массиве. Можно создавать или указывать dtype с помощью стандартных типов Python. Дополнительно NumPy предоставляет свои собственные типы. numpy.int32, numpy.int16 и numpy.float64 — некоторые примеры.
- ndarray.itemsize
размер в байтах каждого элемента массива. Например, массив элементов типа
float64имеетitemsize8 (=64/8), в то время как один из типаcomplex32имеетitemsize4 (=32/8). Это эквивалентноndarray.dtype.itemsize.- ndarray.data
буфер, содержащий фактические элементы массива. Обычно нам не понадобится использовать этот атрибут, потому что мы будем обращаться к элементам массива с помощью средств индексации.
Пример#
>>> import numpy as np
>>> a = np.arange(15).reshape(3, 5)
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
>>> a.shape
(3, 5)
>>> a.ndim
2
>>> a.dtype.name
'int64'
>>> a.itemsize
8
>>> a.size
15
>>> type(a)
Создание массивов#
Существует несколько способов создания массивов.
Например, можно создать массив из обычного списка или кортежа Python
с помощью array функции. Тип результирующего массива выводится из типа элементов в последовательностях.
>>> import numpy as np
>>> a = np.array([2, 3, 4])
>>> a
array([2, 3, 4])
>>> a.dtype
dtype('int64')
>>> b = np.array([1.2, 3.5, 5.1])
>>> b.dtype
dtype('float64')
Частая ошибка заключается в вызове array с несколькими аргументами, а не предоставлением одной последовательности в качестве аргумента.
>>> a = np.array(1, 2, 3, 4) # WRONG
Traceback (most recent call last):
...
TypeError: array() takes from 1 to 2 positional arguments but 4 were given
>>> a = np.array([1, 2, 3, 4]) # RIGHT
array преобразует последовательности последовательностей в двумерные массивы, последовательности последовательностей последовательностей в трехмерные массивы и так далее.
>>> b = np.array([(1.5, 2, 3), (4, 5, 6)])
>>> b
array([[1.5, 2. , 3. ],
[4. , 5. , 6. ]])
Тип массива также может быть явно указан при создании:
>>> c = np.array([[1, 2], [3, 4]], dtype=complex)
>>> c
array([[1.+0.j, 2.+0.j],
[3.+0.j, 4.+0.j]])
Часто элементы массива изначально неизвестны, но его размер известен. Поэтому NumPy предлагает несколько функций для создания массивов с начальным заполнителем. Это минимизирует необходимость расширения массивов, что является дорогой операцией.
Функция zeros создаёт массив, заполненный нулями, функция
ones создает массив, заполненный единицами, а функция empty
создаёт массив, начальное содержимое которого случайно и зависит от состояния памяти. По умолчанию dtype созданного массива —
float64, но это можно указать через аргумент ключевого слова dtype.
>>> np.zeros((3, 4))
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
>>> np.ones((2, 3, 4), dtype=np.int16)
array([[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]],
[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]], dtype=int16)
>>> np.empty((2, 3))
array([[3.73603959e-262, 6.02658058e-154, 6.55490914e-260], # may vary
[5.30498948e-313, 3.14673309e-307, 1.00000000e+000]])
Для создания последовательностей чисел NumPy предоставляет arange функция
которая аналогична встроенной в Python range, но возвращает
массив.
>>> np.arange(10, 30, 5)
array([10, 15, 20, 25])
>>> np.arange(0, 2, 0.3) # it accepts float arguments
array([0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8])
Когда arange используется с аргументами с плавающей точкой, обычно невозможно предсказать количество полученных элементов из-за конечной точности чисел с плавающей точкой. По этой причине обычно лучше использовать функцию linspace который получает в качестве аргумента количество
элементов, которые мы хотим, вместо шага:
>>> from numpy import pi
>>> np.linspace(0, 2, 9) # 9 numbers from 0 to 2
array([0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.5 , 1.75, 2. ])
>>> x = np.linspace(0, 2 * pi, 100) # useful to evaluate function at lots of points
>>> f = np.sin(x)
Смотрите также
array,
zeros,
zeros_like,
ones,
ones_like,
empty,
empty_like,
arange,
linspace,
random.Generator.random,
random.Generator.normal,
fromfunction,
fromfile
Вывод массивов#
При выводе массива NumPy отображает его аналогично вложенным спискам, но со следующей структурой:
последняя ось выводится слева направо,
предпоследний печатается сверху вниз,
остальные также выводятся сверху вниз, с каждым срезом, отделённым от следующего пустой строкой.
Одномерные массивы выводятся как строки, двумерные как матрицы, а трёхмерные как списки матриц.
>>> a = np.arange(6) # 1d array
>>> print(a)
[0 1 2 3 4 5]
>>>
>>> b = np.arange(12).reshape(4, 3) # 2d array
>>> print(b)
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
>>>
>>> c = np.arange(24).reshape(2, 3, 4) # 3d array
>>> print(c)
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
См. ниже для получения дополнительных сведений о reshape.
Если массив слишком велик для печати, NumPy автоматически пропускает центральную часть массива и выводит только углы:
>>> print(np.arange(10000))
[ 0 1 2 ... 9997 9998 9999]
>>>
>>> print(np.arange(10000).reshape(100, 100))
[[ 0 1 2 ... 97 98 99]
[ 100 101 102 ... 197 198 199]
[ 200 201 202 ... 297 298 299]
...
[9700 9701 9702 ... 9797 9798 9799]
[9800 9801 9802 ... 9897 9898 9899]
[9900 9901 9902 ... 9997 9998 9999]]
Чтобы отключить это поведение и заставить NumPy выводить весь массив, вы можете изменить параметры вывода с помощью set_printoptions.
>>> np.set_printoptions(threshold=sys.maxsize) # sys module should be imported
Базовые операции#
Арифметические операторы применяются к массивам поэлементно. Создаётся новый массив и заполняется результатом.
>>> a = np.array([20, 30, 40, 50])
>>> b = np.arange(4)
>>> b
array([0, 1, 2, 3])
>>> c = a - b
>>> c
array([20, 29, 38, 47])
>>> b**2
array([0, 1, 4, 9])
>>> 10 * np.sin(a)
array([ 9.12945251, -9.88031624, 7.4511316 , -2.62374854])
>>> a < 35
array([ True, True, False, False])
В отличие от многих матричных языков, оператор произведения * работает поэлементно в массивах NumPy. Матричное произведение может быть выполнено с использованием @ оператор (в python >=3.5) или dot функция или метод:
>>> A = np.array([[1, 1],
... [0, 1]])
>>> B = np.array([[2, 0],
... [3, 4]])
>>> A * B # elementwise product
array([[2, 0],
[0, 4]])
>>> A @ B # matrix product
array([[5, 4],
[3, 4]])
>>> A.dot(B) # another matrix product
array([[5, 4],
[3, 4]])
Некоторые операции, такие как += и *=, действуют на месте, чтобы изменить
существующий массив, а не создать новый.
>>> rg = np.random.default_rng(1) # create instance of default random number generator
>>> a = np.ones((2, 3), dtype=int)
>>> b = rg.random((2, 3))
>>> a *= 3
>>> a
array([[3, 3, 3],
[3, 3, 3]])
>>> b += a
>>> b
array([[3.51182162, 3.9504637 , 3.14415961],
[3.94864945, 3.31183145, 3.42332645]])
>>> a += b # b is not automatically converted to integer type
Traceback (most recent call last):
...
numpy._core._exceptions._UFuncOutputCastingError: Cannot cast ufunc 'add' output from dtype('float64') to dtype('int64') with casting rule 'same_kind'
При работе с массивами разных типов тип результирующего массива соответствует более общему или точному (поведение, известное как повышение типа).
>>> a = np.ones(3, dtype=np.int32)
>>> b = np.linspace(0, pi, 3)
>>> b.dtype.name
'float64'
>>> c = a + b
>>> c
array([1. , 2.57079633, 4.14159265])
>>> c.dtype.name
'float64'
>>> d = np.exp(c * 1j)
>>> d
array([ 0.54030231+0.84147098j, -0.84147098+0.54030231j,
-0.54030231-0.84147098j])
>>> d.dtype.name
'complex128'
Многие унарные операции, такие как вычисление суммы всех элементов в
массиве, реализованы как методы ndarray класс.
>>> a = rg.random((2, 3))
>>> a
array([[0.82770259, 0.40919914, 0.54959369],
[0.02755911, 0.75351311, 0.53814331]])
>>> a.sum()
3.1057109529998157
>>> a.min()
0.027559113243068367
>>> a.max()
0.8277025938204418
По умолчанию эти операции применяются к массиву, как если бы это был список чисел, независимо от его формы. Однако, указав axis
параметр позволяет применять операцию вдоль указанной оси
массива:
>>> b = np.arange(12).reshape(3, 4)
>>> b
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> b.sum(axis=0) # sum of each column
array([12, 15, 18, 21])
>>>
>>> b.min(axis=1) # min of each row
array([0, 4, 8])
>>>
>>> b.cumsum(axis=1) # cumulative sum along each row
array([[ 0, 1, 3, 6],
[ 4, 9, 15, 22],
[ 8, 17, 27, 38]])
Универсальные функции#
NumPy предоставляет знакомые математические функции, такие как sin, cos и
exp. В NumPy они называются «универсальными
функциями» (ufunc). Внутри NumPy эти функции работают поэлементно над массивом, создавая массив на выходе.
>>> B = np.arange(3)
>>> B
array([0, 1, 2])
>>> np.exp(B)
array([1. , 2.71828183, 7.3890561 ])
>>> np.sqrt(B)
array([0. , 1. , 1.41421356])
>>> C = np.array([2., -1., 4.])
>>> np.add(B, C)
array([2., 0., 6.])
Смотрите также
all,
any,
apply_along_axis,
argmax,
argmin,
argsort,
average,
bincount,
ceil,
clip,
conj,
corrcoef,
cov,
cross,
cumprod,
cumsum,
diff,
dot,
floor,
inner,
invert,
lexsort,
max,
maximum,
mean,
median,
min,
minimum,
nonzero,
outer,
prod,
re,
round,
sort,
std,
sum,
trace,
transpose,
var,
vdot,
vectorize,
where
Индексирование, срезы и итерация#
Одномерный массивы могут индексироваться, срезаться и итерироваться, почти как списки и другие последовательности Python.
>>> a = np.arange(10)**3
>>> a
array([ 0, 1, 8, 27, 64, 125, 216, 343, 512, 729])
>>> a[2]
8
>>> a[2:5]
array([ 8, 27, 64])
>>> # equivalent to a[0:6:2] = 1000;
>>> # from start to position 6, exclusive, set every 2nd element to 1000
>>> a[:6:2] = 1000
>>> a
array([1000, 1, 1000, 27, 1000, 125, 216, 343, 512, 729])
>>> a[::-1] # reversed a
array([ 729, 512, 343, 216, 125, 1000, 27, 1000, 1, 1000])
>>> for i in a:
... print(i**(1 / 3.))
...
9.999999999999998 # may vary
1.0
9.999999999999998
3.0
9.999999999999998
4.999999999999999
5.999999999999999
6.999999999999999
7.999999999999999
8.999999999999998
Многомерный массивы могут иметь один индекс на ось. Эти индексы указываются в кортеже, разделённом запятыми:
>>> def f(x, y):
... return 10 * x + y
...
>>> b = np.fromfunction(f, (5, 4), dtype=int)
>>> b
array([[ 0, 1, 2, 3],
[10, 11, 12, 13],
[20, 21, 22, 23],
[30, 31, 32, 33],
[40, 41, 42, 43]])
>>> b[2, 3]
23
>>> b[0:5, 1] # each row in the second column of b
array([ 1, 11, 21, 31, 41])
>>> b[:, 1] # equivalent to the previous example
array([ 1, 11, 21, 31, 41])
>>> b[1:3, :] # each column in the second and third row of b
array([[10, 11, 12, 13],
[20, 21, 22, 23]])
. Из-за
изменения в реализации некоторые очень тонкие тесты могут не пройти, хотя раньше
проходили.:
>>> b[-1] # the last row. Equivalent to b[-1, :]
array([40, 41, 42, 43])
Выражение в квадратных скобках в b[i] рассматривается как i
за которым следует столько экземпляров : по мере необходимости для представления
оставшихся осей. NumPy также позволяет записывать это с использованием точек как
b[i, ...].
The точки (...) представляют столько двоеточий, сколько необходимо для создания
полного кортежа индексации. Например, если x является массивом с 5
осями, тогда
x[1, 2, ...]эквивалентноx[1, 2, :, :, :],x[..., 3]tox[:, :, :, :, 3]иx[4, ..., 5, :]tox[4, :, :, 5, :].
>>> c = np.array([[[ 0, 1, 2], # a 3D array (two stacked 2D arrays)
... [ 10, 12, 13]],
... [[100, 101, 102],
... [110, 112, 113]]])
>>> c.shape
(2, 2, 3)
>>> c[1, ...] # same as c[1, :, :] or c[1]
array([[100, 101, 102],
[110, 112, 113]])
>>> c[..., 2] # same as c[:, :, 2]
array([[ 2, 13],
[102, 113]])
Итерация по многомерным массивам выполняется относительно первой оси:
>>> for row in b:
... print(row)
...
[0 1 2 3]
[10 11 12 13]
[20 21 22 23]
[30 31 32 33]
[40 41 42 43]
Однако, если нужно выполнить операцию над каждым элементом в массиве, можно использовать flat атрибут, который является
итератор
по всем элементам массива:
>>> for element in b.flat:
... print(element)
...
0
1
2
3
10
11
12
13
20
21
22
23
30
31
32
33
40
41
42
43
Смотрите также
Индексирование в ndarrays,
Подпрограммы индексирования (ссылка),
newaxis,
ndenumerate,
indices
Манипуляция формой#
Изменение формы массива#
Массив имеет форму, заданную количеством элементов вдоль каждой оси:
>>> a = np.floor(10 * rg.random((3, 4)))
>>> a
array([[3., 7., 3., 4.],
[1., 4., 2., 2.],
[7., 2., 4., 9.]])
>>> a.shape
(3, 4)
Форма массива может быть изменена с помощью различных команд. Обратите внимание, что следующие три команды возвращают изменённый массив, но не изменяют исходный массив:
>>> a.ravel() # returns the array, flattened
array([3., 7., 3., 4., 1., 4., 2., 2., 7., 2., 4., 9.])
>>> a.reshape(6, 2) # returns the array with a modified shape
array([[3., 7.],
[3., 4.],
[1., 4.],
[2., 2.],
[7., 2.],
[4., 9.]])
>>> a.T # returns the array, transposed
array([[3., 1., 7.],
[7., 4., 2.],
[3., 2., 4.],
[4., 2., 9.]])
>>> a.T.shape
(4, 3)
>>> a.shape
(3, 4)
Порядок элементов в массиве, полученном из ravel обычно «в стиле C», то есть самый правый индекс «меняется быстрее всего», поэтому элемент после a[0, 0] является a[0, 1]. Если массив преобразуется к другой форме, он снова рассматривается как "C-стиль". NumPy обычно создаёт массивы, хранящиеся в этом порядке, поэтому ravel обычно не потребует
копирования своего аргумента, но если массив был создан путем взятия срезов другого
массива или создан с необычными опциями, может потребоваться его копирование. Функции ravel и reshape также можно указать, используя необязательный аргумент, использовать массивы в стиле FORTRAN, в которых самый левый индекс изменяется быстрее всего.
The reshape функция возвращает свой
аргумент с изменённой формой, тогда как
ndarray.resize метод изменяет сам массив:
>>> a
array([[3., 7., 3., 4.],
[1., 4., 2., 2.],
[7., 2., 4., 9.]])
>>> a.resize((2, 6))
>>> a
array([[3., 7., 3., 4., 1., 4.],
[2., 2., 7., 2., 4., 9.]])
Если размерность задана как -1 в операции изменения формы, другие размерности автоматически вычисляются:
>>> a.reshape(3, -1)
array([[3., 7., 3., 4.],
[1., 4., 2., 2.],
[7., 2., 4., 9.]])
Смотрите также
Объединение различных массивов#
Несколько массивов могут быть объединены вместе по разным осям:
>>> a = np.floor(10 * rg.random((2, 2)))
>>> a
array([[9., 7.],
[5., 2.]])
>>> b = np.floor(10 * rg.random((2, 2)))
>>> b
array([[1., 9.],
[5., 1.]])
>>> np.vstack((a, b))
array([[9., 7.],
[5., 2.],
[1., 9.],
[5., 1.]])
>>> np.hstack((a, b))
array([[9., 7., 1., 9.],
[5., 2., 5., 1.]])
Функция column_stack укладывает 1D-массивы как столбцы в 2D-массив.
Эквивалентно hstack только для 2D массивов:
>>> from numpy import newaxis
>>> np.column_stack((a, b)) # with 2D arrays
array([[9., 7., 1., 9.],
[5., 2., 5., 1.]])
>>> a = np.array([4., 2.])
>>> b = np.array([3., 8.])
>>> np.column_stack((a, b)) # returns a 2D array
array([[4., 3.],
[2., 8.]])
>>> np.hstack((a, b)) # the result is different
array([4., 2., 3., 8.])
>>> a[:, newaxis] # view `a` as a 2D column vector
array([[4.],
[2.]])
>>> np.column_stack((a[:, newaxis], b[:, newaxis]))
array([[4., 3.],
[2., 8.]])
>>> np.hstack((a[:, newaxis], b[:, newaxis])) # the result is the same
array([[4., 3.],
[2., 8.]])
В общем случае для массивов с более чем двумя измерениями,
hstack складывает вдоль их вторых
осей, vstack складывает вдоль их
первых осей, и concatenate
позволяет использовать необязательные аргументы, указывающие номер оси, вдоль
которой должна происходить конкатенация.
Примечание
В сложных случаях, r_ и c_ полезны для создания массивов путем укладки чисел вдоль одной оси. Они позволяют использовать литералы диапазонов :.
>>> np.r_[1:4, 0, 4]
array([1, 2, 3, 0, 4])
При использовании с массивами в качестве аргументов,
r_ и
c_ похожи на
vstack и
hstack в их поведении по умолчанию,
но допускают необязательный аргумент, указывающий номер оси, вдоль
которой выполняется конкатенация.
Смотрите также
hstack,
vstack,
column_stack,
concatenate,
c_,
r_
Разделение одного массива на несколько меньших#
Используя hsplitвы можете разделить массив вдоль его горизонтальной оси, либо указав количество возвращаемых массивов одинаковой формы, либо указав столбцы, после которых должно произойти разделение:
>>> a = np.floor(10 * rg.random((2, 12)))
>>> a
array([[6., 7., 6., 9., 0., 5., 4., 0., 6., 8., 5., 2.],
[8., 5., 5., 7., 1., 8., 6., 7., 1., 8., 1., 0.]])
>>> # Split `a` into 3
>>> np.hsplit(a, 3)
[array([[6., 7., 6., 9.],
[8., 5., 5., 7.]]), array([[0., 5., 4., 0.],
[1., 8., 6., 7.]]), array([[6., 8., 5., 2.],
[1., 8., 1., 0.]])]
>>> # Split `a` after the third and the fourth column
>>> np.hsplit(a, (3, 4))
[array([[6., 7., 6.],
[8., 5., 5.]]), array([[9.],
[7.]]), array([[0., 5., 4., 0., 6., 8., 5., 2.],
[1., 8., 6., 7., 1., 8., 1., 0.]])]
vsplit разделяет по вертикальной
оси, и array_split позволяет
указать, вдоль какой оси разделять.
Копии и представления#
При операциях и манипуляциях с массивами их данные иногда копируются в новый массив, а иногда нет. Это часто вызывает путаницу у новичков. Есть три случая:
Без копирования вообще#
Простые присваивания не создают копий объектов или их данных.
>>> a = np.array([[ 0, 1, 2, 3],
... [ 4, 5, 6, 7],
... [ 8, 9, 10, 11]])
>>> b = a # no new object is created
>>> b is a # a and b are two names for the same ndarray object
True
Python передаёт изменяемые объекты по ссылке, поэтому вызовы функций не создают копий.
>>> def f(x):
... print(id(x))
...
>>> id(a) # id is a unique identifier of an object
148293216 # may vary
>>> f(a)
148293216 # may vary
Представление или поверхностная копия#
Различные объекты массивов могут использовать одни и те же данные. view метод
создаёт новый объект массива, который ссылается на те же данные.
>>> c = a.view()
>>> c is a
False
>>> c.base is a # c is a view of the data owned by a
True
>>> c.flags.owndata
False
>>>
>>> c = c.reshape((2, 6)) # a's shape doesn't change, reassigned c is still a view of a
>>> a.shape
(3, 4)
>>> c[0, 4] = 1234 # a's data changes
>>> a
array([[ 0, 1, 2, 3],
[1234, 5, 6, 7],
[ 8, 9, 10, 11]])
Срез массива возвращает его представление:
>>> s = a[:, 1:3]
>>> s[:] = 10 # s[:] is a view of s. Note the difference between s = 10 and s[:] = 10
>>> a
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
Глубокая копия#
The copy метод создает полную копию массива и его данных.
>>> d = a.copy() # a new array object with new data is created
>>> d is a
False
>>> d.base is a # d doesn't share anything with a
False
>>> d[0, 0] = 9999
>>> a
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
Иногда copy следует вызывать после среза, если исходный массив больше не требуется.
Например, предположим a является огромным промежуточным результатом, а конечный результат b содержит только небольшую часть a, следует создать глубокую копию при конструировании b со срезом:
>>> a = np.arange(int(1e8))
>>> b = a[:100].copy()
>>> del a # the memory of ``a`` can be released.
Если b = a[:100] используется вместо, a ссылается на b и будет сохраняться в памяти, даже если del a выполняется.
Смотрите также Копии и представления.
Обзор функций и методов#
Вот список некоторых полезных функций и методов NumPy, упорядоченных по категориям. См. Процедуры и объекты по темам для полного списка.
- Создание массива
arange,array,copy,empty,empty_like,eye,fromfile,fromfunction,identity,linspace,logspace,mgrid,ogrid,ones,ones_like,r_,zeros,zeros_like- Преобразования
ndarray.astype,atleast_1d,atleast_2d,atleast_3d, mat- Манипуляции
array_split,column_stack,concatenate,diagonal,dsplit,dstack,hsplit,hstack,ndarray.item,newaxis,ravel,repeat,reshape,resize,squeeze,swapaxes,take,transpose,vsplit,vstack- Вопросы
- Упорядочивание
- Операции
choose,compress,cumprod,cumsum,inner,ndarray.fill,imag,prod,put,putmask,real,sum- Основная статистика
- Basic Linear Algebra
cross,dot,outer,linalg.svd,vdot
Менее базовый#
Правила трансляции#
Трансляция позволяет универсальным функциям осмысленно работать с входными данными, которые не имеют точно такой же формы.
Первое правило трансляции заключается в том, что если все входные массивы не имеют одинакового количества измерений, "1" будет неоднократно добавляться в начало форм меньших массивов до тех пор, пока все массивы не будут иметь одинаковое количество измерений.
Второе правило трансляции гарантирует, что массивы размером 1 вдоль определённого измерения действуют так, как если бы они имели размер массива с наибольшей формой вдоль этого измерения. Значение элемента массива предполагается одинаковым вдоль этого измерения для «транслируемого» массива.
После применения правил трансляции размеры всех массивов должны совпадать. Подробнее можно найти в Трансляция (Broadcasting).
Расширенная индексация и трюки с индексами#
NumPy предоставляет больше возможностей индексации, чем обычные последовательности Python. В дополнение к индексации целыми числами и срезами, как мы видели ранее, массивы могут индексироваться массивами целых чисел и массивами булевых значений.
Индексирование с массивами индексов#
>>> a = np.arange(12)**2 # the first 12 square numbers
>>> i = np.array([1, 1, 3, 8, 5]) # an array of indices
>>> a[i] # the elements of `a` at the positions `i`
array([ 1, 1, 9, 64, 25])
>>>
>>> j = np.array([[3, 4], [9, 7]]) # a bidimensional array of indices
>>> a[j] # the same shape as `j`
array([[ 9, 16],
[81, 49]])
Когда индексируемый массив a является многомерным, единый массив индексов ссылается на первое измерение a. Следующий пример демонстрирует это поведение, преобразуя изображение меток в цветное изображение с использованием палитры.
>>> palette = np.array([[0, 0, 0], # black
... [255, 0, 0], # red
... [0, 255, 0], # green
... [0, 0, 255], # blue
... [255, 255, 255]]) # white
>>> image = np.array([[0, 1, 2, 0], # each value corresponds to a color in the palette
... [0, 3, 4, 0]])
>>> palette[image] # the (2, 4, 3) color image
array([[[ 0, 0, 0],
[255, 0, 0],
[ 0, 255, 0],
[ 0, 0, 0]],
[[ 0, 0, 0],
[ 0, 0, 255],
[255, 255, 255],
[ 0, 0, 0]]])
Мы также можем дать индексы для более чем одного измерения. Массивы индексов для каждого измерения должны иметь одинаковую форму.
>>> a = np.arange(12).reshape(3, 4)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> i = np.array([[0, 1], # indices for the first dim of `a`
... [1, 2]])
>>> j = np.array([[2, 1], # indices for the second dim
... [3, 3]])
>>>
>>> a[i, j] # i and j must have equal shape
array([[ 2, 5],
[ 7, 11]])
>>>
>>> a[i, 2]
array([[ 2, 6],
[ 6, 10]])
>>>
>>> a[:, j]
array([[[ 2, 1],
[ 3, 3]],
[[ 6, 5],
[ 7, 7]],
[[10, 9],
[11, 11]]])
В Python, arr[i, j] точно такой же, как arr[(i, j)]—так что мы можем поместить i и j в tuple и затем выполнить индексацию с этим.
>>> l = (i, j)
>>> # equivalent to a[i, j]
>>> a[l]
array([[ 2, 5],
[ 7, 11]])
Однако мы не можем сделать это, поместив i и j в массив, потому что этот массив будет интерпретироваться как индексация первого измерения a.
>>> s = np.array([i, j])
>>> # not what we want
>>> a[s]
Traceback (most recent call last):
File "" , line 1, in Еще одно распространенное использование индексирования с массивами — поиск максимального значения временных рядов:
>>> time = np.linspace(20, 145, 5) # time scale
>>> data = np.sin(np.arange(20)).reshape(5, 4) # 4 time-dependent series
>>> time
array([ 20. , 51.25, 82.5 , 113.75, 145. ])
>>> data
array([[ 0. , 0.84147098, 0.90929743, 0.14112001],
[-0.7568025 , -0.95892427, -0.2794155 , 0.6569866 ],
[ 0.98935825, 0.41211849, -0.54402111, -0.99999021],
[-0.53657292, 0.42016704, 0.99060736, 0.65028784],
[-0.28790332, -0.96139749, -0.75098725, 0.14987721]])
>>> # index of the maxima for each series
>>> ind = data.argmax(axis=0)
>>> ind
array([2, 0, 3, 1])
>>> # times corresponding to the maxima
>>> time_max = time[ind]
>>>
>>> data_max = data[ind, range(data.shape[1])] # => data[ind[0], 0], data[ind[1], 1]...
>>> time_max
array([ 82.5 , 20. , 113.75, 51.25])
>>> data_max
array([0.98935825, 0.84147098, 0.99060736, 0.6569866 ])
>>> np.all(data_max == data.max(axis=0))
True
Вы также можете использовать индексацию с массивами в качестве цели для присваивания:
>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> a[[1, 3, 4]] = 0
>>> a
array([0, 0, 2, 0, 0])
Однако, когда список индексов содержит повторения, присваивание выполняется несколько раз, оставляя последнее значение:
>>> a = np.arange(5)
>>> a[[0, 0, 2]] = [1, 2, 3]
>>> a
array([2, 1, 3, 3, 4])
Это достаточно разумно, но будьте осторожны, если хотите использовать Python
+= конструкция, так как она может не делать то, что вы ожидаете:
>>> a = np.arange(5)
>>> a[[0, 0, 2]] += 1
>>> a
array([1, 1, 3, 3, 4])
Хотя 0 встречается дважды в списке индексов, 0-й элемент
увеличивается только один раз. Это потому, что Python требует a += 1 быть
эквивалентным a = a + 1.
Индексирование с булевыми массивами#
Когда мы индексируем массивы массивами (целочисленных) индексов, мы предоставляем список индексов для выбора. С булевыми индексами подход иной; мы явно выбираем, какие элементы в массиве нам нужны, а какие нет.
Наиболее естественный способ, который можно придумать для булевой индексации, — использовать булевы массивы, которые имеют та же форма как исходный массив:
>>> a = np.arange(12).reshape(3, 4)
>>> b = a > 4
>>> b # `b` is a boolean with `a`'s shape
array([[False, False, False, False],
[False, True, True, True],
[ True, True, True, True]])
>>> a[b] # 1d array with the selected elements
array([ 5, 6, 7, 8, 9, 10, 11])
Это свойство может быть очень полезным в присваиваниях:
>>> a[b] = 0 # All elements of `a` higher than 4 become 0
>>> a
array([[0, 1, 2, 3],
[4, 0, 0, 0],
[0, 0, 0, 0]])
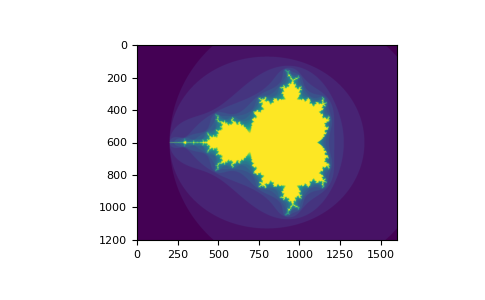
Вы можете посмотреть следующий пример, чтобы увидеть, как использовать булево индексирование для создания изображения Множество Мандельброта:
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> def mandelbrot(h, w, maxit=20, r=2):
... """Returns an image of the Mandelbrot fractal of size (h,w)."""
... x = np.linspace(-2.5, 1.5, 4*h+1)
... y = np.linspace(-1.5, 1.5, 3*w+1)
... A, B = np.meshgrid(x, y)
... C = A + B*1j
... z = np.zeros_like(C)
... divtime = maxit + np.zeros(z.shape, dtype=int)
...
... for i in range(maxit):
... z = z**2 + C
... diverge = abs(z) > r # who is diverging
... div_now = diverge & (divtime == maxit) # who is diverging now
... divtime[div_now] = i # note when
... z[diverge] = r # avoid diverging too much
...
... return divtime
>>> plt.clf()
>>> plt.imshow(mandelbrot(400, 400))
Второй способ индексации с булевыми значениями более похож на целочисленную индексацию; для каждого измерения массива мы даем одномерный булев массив, выбирающий нужные срезы:
>>> a = np.arange(12).reshape(3, 4)
>>> b1 = np.array([False, True, True]) # first dim selection
>>> b2 = np.array([True, False, True, False]) # second dim selection
>>>
>>> a[b1, :] # selecting rows
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> a[b1] # same thing
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> a[:, b2] # selecting columns
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])
>>>
>>> a[b1, b2] # a weird thing to do
array([ 4, 10])
Обратите внимание, что длина одномерного булева массива должна совпадать с
длиной измерения (или оси), которое вы хотите срезать. В предыдущем
примере, b1 имеет длину 3 (количество строки в a), и
b2 (длиной 4) подходит для индексации 2-й оси (столбцов)
a.
Функция ix_()#
The ix_ Функция может использоваться для объединения различных векторов, чтобы получить результат для каждого n-кортежа. Например, если вы хотите вычислить все a+b*c для всех троек, взятых из каждого из векторов a, b и c:
>>> a = np.array([2, 3, 4, 5])
>>> b = np.array([8, 5, 4])
>>> c = np.array([5, 4, 6, 8, 3])
>>> ax, bx, cx = np.ix_(a, b, c)
>>> ax
array([[[2]],
[[3]],
[[4]],
[[5]]])
>>> bx
array([[[8],
[5],
[4]]])
>>> cx
array([[[5, 4, 6, 8, 3]]])
>>> ax.shape, bx.shape, cx.shape
((4, 1, 1), (1, 3, 1), (1, 1, 5))
>>> result = ax + bx * cx
>>> result
array([[[42, 34, 50, 66, 26],
[27, 22, 32, 42, 17],
[22, 18, 26, 34, 14]],
[[43, 35, 51, 67, 27],
[28, 23, 33, 43, 18],
[23, 19, 27, 35, 15]],
[[44, 36, 52, 68, 28],
[29, 24, 34, 44, 19],
[24, 20, 28, 36, 16]],
[[45, 37, 53, 69, 29],
[30, 25, 35, 45, 20],
[25, 21, 29, 37, 17]]])
>>> result[3, 2, 4]
17
>>> a[3] + b[2] * c[4]
17
Вы также можете реализовать reduce следующим образом:
>>> def ufunc_reduce(ufct, *vectors):
... vs = np.ix_(*vectors)
... r = ufct.identity
... for v in vs:
... r = ufct(r, v)
... return r
и затем использовать как:
>>> ufunc_reduce(np.add, a, b, c)
array([[[15, 14, 16, 18, 13],
[12, 11, 13, 15, 10],
[11, 10, 12, 14, 9]],
[[16, 15, 17, 19, 14],
[13, 12, 14, 16, 11],
[12, 11, 13, 15, 10]],
[[17, 16, 18, 20, 15],
[14, 13, 15, 17, 12],
[13, 12, 14, 16, 11]],
[[18, 17, 19, 21, 16],
[15, 14, 16, 18, 13],
[14, 13, 15, 17, 12]]])
Преимущество этой версии reduce по сравнению с обычным ufunc.reduce в том, что она использует правила трансляции чтобы избежать создания массива аргументов размером с выходной массив, умноженный на количество векторов.
Индексирование строками#
Приемы и советы#
Здесь мы приводим список коротких и полезных советов.
«Автоматическое» изменение формы#
Чтобы изменить размеры массива, вы можете опустить один из размеров, который затем будет определён автоматически:
>>> a = np.arange(30)
>>> b = a.reshape((2, -1, 3)) # -1 means "whatever is needed"
>>> b.shape
(2, 5, 3)
>>> b
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]],
[[15, 16, 17],
[18, 19, 20],
[21, 22, 23],
[24, 25, 26],
[27, 28, 29]]])
Векторное объединение#
Как построить двумерный массив из списка векторов-строк одинакового размера?
В MATLAB это довольно просто: если x и y являются двумя векторами одинаковой длины, вам нужно только сделать m=[x;y]. В NumPy это работает через функции column_stack, dstack, hstack и vstack,
в зависимости от измерения, в котором выполняется объединение. Например:
>>> x = np.arange(0, 10, 2)
>>> y = np.arange(5)
>>> m = np.vstack([x, y])
>>> m
array([[0, 2, 4, 6, 8],
[0, 1, 2, 3, 4]])
>>> xy = np.hstack([x, y])
>>> xy
array([0, 2, 4, 6, 8, 0, 1, 2, 3, 4])
Логика этих функций в более чем двух измерениях может быть странной.
Смотрите также
Гистограммы#
NumPy histogram функция, примененная к массиву, возвращает пару векторов: гистограмму массива и вектор границ бинов. Внимание:
matplotlib также имеет функцию построения гистограмм (называемую hist, как в Matlab), который отличается от такового в NumPy. Основное различие заключается в том, что pylab.hist автоматически строит гистограмму, в то время как
numpy.histogram только генерирует данные.
>>> import numpy as np
>>> rg = np.random.default_rng(1)
>>> import matplotlib.pyplot as plt
>>> # Build a vector of 10000 normal deviates with variance 0.5^2 and mean 2
>>> mu, sigma = 2, 0.5
>>> v = rg.normal(mu, sigma, 10000)
>>> # Plot a normalized histogram with 50 bins
>>> plt.hist(v, bins=50, density=True) # matplotlib version (plot)
(array...)
>>> # Compute the histogram with numpy and then plot it
>>> (n, bins) = np.histogram(v, bins=50, density=True) # NumPy version (no plot)
>>> plt.plot(.5 * (bins[1:] + bins[:-1]), n)
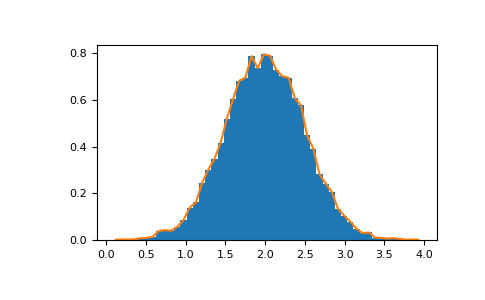
С Matplotlib >=3.4 вы также можете использовать plt.stairs(n, bins).