scipy.differentiate.

производная

scipy.differentiate.производная(f, x, *, args=(), допуски=None, maxiter=10, порядок=8, initial_step=0.5, step_factor=2.0, step_direction=0, preserve_shape=False, callback=None)

Вычислить производную поэлементной вещественной скалярной функции численно.

Для каждого элемента вывода f, derivative аппроксимирует первую производную от f в соответствующем элементе x используя дифференцирование методом конечных разностей.

Эта функция работает поэлементно, когда x, step_direction, и args содержат (транслируемые) массивы.

Параметры:

fcallable

Функция, производная которой требуется. Сигнатура должна быть:

f(xi: ndarray, *argsi) -> ndarray

где каждый элемент xi является конечным вещественным числом и argsi является кортежем, который может содержать произвольное количество массивов, совместимых по размерности с xi. f должна быть поэлементной функцией: каждый скалярный элемент f(xi)[j] должно равняться f(xi[j]) для допустимых индексов j. Он не должен изменять массив xi или массивы в argsi.

xfloat array_like

Абсциссы, в которых вычисляется производная. Должны быть совместимы с args и step_direction.

argsкортеж из array_like, необязательно

Дополнительные позиционные аргументы в виде массивов для передачи в f. Массивы должны быть совместимы для трансляции друг с другом и массивами init. Если вызываемый объект, для которого требуется найти корень, требует аргументов, которые не транслируются с x, оберните этот вызываемый объект с f такой, что f принимает только x и поддерживающие вещание *args.

допускисловарь чисел с плавающей точкой, опционально

Абсолютная и относительная погрешности. Допустимые ключи словаря:

• atol - абсолютный допуск на производную

• rtol - относительный допуск на производную

Итерация остановится, когда res.error < atol + rtol * abs(res.df). По умолчанию atol является наименьшим нормальным числом соответствующего типа данных, и по умолчанию rtol является квадратным корнем точности соответствующего типа данных.

порядокint, по умолчанию: 8

(Положительный целый) порядок формулы конечных разностей, которая будет использоваться. Нечетные целые числа будут округлены до следующего четного целого числа.

initial_stepfloat array_like, по умолчанию: 0.5

(Абсолютный) начальный размер шага для аппроксимации производной конечными разностями.

step_factorfloat, по умолчанию: 2.0

Коэффициент, на который умножается размер шага уменьшенный на каждой итерации; т.е. размер шага на итерации 1 равен initial_step/step_factor. Если step_factor < 1, последующие шаги будут больше начального шага; это может быть полезно, если шаги меньше некоторого порога нежелательны (например, из-за ошибки вычитательной отмены).

maxiterint, по умолчанию: 10

Максимальное количество итераций алгоритма для выполнения. См. Примечания.

step_directionцелочисленный array_like

Массив, представляющий направление шагов конечных разностей (для использования, когда x находится близко к границе области определения функции.) Должно быть совместимо с x и все args. Где 0 (по умолчанию), используются центральные разности; где отрицательное (например, -1), шаги неположительные; и где положительное (например, 1), все шаги неотрицательные.

preserve_shapebool, по умолчанию: False

В следующем, "аргументы f” относится к массиву xi и любые массивы внутри argsi. Пусть shape будет трансляционной формой x и все элементы args (что концептуально отличается от xi` and ``argsi передано в f).

• Когда preserve_shape=False (по умолчанию), f должен принимать аргументы любой совместимые формы для вещания.

• Когда preserve_shape=True, f должен принимать аргументы формы shape или shape + (n,), где (n,) это количество абсцисс, в которых вычисляется функция.

В любом случае, для каждого скалярного элемента xi[j] внутри xi, массив, возвращаемый f должен включать скаляр f(xi[j]) по тому же индексу. Следовательно, форма вывода всегда совпадает с формой ввода xi.

См. примеры.

callbackвызываемый объект, необязательный

Необязательная пользовательская функция, вызываемая перед первой итерацией и после каждой итерации. Вызывается как callback(res), где res является _RichResult аналогично тому, что возвращается derivative (но содержащий текущие значения всех переменных на данной итерации). Если callback вызывает StopIteration, алгоритм немедленно завершится и derivative вернёт результат. callback не должен изменять res или его атрибуты.

Возвращает:

res_RichResult

Объект, похожий на экземпляр scipy.optimize.OptimizeResult со следующими атрибутами. Описания написаны так, как будто значения будут скалярами; однако, если f возвращает массив, выходные данные будут массивами той же формы.

successлогический массив

True где алгоритм успешно завершился (статус 0); False в противном случае.

statusцелочисленный массив

Целое число, представляющее статус завершения алгоритма.

• 0 : Алгоритм сошелся к заданным допускам.

• -1 : Оценка ошибки увеличилась, поэтому итерация была прекращена.

• -2 : Достигнуто максимальное количество итераций.

• -3 : Встречено неконечное значение.

• -4 : Итерация была завершена callback.

• 1 : Алгоритм работает нормально (в callback только).

dfмассив float

Производная от f в x, если алгоритм завершился успешно.

ошибкамассив float

Оценка ошибки: величина разницы между текущей оценкой производной и оценкой в предыдущей итерации.

nitцелочисленный массив

Количество выполненных итераций алгоритма.

nfevцелочисленный массив

Количество точек, в которых f было вычислено.

xмассив float

Значение, при котором производная f была оценена (после трансляции с args и step_direction).

Смотрите также

jacobian, hessian

Примечания

Реализация была вдохновлена jacobi [1], numdifftools [2], и DERIVEST [3], но реализация следует теории рядов Тейлора более прямолинейно (и, возможно, наивно). На первой итерации производная оценивается с использованием формулы конечных разностей порядка порядок с максимальным размером шага initial_step. На каждой последующей итерации максимальный размер шага уменьшается на step_factor, и производная оценивается снова до достижения условия завершения. Оценка ошибки - это величина разницы между текущим приближением производной и приближением предыдущей итерации.

Шаблоны формул конечных разностей разработаны так, что абсциссы «вложены»: после f вычисляется в order + 1 точки в первой итерации, f вычисляется только в двух новых точках в каждой последующей итерации; order - 1 ранее вычисленные значения функции, требуемые формулой конечных разностей, повторно используются, и два значения функции (вычисления в точках, наиболее удалённых от x) не используются.

Шаги абсолютны. Когда размер шага мал относительно величины x, точность теряется; например, если x является 1e20, размер начального шага по умолчанию 0.5 не может быть разрешена. Соответственно, рассмотрите использование больших начальных размеров шага для больших величин x.

Стандартные допуски сложно удовлетворить в точках, где истинная производная равна нулю. Если производная может быть точно нулевой, рассмотрите указание абсолютного допуска (например, atol=1e-12) для улучшения сходимости.

Ссылки

[1]

Ханс Дембински (@HDembinski). jacobi. HDembinski/jacobi

[2]

Per A. Brodtkorb и John D’Errico. numdifftools. https://numdifftools.readthedocs.io/en/latest/

[3]

Джон Д’Эррико. DERIVEST: Адаптивная робастная численная дифференциация. https://www.mathworks.com/matlabcentral/fileexchange/13490-adaptive-robust-numerical-differentiation

[4]

Численное дифференцирование. Википедия. https://en.wikipedia.org/wiki/Numerical_differentiation

Примеры

Попробуйте в вашем браузере!

Вычислить производную np.exp в нескольких точках x.

>>> import numpy as np
>>> from scipy.differentiate import derivative
>>> f = np.exp
>>> df = np.exp  # true derivative
>>> x = np.linspace(1, 2, 5)
>>> res = derivative(f, x)
>>> res.df  # approximation of the derivative
array([2.71828183, 3.49034296, 4.48168907, 5.75460268, 7.3890561 ])
>>> res.error  # estimate of the error
array([7.13740178e-12, 9.16600129e-12, 1.17594823e-11, 1.51061386e-11,
       1.94262384e-11])
>>> abs(res.df - df(x))  # true error
array([2.53130850e-14, 3.55271368e-14, 5.77315973e-14, 5.59552404e-14,
       6.92779167e-14])

Показать сходимость аппроксимации при уменьшении шага. На каждой итерации шаг уменьшается на step_factor, поэтому для достаточно малого начального шага каждая итерация уменьшает ошибку на коэффициент 1/step_factor**order пока конечная точность арифметики не препятствует дальнейшему улучшению.

>>> import matplotlib.pyplot as plt
>>> iter = list(range(1, 12))  # maximum iterations
>>> hfac = 2  # step size reduction per iteration
>>> hdir = [-1, 0, 1]  # compare left-, central-, and right- steps
>>> order = 4  # order of differentiation formula
>>> x = 1
>>> ref = df(x)
>>> errors = []  # true error
>>> for i in iter:
...     res = derivative(f, x, maxiter=i, step_factor=hfac,
...                      step_direction=hdir, order=order,
...                      # prevent early termination
...                      tolerances=dict(atol=0, rtol=0))
...     errors.append(abs(res.df - ref))
>>> errors = np.array(errors)
>>> plt.semilogy(iter, errors[:, 0], label='left differences')
>>> plt.semilogy(iter, errors[:, 1], label='central differences')
>>> plt.semilogy(iter, errors[:, 2], label='right differences')
>>> plt.xlabel('iteration')
>>> plt.ylabel('error')
>>> plt.legend()
>>> plt.show()

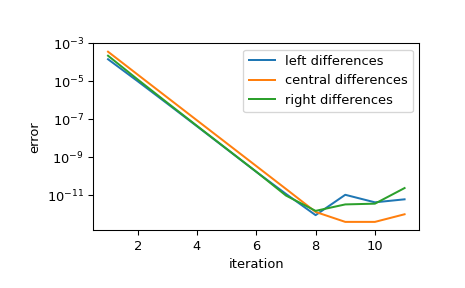
>>> (errors[1, 1] / errors[0, 1], 1 / hfac**order)
(0.06215223140159822, 0.0625)

Реализация векторизована по x, step_direction, и args. Функция вычисляется один раз перед первой итерацией для проверки входных данных и стандартизации, и один раз за итерацию после этого.

>>> def f(x, p):
...     f.nit += 1
...     return x**p
>>> f.nit = 0
>>> def df(x, p):
...     return p*x**(p-1)
>>> x = np.arange(1, 5)
>>> p = np.arange(1, 6).reshape((-1, 1))
>>> hdir = np.arange(-1, 2).reshape((-1, 1, 1))
>>> res = derivative(f, x, args=(p,), step_direction=hdir, maxiter=1)
>>> np.allclose(res.df, df(x, p))
True
>>> res.df.shape
(3, 5, 4)
>>> f.nit
2

По умолчанию, preserve_shape равно False, и поэтому вызываемый объект f может вызываться с массивами любых совместимых форм. Например:

>>> shapes = []
>>> def f(x, c):
...    shape = np.broadcast_shapes(x.shape, c.shape)
...    shapes.append(shape)
...    return np.sin(c*x)
>>>
>>> c = [1, 5, 10, 20]
>>> res = derivative(f, 0, args=(c,))
>>> shapes
[(4,), (4, 8), (4, 2), (3, 2), (2, 2), (1, 2)]

Чтобы понять, откуда берутся эти формы - и лучше понять, как derivative вычисляет точные результаты - обратите внимание, что более высокие значения c соответствуют синусоидам более высокой частоты. Синусоиды более высокой частоты заставляют производную функции изменяться быстрее, поэтому требуется больше вычислений функции для достижения целевой точности:

>>> res.nfev
array([11, 13, 15, 17], dtype=int32)

Начальный shape, (4,), соответствует вычислению функции в одной абсциссе и всех четырёх частотах; это используется для проверки входных данных и определения размера и типа массивов, которые хранят результаты. Следующая форма соответствует вычислению функции на начальной сетке абсцисс и всех четырёх частотах. Последующие вызовы функции вычисляют функцию ещё на двух абсциссах, увеличивая эффективный порядок аппроксимации на два. Однако в последующих вычислениях функции она вычисляется на меньшем количестве частот, потому что соответствующая производная уже сошлась к требуемой точности. Это экономит вычисления функции для улучшения производительности, но требует, чтобы функция принимала аргументы любой формы.

«Векторно-значные» функции вряд ли удовлетворяют этому требованию. Например, рассмотрим

>>> def f(x):
...    return [x, np.sin(3*x), x+np.sin(10*x), np.sin(20*x)*(x-1)**2]

Этот подынтегральный выражение несовместим с derivative как написано; например, форма вывода не будет такой же, как форма x. Такая функция мог может быть преобразовано в совместимую форму с введением дополнительных параметров, но это было бы неудобно. В таких случаях более простое решение — использовать preserve_shape.

>>> shapes = []
>>> def f(x):
...     shapes.append(x.shape)
...     x0, x1, x2, x3 = x
...     return [x0, np.sin(3*x1), x2+np.sin(10*x2), np.sin(20*x3)*(x3-1)**2]
>>>
>>> x = np.zeros(4)
>>> res = derivative(f, x, preserve_shape=True)
>>> shapes
[(4,), (4, 8), (4, 2), (4, 2), (4, 2), (4, 2)]

Здесь форма x является (4,). С preserve_shape=True, функция может быть вызвана с аргументом x формы (4,) или (4, n), и это то, что мы наблюдаем.

НазадОткрыть во вкладке