scipy.integrate.

quad_vec

scipy.integrate.quad_vec(f, a, b, epsabs=1e-200, epsrel=1e-08, norm='2', cache_size=100000000.0, limit=10000, workers=1, точки=None, квадратура=None, full_output=False, *, args=())

Адаптивное интегрирование векторнозначной функции.

Параметры:

fcallable

Векторнозначная функция f(x) для интегрирования.

afloat

Начальная точка.

bfloat

Конечная точка.

epsabsfloat, опционально

Абсолютная погрешность.

epsrelfloat, опционально

Относительный допуск.

norm{‘max’, ‘2’}, необязательно

Векторная норма для оценки ошибки.

cache_sizeint, необязательный

Количество байтов для использования в мемоизации.

limitfloat или int, опционально

Верхняя граница количества подынтервалов, используемых в адаптивном алгоритме.

workersint или вызываемый объект, подобный отображению, необязательный

Если workers является целым числом, часть вычислений выполняется параллельно, разделяясь на это количество задач (с использованием multiprocessing.pool.Pool). Укажите -1 использовать все доступные ядра процессора. В качестве альтернативы, предоставьте вызываемый объект, подобный map, такой как multiprocessing.pool.Pool.map для параллельной оценки популяции. Эта оценка выполняется как workers(func, iterable).

точкисписок, необязательный

Список дополнительных точек останова.

квадратура{‘gk21’, ‘gk15’, ‘trapezoid’}, опционально

Правило квадратуры для использования на подынтервалах. Опции: ‘gk21’ (правило Гаусса-Кронрода 21 точки), ‘gk15’ (правило Гаусса-Кронрода 15 точек), ‘trapezoid’ (составное правило трапеций). По умолчанию: ‘gk21’ для конечных интервалов и ‘gk15’ для (полу-)бесконечных.

full_outputbool, необязательно

Вернуть дополнительный info объект.

argsкортеж, необязательный

Дополнительные аргументы для передачи функции, если есть.

Добавлено в версии 1.8.0.

Возвращает:

res{float, array-like}

Оценка для результата

errfloat

Оценка ошибки для результата в заданной норме

infoobject

Возвращается только когда full_output=True. Объект результата с атрибутами:

successbool

Достигнута ли целевая точность интегрирования.

statusint

Индикатор сходимости: успех (0), неудача (1) и неудача из-за ошибки округления (2).

nevalint

Количество вычислений функции.

интервалыndarray, форма (num_intervals, 2)

Начальные и конечные точки интервалов разбиения.

интегралыndarray, форма (num_intervals, …)

Интеграл для каждого интервала. Обратите внимание, что максимум cache_size значения записываются, и массив может содержать nan для отсутствующих элементов.

ошибкиndarray, форма (num_intervals,)

Оцененная ошибка интегрирования для каждого интервала.

Примечания

Алгоритм в основном следует реализации алгоритмов DQAG* из QUADPACK, реализуя глобальный контроль ошибок и адаптивное разбиение.

Алгоритм здесь имеет некоторые отличия от подхода QUADPACK:

Вместо разделения одного интервала за раз, алгоритм разделяет N интервалов с наибольшими ошибками одновременно. Это позволяет (частично) распараллелить интегрирование.

Логика подразделения «следующих наибольших» интервалов сначала тогда не реализована, и мы полагаемся на указанное выше расширение, чтобы избежать концентрации только на «маленьких» интервалах.

Экстраполяция таблицы эпсилон Винна не используется (QUADPACK использует её для бесконечных интервалов). Это связано с тем, что алгоритм здесь предполагается работающим с векторнозначными функциями, в пользовательской норме, и расширение алгоритма эпсилон на этот случай не представляется общепринятым. Для max-нормы использование поэлементного эпсилона Винна могло бы быть возможным, но мы не делаем этого здесь, надеясь, что экстраполяция эпсилон в основном полезна в особых случаях.

Ссылки

[1] R. Piessens, E. de Doncker, QUADPACK (1983).

Примеры

Попробуйте в вашем браузере!

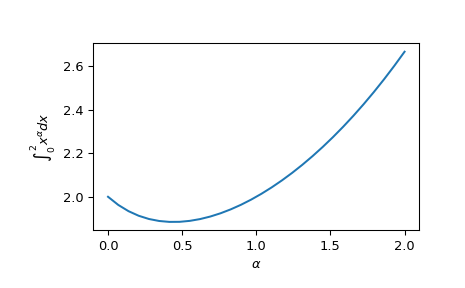
Мы можем вычислить интегралы векторнозначной функции:

>>> from scipy.integrate import quad_vec
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> alpha = np.linspace(0.0, 2.0, num=30)
>>> f = lambda x: x**alpha
>>> x0, x1 = 0, 2
>>> y, err = quad_vec(f, x0, x1)
>>> plt.plot(alpha, y)
>>> plt.xlabel(r"$\alpha$")
>>> plt.ylabel(r"$\int_{0}^{2} x^\alpha dx$")
>>> plt.show()

При использовании аргумента workers, следует убедиться, что основной модуль безопасен для импорта, например, переписав приведённый выше пример как:

from scipy.integrate import quad_vec
import numpy as np
import matplotlib.pyplot as plt

alpha = np.linspace(0.0, 2.0, num=30)
x0, x1 = 0, 2
def f(x):
    return x**alpha

if __name__ == "__main__":
    y, err = quad_vec(f, x0, x1, workers=2)

НазадОткрыть во вкладке