scipy.integrate.

solve_bvp#

scipy.integrate.solve_bvp(fun, bc, x, y, p=None, S=None, fun_jac=None, bc_jac=None, tol=0.001, max_nodes=1000, verbose=0, bc_tol=None)[источник]#

Решить краевую задачу для системы ОДУ.

Эта функция численно решает систему ОДУ первого порядка с двухточечными граничными условиями:

dy / dx = f(x, y, p) + S * y / (x - a), a <= x <= b
bc(y(a), y(b), p) = 0

Здесь x — одномерная независимая переменная, y(x) — n-мерная векторная функция, а p — k-мерный вектор неизвестных параметров, которые нужно найти вместе с y(x). Для определённости задачи должно быть n + k граничных условий, т.е. bc должна быть (n + k)-мерной функцией.

Последний сингулярный член в правой части системы является необязательным. Он определяется матрицей S размером n на n, так что решение должно удовлетворять S y(a) = 0. Это условие будет принудительно применяться во время итераций, поэтому оно не должно противоречить граничным условиям. См. [2] для объяснения, как этот член обрабатывается при численном решении краевых задач.

Задачи в комплексной области также могут быть решены. В этом случае y и p считаются комплексными, а f и bc предполагаются комплекснозначными функциями, но x остается вещественным. Заметим, что f и bc должны быть комплексно дифференцируемыми (удовлетворять уравнениям Коши-Римана [4]), иначе вам следует переформулировать вашу задачу для вещественных и мнимых частей отдельно. Чтобы решить задачу в комплексной области, передайте начальное приближение для y с комплексным типом данных (см. ниже).

Параметры:

funcallable

Правая часть системы. Сигнатура вызова: fun(x, y), или fun(x, y, p) если параметры присутствуют. Все аргументы являются ndarray: x с формой (m,), y с формой (n, m), означающей, что y[:, i] соответствует x[i], и p с формой (k,). Возвращаемое значение должно быть массивом с формой (n, m) и с той же структурой, что и y.

bccallable

Функция, оценивающая невязки граничных условий. Сигнатура вызова bc(ya, yb), или bc(ya, yb, p) если параметры присутствуют. Все аргументы являются ndarray: ya и yb с формой (n,), и p с формой (k,). Возвращаемое значение должно быть массивом с формой (n + k,).

xarray_like, shape (m,)

Начальная сетка. Должна быть строго возрастающей последовательностью вещественных чисел с x[0]=a и x[-1]=b.

yarray_like, форма (n, m)

Начальное предположение для значений функции в узлах сетки, i-й столбец соответствует x[i]. Для задач в комплексной области передайте y со сложным типом данных (даже если начальное приближение чисто вещественное).

parray_like с формой (k,) или None, опционально

Начальное предположение для неизвестных параметров. Если None (по умолчанию), предполагается, что задача не зависит от каких-либо параметров.

Sarray_like с формой (n, n) или None

Матрица, определяющая сингулярный член. Если None (по умолчанию), задача решается без сингулярного члена.

fun_jacвызываемый объект или None, опционально

Функция, вычисляющая производные f по y и p. Сигнатура вызова: fun_jac(x, y), или fun_jac(x, y, p) если присутствуют параметры. Возвращаемое значение должно содержать 1 или 2 элемента в следующем порядке:

df_dy : array_like формы (n, n, m), где элемент (i, j, q) равен d f_i(x_q, y_q, p) / d (y_q)_j.

df_dp : array_like с формой (n, k, m), где элемент (i, j, q) равен d f_i(x_q, y_q, p) / d p_j.

Здесь q нумерует узлы, в которых определены x и y, тогда как i и j нумеруют компоненты вектора. Если задача решена без неизвестных параметров, df_dp не должен возвращаться.

Если fun_jac равно None (по умолчанию), производные будут оценены с помощью прямых конечных разностей.

bc_jacвызываемый объект или None, опционально

Функция вычисления производных bc по ya, yb и p. Сигнатура вызова bc_jac(ya, yb), или bc_jac(ya, yb, p) если параметры присутствуют. Возвращаемое значение должно содержать 2 или 3 элемента в следующем порядке:

dbc_dya : array_like формы (n, n), где элемент (i, j) равен d bc_i(ya, yb, p) / d ya_j.

dbc_dyb : array_like с формой (n, n), где элемент (i, j) равен d bc_i(ya, yb, p) / d yb_j.

dbc_dp : array_like с формой (n, k), где элемент (i, j) равен d bc_i(ya, yb, p) / d p_j.

Если задача решена без неизвестных параметров, dbc_dp не должен быть возвращен.

Если bc_jac равно None (по умолчанию), производные будут оценены с помощью прямых конечных разностей.

tolfloat, опционально

Желаемая точность решения. Если мы определим r = y' - f(x, y), где y — найденное решение, тогда решатель пытается достичь на каждом интервале сетки norm(r / (1 + abs(f)) < tol, где norm оценивается в среднеквадратичном смысле (с использованием численной квадратурной формулы). По умолчанию 1e-3.

max_nodesint, необязательный

Максимально допустимое количество узлов сетки. При превышении алгоритм завершается. По умолчанию 1000.

verbose{0, 1, 2}, опционально

Уровень детализации алгоритма:

0 (по умолчанию) : работать без вывода сообщений.

1 : отобразить отчет о завершении.

2 : отображать прогресс во время итераций.

bc_tolfloat, опционально

Желаемая абсолютная погрешность для остатков граничных условий: bc значение должно удовлетворять abs(bc) < bc_tol покомпонентно. Равно tol по умолчанию. Допускается до 10 итераций для достижения этой точности.

Возвращает:

Объект Bunch со следующими определёнными полями:

solPPoly

Найдено решение для y как scipy.interpolate.PPoly например, кубический сплайн непрерывный C1.

pndarray или None, форма (k,)

Найденные параметры. None, если параметры отсутствовали в задаче.

xndarray, форма (m,)

Узлы конечной сетки.

yndarray, shape (n, m)

Значения решения в узлах сетки.

ypndarray, shape (n, m)

Производные решения в узлах сетки.

rms_residualsndarray, форма (m - 1,)

СКЗ относительных невязок на каждом интервале сетки (см. описание tol параметр).

niterint

Количество завершённых итераций.

statusint

Причина завершения алгоритма:

0: Алгоритм сошёлся к желаемой точности.

1: Превышено максимальное количество узлов сетки.

2: Обнаружена сингулярная матрица Якоби при решении системы коллокации.

messagestring

Словесное описание причины завершения.

successbool

True, если алгоритм сошелся к желаемой точности (status=0).

Примечания

Эта функция реализует алгоритм коллокации 4-го порядка с контролем невязок, аналогичный [1]. Система коллокации решается методом затухающего Ньютона с аффинно-инвариантной критериальной функцией, как описано в [3].

Обратите внимание, что в [1] Интегральные остатки определяются без нормализации по длинам интервалов. Таким образом, их определение отличается на множитель h**0.5 (h - длина интервала) от определения, используемого здесь.

Добавлено в версии 0.18.0.

Ссылки

[1] (1,2)

J. Kierzenka, L. F. Shampine, “A BVP Solver Based on Residual Control and the Maltab PSE”, ACM Trans. Math. Softw., Vol. 27, Number 3, pp. 299-316, 2001.

[2]

L.F. Shampine, P. H. Muir и H. Xu, «A User-Friendly Fortran BVP Solver», J. Numer. Anal., Ind. Appl. Math. (JNAIAM), Vol. 1, Number 2, pp. 201-217, 2006.

[3]

U. Ascher, R. Mattheij и R. Russell «Численное решение краевых задач для обыкновенных дифференциальных уравнений», Филадельфия, Пенсильвания: Общество промышленной и прикладной математики, 1995. DOI:10.1137/1.9781611971231

[4]

уравнения Коши-Римана на Википедии.

Примеры

В первом примере мы решаем задачу Брату:

y'' + k * exp(y) = 0
y(0) = y(1) = 0

для k = 1.

Мы переписываем уравнение как систему первого порядка и реализуем вычисление её правой части:

y1' = y2
y2' = -exp(y1)

>>> import numpy as np
>>> def fun(x, y):
...     return np.vstack((y[1], -np.exp(y[0])))

Реализовать оценку остатков граничных условий:

>>> def bc(ya, yb):
...     return np.array([ya[0], yb[0]])

Определите начальную сетку с 5 узлами:

>>> x = np.linspace(0, 1, 5)

Известно, что эта задача имеет два решения. Чтобы получить оба, мы используем два разных начальных приближения для y. Обозначим их индексами a и b.

>>> y_a = np.zeros((2, x.size))
>>> y_b = np.zeros((2, x.size))
>>> y_b[0] = 3

Теперь мы готовы запустить решатель.

>>> from scipy.integrate import solve_bvp
>>> res_a = solve_bvp(fun, bc, x, y_a)
>>> res_b = solve_bvp(fun, bc, x, y_b)

Построим график двух найденных решений. Мы воспользуемся тем, что решение представлено в виде сплайна, чтобы получить гладкий график.

>>> x_plot = np.linspace(0, 1, 100)
>>> y_plot_a = res_a.sol(x_plot)[0]
>>> y_plot_b = res_b.sol(x_plot)[0]
>>> import matplotlib.pyplot as plt
>>> plt.plot(x_plot, y_plot_a, label='y_a')
>>> plt.plot(x_plot, y_plot_b, label='y_b')
>>> plt.legend()
>>> plt.xlabel("x")
>>> plt.ylabel("y")
>>> plt.show()

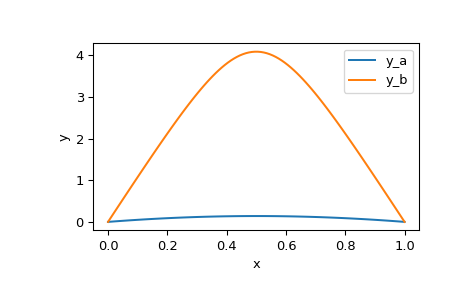
../../_images/scipy-integrate-solve_bvp-1_00_00.png

Мы видим, что два решения имеют схожую форму, но значительно различаются по масштабу.

Во втором примере мы решаем простую задачу Штурма-Лиувилля:

y'' + k**2 * y = 0
y(0) = y(1) = 0

Известно, что нетривиальное решение y = A * sin(k * x) возможно для k = pi * n, где n — целое число. Чтобы установить константу нормализации A = 1, мы добавляем граничное условие:

y'(0) = k

Снова перепишем наше уравнение как систему первого порядка и реализуем вычисление её правой части:

y1' = y2
y2' = -k**2 * y1

>>> def fun(x, y, p):
...     k = p[0]
...     return np.vstack((y[1], -k**2 * y[0]))

Обратите внимание, что параметры p передаются как вектор (с одним элементом в нашем случае).

Реализовать граничные условия:

>>> def bc(ya, yb, p):
...     k = p[0]
...     return np.array([ya[0], yb[0], ya[1] - k])

Настройка начальной сетки и предположения для y. Мы стремимся найти решение для k = 2 * pi, для этого мы устанавливаем значения y примерно следующими sin(2 * pi * x):

>>> x = np.linspace(0, 1, 5)
>>> y = np.zeros((2, x.size))
>>> y[0, 1] = 1
>>> y[0, 3] = -1

Запустите решатель с начальным предположением 6 для k.

>>> sol = solve_bvp(fun, bc, x, y, p=[6])

Мы видим, что найденное k приблизительно верно:

>>> sol.p[0]
6.28329460046

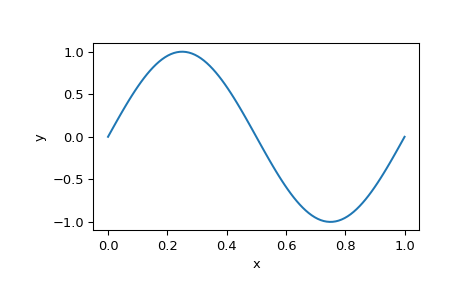
И, наконец, построить график решения, чтобы увидеть ожидаемую синусоиду:

>>> x_plot = np.linspace(0, 1, 100)
>>> y_plot = sol.sol(x_plot)[0]
>>> plt.plot(x_plot, y_plot)
>>> plt.xlabel("x")
>>> plt.ylabel("y")
>>> plt.show()

../../_images/scipy-integrate-solve_bvp-1_01_00.png