scipy.interpolate.LSQBivariateSpline.

ev

LSQBivariateSpline.ev(xi, yi, dx=0, dy=0)

Вычислить сплайн в точках

Возвращает интерполированное значение в (xi[i], yi[i]), i=0,...,len(xi)-1.

Параметры:

xi, yiarray_like

Входные координаты. Соблюдается стандартное правило трансляции Numpy. Порядок осей согласован с np.meshgrid(..., indexing="ij") и несовместимо с порядком по умолчанию np.meshgrid(..., indexing="xy").

dxint, необязательный

Порядок производной по x

Добавлено в версии 0.14.0.

dyint, необязательный

Порядок производной по y

Добавлено в версии 0.14.0.

Примеры

Попробуйте в вашем браузере!

Предположим, что мы хотим билинейно интерполировать экспоненциально затухающую функцию в 2 измерениях.

>>> import numpy as np
>>> from scipy.interpolate import RectBivariateSpline
>>> def f(x, y):
...     return np.exp(-np.sqrt((x / 2) ** 2 + y**2))

Мы производим выборку функции на грубой сетке и настраиваем интерполятор. Обратите внимание, что по умолчанию indexing="xy" meshgrid привело бы к неожиданному (транспонированному) результату после интерполяции.

>>> xarr = np.linspace(-3, 3, 21)
>>> yarr = np.linspace(-3, 3, 21)
>>> xgrid, ygrid = np.meshgrid(xarr, yarr, indexing="ij")
>>> zdata = f(xgrid, ygrid)
>>> rbs = RectBivariateSpline(xarr, yarr, zdata, kx=1, ky=1)

Далее мы семплируем функцию вдоль диагонального среза через координатное пространство на более мелкой сетке с использованием интерполяции.

>>> xinterp = np.linspace(-3, 3, 201)
>>> yinterp = np.linspace(3, -3, 201)
>>> zinterp = rbs.ev(xinterp, yinterp)

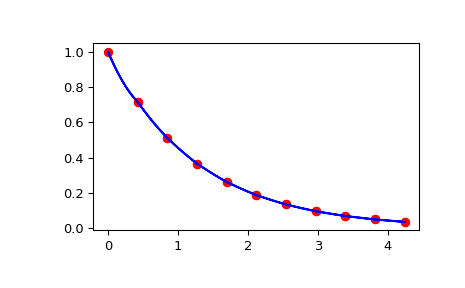
И проверить, что интерполяция проходит через вычисления функции как функция расстояния от начала координат вдоль среза.

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(1, 1, 1)
>>> ax1.plot(np.sqrt(xarr**2 + yarr**2), np.diag(zdata), "or")
>>> ax1.plot(np.sqrt(xinterp**2 + yinterp**2), zinterp, "-b")
>>> plt.show()

НазадОткрыть во вкладке