scipy.interpolate.

krogh_interpolate#

scipy.interpolate.krogh_interpolate(xi, yi, x, der=0, ось=0)[источник]#

Удобная функция для интерполяции Кроу.

См. KroghInterpolator для получения дополнительной информации.

Параметры:

xiarray_like: Точки интерполяции (известные x-координаты).
yiarray_like: Известные y-координаты, формы (xi.size, R). Интерпретируются как векторы длины R или скаляры, если R=1.
xarray_like: Точка или точки, в которых вычисляются производные.
derint или list или None, опционально: Сколько производных вычислить, или None для всех потенциально ненулевых производных (то есть число, равное количеству точек), или список производных для вычисления. Это число включает значение функции как '0-ю' производную.
осьint, необязательный: Ось в yi массив, соответствующий значениям координаты x.

Возвращает:

dndarray: Если значения интерполятора имеют размерность R-D, то возвращаемый массив будет иметь размерность: количество производных на N на R. Если x является скаляром, среднее измерение будет удалено; если yi являются скалярами, то последнее измерение будет удалено.

Смотрите также

KroghInterpolator: Интерполятор Крога

Примечания

Построение интерполяционного полинома — относительно затратный процесс. Если вы хотите вычислять его многократно, рассмотрите использование класса KroghInterpolator (который используется этой функцией).

Примеры

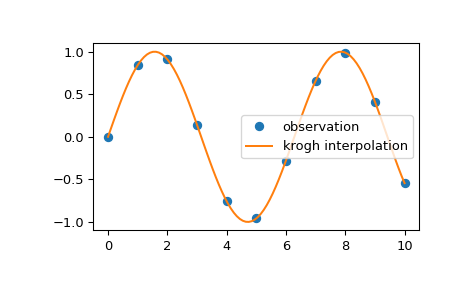
Мы можем интерполировать 2D наблюдаемые данные, используя интерполяцию Крога:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import krogh_interpolate
>>> x_observed = np.linspace(0.0, 10.0, 11)
>>> y_observed = np.sin(x_observed)
>>> x = np.linspace(min(x_observed), max(x_observed), num=100)
>>> y = krogh_interpolate(x_observed, y_observed, x)
>>> plt.plot(x_observed, y_observed, "o", label="observation")
>>> plt.plot(x, y, label="krogh interpolation")
>>> plt.legend()
>>> plt.show()

../../_images/scipy-interpolate-krogh_interpolate-1.png