scipy.optimize.

root#

scipy.optimize.root(fun, x0, args=(), метод='hybr', jac=None, tol=None, callback=None, опции=None)[источник]#

Найти корень векторной функции.

Параметры:

funcallable

Векторная функция для нахождения корня.

Предположим, что вызываемый объект имеет сигнатуру f0(x, *my_args, **my_kwargs), где my_args и my_kwargs являются обязательными позиционными и ключевыми аргументами. Вместо передачи f0 в качестве вызываемого объекта, оберните его, чтобы он принимал только x; например, передать fun=lambda x: f0(x, *my_args, **my_kwargs) как вызываемый объект, где my_args (кортеж) и my_kwargs (dict) были собраны перед вызовом этой функции.

x0ndarray

Начальное приближение.

argsкортеж, необязательный

Дополнительные аргументы, передаваемые в целевую функцию и её якобиан.

методstr, optional

Тип решателя. Должен быть одним из

‘hybr’ (см. здесь)
‘lm’ (см. здесь)
'broyden1' (см. здесь)
'broyden2' (см. здесь)
'anderson' (см. здесь)
'linearmixing' (см. здесь)
‘diagbroyden’ (см. здесь)
‘excitingmixing’ (см. здесь)
'krylov' (см. здесь)
'df-sane' (см. здесь)

jacbool или callable, необязательно

Если jac является логическим значением и равно True, fun предполагается, что возвращает значение матрицы Якоби вместе с целевой функцией. Если False, матрица Якоби будет оценена численно. jac также может быть вызываемым объектом, возвращающим якобиан fun. В этом случае он должен принимать те же аргументы, что и fun.

tolfloat, опционально

Допуск для завершения. Для детального управления используйте специфичные для решателя опции.

callbackфункция, необязательный

Необязательная функция обратного вызова. Она вызывается на каждой итерации как callback(x, f) где x является текущим решением и f соответствующий остаток. Для всех методов, кроме 'hybr' и 'lm'.

опцииdict, optional

Словарь опций решателя. Например, xtol или maxiter, см. show_options() подробности.

Возвращает:

solOptimizeResult: Решение представлено как OptimizeResult объект. Важные атрибуты: x массив решения, success логический флаг, указывающий, завершился ли алгоритм успешно, и message который описывает причину завершения. См. OptimizeResult для описания других атрибутов.

Смотрите также

show_options: Дополнительные параметры, принимаемые решателями

Примечания

Этот раздел описывает доступные решатели, которые можно выбрать с помощью параметра 'method'. Метод по умолчанию — hybr.

Метод hybr использует модификацию гибридного метода Пауэлла, реализованного в MINPACK [1].

Метод lm решает систему нелинейных уравнений в смысле наименьших квадратов, используя модификацию алгоритма Левенберга-Марквардта, реализованную в MINPACK [1].

Метод df-sane является спектральным методом без производных. [3]

Методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, крилов являются неточными методами Ньютона, с возвратом или полным поиском по линии [2]. Каждый метод соответствует определённому приближению Якобиана.

Метод broyden1 использует первое приближение Якобиана Бройдена, это известно как хороший метод Бройдена.
Метод broyden2 использует второе приближение Якобиана Бройдена, оно известно как плохой метод Бройдена.
Метод anderson использует (расширенное) смешивание Андерсона.
Метод Крылов использует приближение Крылова для обратной матрицы Якоби. Это подходит для крупномасштабных задач.
Метод diagbroyden использует диагональное приближение Якобиана Бройдена.
Метод linearmixing использует скалярное приближение Якобиана.
Метод excitingmixing использует настроенную диагональную аппроксимацию Якобиана.

Предупреждение

Алгоритмы, реализованные для методов diagbroyden, linearmixing и excitingmixing может быть полезно для конкретных задач, но их работоспособность может сильно зависеть от проблемы.

Добавлено в версии 0.11.0.

Ссылки

[1] (1,2)

Мор, Хорхе Дж., Бертон С. Гарбоу и Кеннет Э. Хиллстром. 1980. Руководство пользователя для MINPACK-1.

[2]

C. T. Kelley. 1995. Iterative Methods for Linear and Nonlinear Equations. Society for Industrial and Applied Mathematics. <https://archive.siam.org/books/kelley/fr16/>

[3]

La Cruz, J.M. Martinez, M. Raydan. Math. Comp. 75, 1429 (2006).

Примеры

Следующие функции определяют систему нелинейных уравнений и ее якобиан.

>>> import numpy as np
>>> def fun(x):
...     return [x[0]  + 0.5 * (x[0] - x[1])**3 - 1.0,
...             0.5 * (x[1] - x[0])**3 + x[1]]

>>> def jac(x):
...     return np.array([[1 + 1.5 * (x[0] - x[1])**2,
...                       -1.5 * (x[0] - x[1])**2],
...                      [-1.5 * (x[1] - x[0])**2,
...                       1 + 1.5 * (x[1] - x[0])**2]])

Решение может быть получено следующим образом.

>>> from scipy import optimize
>>> sol = optimize.root(fun, [0, 0], jac=jac, method='hybr')
>>> sol.x
array([ 0.8411639,  0.1588361])

Большая задача

Предположим, что нам нужно решить следующее интегродифференциальное уравнение на квадрате \([0,1]\times[0,1]\):

\[\nabla^2 P = 10 \left(\int_0^1\int_0^1\cosh(P)\,dx\,dy\right)^2\]

с \(P(x,1) = 1\) и \(P=0\) в других местах на границе квадрата.

Решение может быть найдено с использованием method='krylov' solver:

>>> from scipy import optimize
>>> # parameters
>>> nx, ny = 75, 75
>>> hx, hy = 1./(nx-1), 1./(ny-1)

>>> P_left, P_right = 0, 0
>>> P_top, P_bottom = 1, 0

>>> def residual(P):
...    d2x = np.zeros_like(P)
...    d2y = np.zeros_like(P)
...
...    d2x[1:-1] = (P[2:]   - 2*P[1:-1] + P[:-2]) / hx/hx
...    d2x[0]    = (P[1]    - 2*P[0]    + P_left)/hx/hx
...    d2x[-1]   = (P_right - 2*P[-1]   + P[-2])/hx/hx
...
...    d2y[:,1:-1] = (P[:,2:] - 2*P[:,1:-1] + P[:,:-2])/hy/hy
...    d2y[:,0]    = (P[:,1]  - 2*P[:,0]    + P_bottom)/hy/hy
...    d2y[:,-1]   = (P_top   - 2*P[:,-1]   + P[:,-2])/hy/hy
...
...    return d2x + d2y - 10*np.cosh(P).mean()**2

>>> guess = np.zeros((nx, ny), float)
>>> sol = optimize.root(residual, guess, method='krylov')
>>> print('Residual: %g' % abs(residual(sol.x)).max())
Residual: 5.7972e-06  # may vary

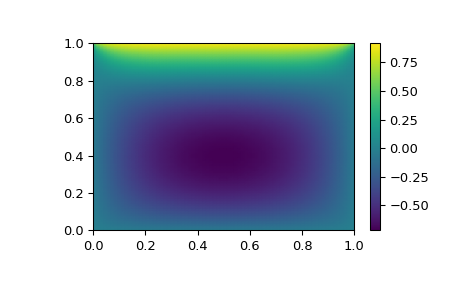
>>> import matplotlib.pyplot as plt
>>> x, y = np.mgrid[0:1:(nx*1j), 0:1:(ny*1j)]
>>> plt.pcolormesh(x, y, sol.x, shading='gouraud')
>>> plt.colorbar()
>>> plt.show()