scipy.signal.

cspline1d_eval

scipy.signal.cspline1d_eval(cj, newx, dx=1.0, x0=0)

Вычислить кубический сплайн в новом наборе точек.

dx является старым шагом дискретизации, в то время как x0 был старым началом. Другими словами, старые точки выборки (узловые точки), для которых cj представляли коэффициенты сплайна в равноотстоящих точках:

oldx = x0 + j*dx j=0…N-1, где N=len(cj)

Края обрабатываются с использованием зеркально-симметричных граничных условий.

Параметры:

cjndarray

коэффициенты кубического сплайна

newxndarray

Новый набор точек.

dxfloat, опционально

Старый интервал между выборками, значение по умолчанию равно 1.0.

x0int, необязательный

Старое начало, значение по умолчанию - 0.

Возвращает:

resndarray

Вычисление точек кубического сплайна.

Смотрите также

cspline1d

Вычислить коэффициенты кубического сплайна для массива ранга 1.

Примеры

Попробуйте в вашем браузере!

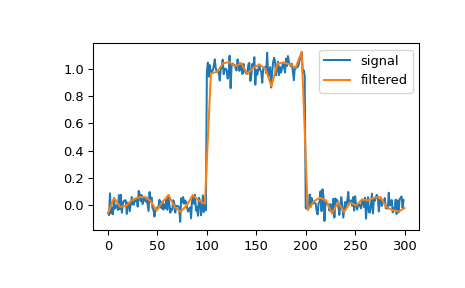
Мы можем фильтровать сигнал, чтобы уменьшить и сгладить высокочастотный шум с помощью кубического сплайна:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import cspline1d, cspline1d_eval
>>> rng = np.random.default_rng()
>>> sig = np.repeat([0., 1., 0.], 100)
>>> sig += rng.standard_normal(len(sig))*0.05  # add noise
>>> time = np.linspace(0, len(sig))
>>> filtered = cspline1d_eval(cspline1d(sig), time)
>>> plt.plot(sig, label="signal")
>>> plt.plot(time, filtered, label="filtered")
>>> plt.legend()
>>> plt.show()

НазадОткрыть во вкладке