scipy.signal.

filtfilt#

scipy.signal.filtfilt(b, a, x, ось=-1, padtype='odd', padlen=None, метод='pad', irlen=None)[источник]#

Применение цифрового фильтра вперед и назад к сигналу.

Эта функция применяет линейный цифровой фильтр дважды: сначала в прямом направлении, а затем в обратном. Комбинированный фильтр имеет нулевую фазу и порядок фильтра, вдвое превышающий исходный.

Функция предоставляет опции для обработки краев сигнала.

Функция sosfiltfilt (и проектирование фильтров с использованием output='sos') следует предпочесть filtfilt для большинства задач фильтрации, так как секции второго порядка имеют меньше численных проблем.

Параметры:

b(N,) array_like: Вектор коэффициентов числителя фильтра.
a(N,) array_like: Вектор коэффициентов знаменателя фильтра. Если a[0] не равно 1, то оба a и b нормализуются по a[0].
xarray_like: Массив данных для фильтрации.
осьint, необязательный: Ось x к которому применяется фильтр. По умолчанию -1.
padtypestr или None, опционально: Должно быть ‘odd’, ‘even’, ‘constant’ или None. Это определяет тип расширения для дополненного сигнала, к которому применяется фильтр. Если padtype равно None, заполнение не используется. По умолчанию 'odd'.
padlenint или None, опционально: Количество элементов, на которое нужно расширить x на обоих концах ось перед применением фильтра. Это значение должно быть меньше x.shape[axis] - 1. padlen=0 подразумевает отсутствие заполнения. Значение по умолчанию: 3 * max(len(a), len(b)).
методstr, optional: Определяет метод обработки краёв сигнала: либо "pad", либо "gust". Когда метод равно 'pad', сигнал дополняется; тип дополнения определяется padtype и padlen, и irlen игнорируется. Когда метод если "gust", используется метод Густафссона, и padtype и padlen игнорируются.
irlenint или None, опционально: Когда метод является “gust”, irlen определяет длину импульсной характеристики фильтра. Если irlen равно None, никакая часть импульсной характеристики не игнорируется. Для длинного сигнала указание irlen может значительно улучшить производительность фильтра.

Возвращает:

yndarray: Отфильтрованный вывод с той же формой, что и x.

Смотрите также

sosfiltfilt, lfilter_zi, lfilter, lfiltic, savgol_filter, sosfilt

Примечания

Когда метод это “pad”, функция дополняет данные вдоль заданной оси одним из трех способов: нечетным, четным или постоянным. Нечетное и четное расширения имеют соответствующую симметрию относительно конечной точки данных. Постоянное расширение дополняет данные значениями в конечных точках. На прямом и обратном проходах начальное условие фильтра находится с использованием lfilter_zi и масштабирование конечной точкой расширенных данных.

Когда метод это "gust", метод Густафссона [1] используется. Начальные условия выбираются для прямого и обратного проходов так, чтобы прямо-обратный фильтр давал тот же результат, что и обратно-прямой фильтр.

Опция использования метода Густаффсона была добавлена в версии scipy 0.16.0.

Ссылки

[1]

F. Gustaffson, "Определение начальных состояний в прямом-обратном фильтровании", Transactions on Signal Processing, Vol. 46, pp. 988-992, 1996.

Примеры

В примерах будут использоваться несколько функций из scipy.signal.

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

Сначала создадим однсекундный сигнал, который является суммой двух чистых синусоидальных волн с частотами 5 Гц и 250 Гц, дискретизированными на 2000 Гц.

>>> t = np.linspace(0, 1.0, 2001)
>>> xlow = np.sin(2 * np.pi * 5 * t)
>>> xhigh = np.sin(2 * np.pi * 250 * t)
>>> x = xlow + xhigh

Теперь создайте фильтр Баттерворта нижних частот с частотой среза 0.125 от частоты Найквиста, или 125 Гц, и примените его к x с filtfilt. Результат должен быть приблизительно xlow, без фазового сдвига.

>>> b, a = signal.butter(8, 0.125)
>>> y = signal.filtfilt(b, a, x, padlen=150)
>>> np.abs(y - xlow).max()
9.1086182074789912e-06

Мы получаем довольно чистый результат для этого искусственного примера, потому что нечётное расширение точное, и при умеренно длинном дополнении переходные процессы фильтра рассеиваются к моменту достижения фактических данных. В общем случае переходные эффекты на краях неизбежны.

Следующий пример демонстрирует опцию method="gust".

Сначала создайте фильтр.

>>> b, a = signal.ellip(4, 0.01, 120, 0.125)  # Filter to be applied.

sig является случайным входным сигналом для фильтрации.

>>> rng = np.random.default_rng()
>>> n = 60
>>> sig = rng.standard_normal(n)**3 + 3*rng.standard_normal(n).cumsum()

Apply filtfilt to sig, один раз с использованием метода Густафссона, и один раз с использованием дополнения, и построение графиков результатов для сравнения.

>>> fgust = signal.filtfilt(b, a, sig, method="gust")
>>> fpad = signal.filtfilt(b, a, sig, padlen=50)
>>> plt.plot(sig, 'k-', label='input')
>>> plt.plot(fgust, 'b-', linewidth=4, label='gust')
>>> plt.plot(fpad, 'c-', linewidth=1.5, label='pad')
>>> plt.legend(loc='best')
>>> plt.show()

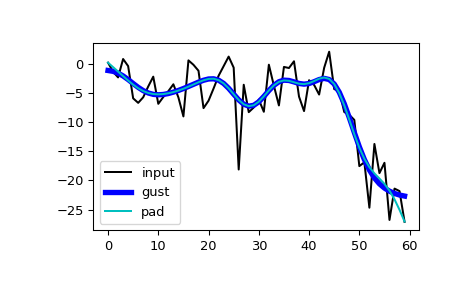
../../_images/scipy-signal-filtfilt-1_00_00.png

The irlen аргумент может быть использован для улучшения производительности метода Густафссона.

Оценить длину импульсной характеристики фильтра.

>>> z, p, k = signal.tf2zpk(b, a)
>>> eps = 1e-9
>>> r = np.max(np.abs(p))
>>> approx_impulse_len = int(np.ceil(np.log(eps) / np.log(r)))
>>> approx_impulse_len
137

Применить фильтр к более длинному сигналу, с и без irlen аргумент. Разница между y1 и y2 невелик. Для длинных сигналов использование irlen дает значительное улучшение производительности.

>>> x = rng.standard_normal(4000)
>>> y1 = signal.filtfilt(b, a, x, method='gust')
>>> y2 = signal.filtfilt(b, a, x, method='gust', irlen=approx_impulse_len)
>>> print(np.max(np.abs(y1 - y2)))
2.875334415008979e-10