scipy.signal.

max_len_seq#

scipy.signal.max_len_seq(nbits, состояние=None, длина=None, taps=None)[источник]#

Генератор максимальной длины последовательности (MLS).

Параметры:

nbitsint: Количество бит для использования. Длина результирующей последовательности будет (2**nbits) - 1. Обратите внимание, что генерация длинных последовательностей (например, больше чем nbits == 16) может занимать много времени.
состояниеarray_like, необязательный: Если массив, должен иметь длину nbits, и будут приведены к бинарному (bool) представлению. Если None, будет использовано начальное значение из единиц, дающее повторяемое представление. Если state состоит из нулей, возникает ошибка, так как это недопустимо. По умолчанию: None.
длинаint, необязательный: Количество выборок для вычисления. Если None, вся длина (2**nbits) - 1 вычисляется.
tapsarray_like, необязательный: Коэффициенты полинома для использования (например, [7, 6, 1] для 8-битной последовательности). Если None, отводы будут выбраны автоматически (для до nbits == 32).

Возвращает:

seqмассив: Результирующая MLS-последовательность из 0 и 1.
состояниемассив: Финальное состояние регистра сдвига.

Примечания

Алгоритм генерации MLS в общем виде описан в:

https://en.wikipedia.org/wiki/Maximum_length_sequence

Значения по умолчанию для taps специально взяты из первого варианта, перечисленного для каждого значения nbits в:

https://web.archive.org/web/20181001062252/http://www.newwaveinstruments.com/resources/articles/m_sequence_linear_feedback_shift_register_lfsr.htm

Добавлено в версии 0.15.0.

Примеры

MLS использует двоичное соглашение:

>>> from scipy.signal import max_len_seq
>>> max_len_seq(4)[0]
array([1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0], dtype=int8)

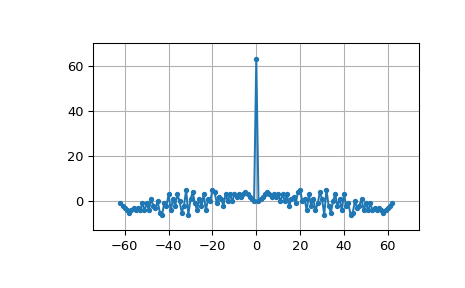
MLS имеет белый спектр (кроме постоянной составляющей):

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from numpy.fft import fft, ifft, fftshift, fftfreq
>>> seq = max_len_seq(6)[0]*2-1  # +1 and -1
>>> spec = fft(seq)
>>> N = len(seq)
>>> plt.plot(fftshift(fftfreq(N)), fftshift(np.abs(spec)), '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

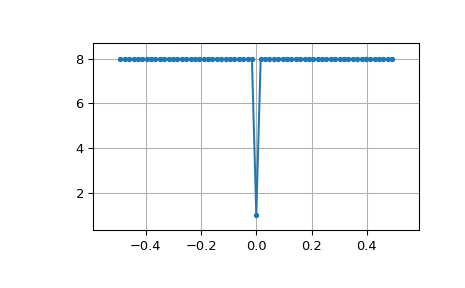
../../_images/scipy-signal-max_len_seq-1_00_00.png

Круговая автокорреляция MLS является импульсом:

>>> acorrcirc = ifft(spec * np.conj(spec)).real
>>> plt.figure()
>>> plt.plot(np.arange(-N/2+1, N/2+1), fftshift(acorrcirc), '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

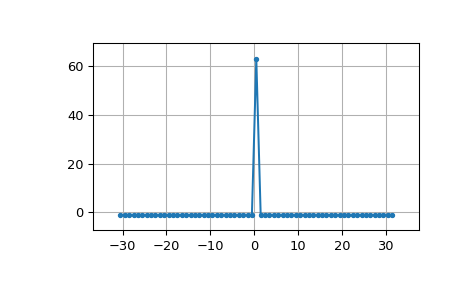
../../_images/scipy-signal-max_len_seq-1_01_00.png

Линейная автокорреляция MLS приблизительно является импульсом:

>>> acorr = np.correlate(seq, seq, 'full')
>>> plt.figure()
>>> plt.plot(np.arange(-N+1, N), acorr, '.-')
>>> plt.margins(0.1, 0.1)
>>> plt.grid(True)
>>> plt.show()

../../_images/scipy-signal-max_len_seq-1_02_00.png