scipy.signal.

peak_prominences#

scipy.signal.peak_prominences(x, пики, wlen=None)[источник]#

Вычислить значимость каждого пика в сигнале.

Выдающаяся вершина (prominence) измеряет, насколько вершина выделяется на фоне окружающего базового уровня сигнала, и определяется как вертикальное расстояние между вершиной и её самой низкой контурной линией.

Параметры:

xпоследовательность: Сигнал с пиками.
пикипоследовательность: Индексы пиков в x.
wlenint, необязательный: Длина окна в выборках, которая опционально ограничивает оцениваемую область для каждого пика подмножеством x. Пик всегда размещается в середине окна, поэтому заданная длина округляется до следующего нечётного целого числа. Этот параметр может ускорить вычисление (см. Примечания).

Возвращает:

выступыndarray: Рассчитанные значения выступа для каждого пика в пики.
left_bases, right_basesndarray: Основания пиков как индексы в x слева и справа от каждого пика. Более высокое основание каждой пары — это самая низкая контурная линия пика.

Вызывает:

ValueError: Если значение в пики является недопустимым индексом для x.

Предупреждает:

PeakPropertyWarning: Для индексов в пики которые не указывают на действительные локальные максимумы в x, возвращаемое значение выступа будет 0, и выводится это предупреждение. Это также происходит, если wlen меньше, чем размер плато пика.

Предупреждение

Эта функция может возвращать неожиданные результаты для данных, содержащих NaN. Чтобы избежать этого, NaN следует либо удалить, либо заменить.

Смотрите также

find_peaks: Найти пики внутри сигнала на основе свойств пиков.
peak_widths: Вычислить ширину пиков.

Примечания

Стратегия вычисления значимости пика:

Продлите горизонтальную линию от текущего пика влево и вправо до тех пор, пока линия либо достигнет границы окна (см. wlen) или пересекает сигнал снова на наклоне более высокого пика. Пересечение с пиком той же высоты игнорируется.
С каждой стороны найти минимальное значение сигнала в интервале, определенном выше. Эти точки являются основаниями пика.
Более высокая из двух баз отмечает нижнюю контурную линию пика. Затем выдающуюся часть можно рассчитать как вертикальную разницу между высотой самого пика и его нижней контурной линией.

Поиск оснований пиков может быть медленным для больших x с периодическим поведением, потому что большие блоки или даже весь сигнал должны быть вычислены для первого шага алгоритма. Эта область вычислений может быть ограничена с помощью параметра wlen что ограничивает алгоритм окном вокруг текущего пика и может сократить время вычислений, если длина окна мала по отношению к x. Однако это может помешать алгоритму найти истинную глобальную контурную линию, если истинные основания пика находятся за пределами этого окна. Вместо этого, более высокая контурная линия находится в пределах ограниченного окна, что приводит к меньшей рассчитанной значимости. На практике это актуально только для самого высокого набора пиков в x. Это поведение может даже использоваться намеренно для вычисления "локальных" выступов.

Добавлено в версии 1.1.0.

Ссылки

[1]

Статья в Википедии о топографической выдаче: https://en.wikipedia.org/wiki/Topographic_prominence

Примеры

>>> import numpy as np
>>> from scipy.signal import find_peaks, peak_prominences
>>> import matplotlib.pyplot as plt

Создать тестовый сигнал с двумя наложенными гармониками

>>> x = np.linspace(0, 6 * np.pi, 1000)
>>> x = np.sin(x) + 0.6 * np.sin(2.6 * x)

Найти все пики и вычислить их значимость

>>> peaks, _ = find_peaks(x)
>>> prominences = peak_prominences(x, peaks)[0]
>>> prominences
array([1.24159486, 0.47840168, 0.28470524, 3.10716793, 0.284603  ,
       0.47822491, 2.48340261, 0.47822491])

Вычислите высоту контурной линии каждого пика и постройте результаты

>>> contour_heights = x[peaks] - prominences
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.vlines(x=peaks, ymin=contour_heights, ymax=x[peaks])
>>> plt.show()

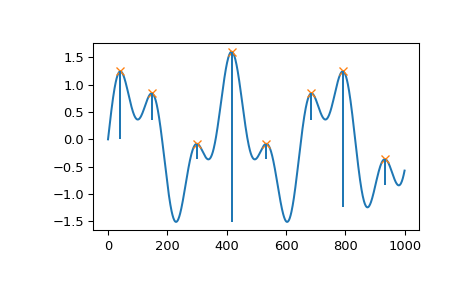
../../_images/scipy-signal-peak_prominences-1_00_00.png

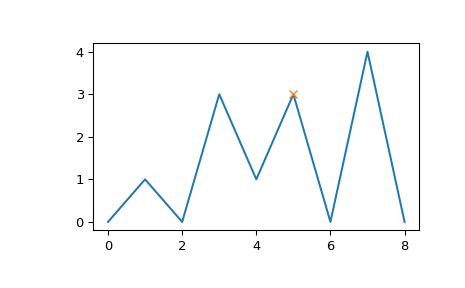
Давайте оценим второй пример, который демонстрирует несколько крайних случаев для одного пика на индексе 5.

>>> x = np.array([0, 1, 0, 3, 1, 3, 0, 4, 0])
>>> peaks = np.array([5])
>>> plt.plot(x)
>>> plt.plot(peaks, x[peaks], "x")
>>> plt.show()

../../_images/scipy-signal-peak_prominences-1_01_00.png

>>> peak_prominences(x, peaks)  # -> (prominences, left_bases, right_bases)
(array([3.]), array([2]), array([6]))

Обратите внимание, как пик с индексом 3 той же высоты не считается границей при поиске левого основания. Вместо этого находятся два минимума в 0 и 2, в этом случае всегда выбирается тот, который ближе к оцениваемому пику. С правой стороны, однако, основание должно быть размещено в 6, потому что более высокий пик представляет правую границу оцениваемой области.

>>> peak_prominences(x, peaks, wlen=3.1)
(array([2.]), array([4]), array([6]))

Здесь мы ограничили алгоритм окном от 3 до 7 (длина составляет 5 выборок, потому что wlen было округлено до следующего нечётного целого числа). Таким образом, единственными двумя кандидатами в оцениваемой области являются два соседних образца, и вычисляется меньшая значимость.