scipy.signal.

resample

scipy.signal.resample(x, число, t=None, ось=0, window=None, область определения='time')

Resample x to число выборки с использованием метода Фурье вдоль заданной ось.

Передискретизация выполняется путем укорачивания или дополнения нулями БПФ x. Это имеет преимущества предоставления идеального антиалиасингового фильтра и позволяет использовать произвольные коэффициенты повышения или понижения частоты дискретизации. Основным недостатком является требование предположения x является периодическим сигналом.

Параметры:

xarray_like

Входной сигнал, состоящий из равноотстоящих выборок. Если x является многомерным массивом, параметр ось определяет ось времени/частоты. Предполагается, что здесь n_x = x.shape[axis] определяет количество выборок и T интервал выборки.

числоint

Количество сэмплов ресемплированного выходного сигнала. Оно может быть больше или меньше, чем n_x.

tarray_like, необязательный

Если t не является None, тогда временные метки передискретизированного сигнала также возвращаются. t должен содержать как минимум первые две временные метки входного сигнала x (все остальные игнорируются). Временные метки выходного сигла определяются t[0] + T * n_x / num * np.arange(num) с T = t[1] - t[0]. По умолчанию None.

осьint, необязательный

Ось времени/частоты x вдоль которого происходит передискретизация. По умолчанию 0.

windowarray_like, callable, string, float, или tuple, optional

Если не None, он задаёт фильтр в частотной области, который применяется перед передискретизацией. Т.е., БПФ X of x вычисляется по X = W * fft(x, axis=axis). W может интерпретироваться как функция спектрального оконного преобразования W(f_X) который использует частоты f_X = fftfreq(n_x, T).

Если window является одномерным массивом длины n_x затем W=window. Если window является вызываемым объектом, тогда W = window(f_X). В противном случае, window передаётся в get_window, т.е., W = fftshift(signal.get_window(window, n_x)). По умолчанию None.

область определения'time' | 'freq', опционально

Если установлено в 'time' (по умолчанию) затем применяется БПФ к x, иначе ('freq') предполагается, что БПФ уже было применено, т.е., x = fft(x_t, axis=axis) с x_t является входным сигналом во временной области.

Возвращает:

x_rndarray

Передискретизированный сигнал, состоящий из число выборки и интервал выборки T * n_x / num.

t_rndarray, необязательно

The число равноотстоящие временные метки x_r. Это возвращается только если параметр t не является None.

Смотрите также

decimate

Понизьте частоту дискретизации (периодического/непериодического) сигнала после применения FIR или IIR фильтра.

resample_poly

Передискретизировать (периодический/непериодический) сигнал с использованием полифазной фильтрации и КИХ-фильтра.

Примечания

Эта функция использует более эффективное одностороннее БПФ, т.е. rfft / irfft, если x является вещественнозначным и во временной области. В противном случае, двустороннее БПФ, т.е., fft / ifft, используется (все функции БПФ взяты из scipy.fft модуль).

Если window применяется к вещественному x, односторонняя спектральная оконная функция определяется путём усреднения отрицательной и положительной частотной компоненты. Это гарантирует, что вещественные сигналы и комплексные сигналы с нулевой мнимой частью обрабатываются одинаково. Т.е., передача x или передача x.astype(np.complex128) дают одинаковый численный результат.

Если количество входных или выходных выборок является простым числом или имеет мало простых делителей, эта функция может быть медленной из-за использования БПФ. Обратитесь к prev_fast_len и next_fast_len для определения эффективных длин сигналов. В качестве альтернативы, использование resample_poly вычисление промежуточного сигнала (как проиллюстрировано в примере ниже) может привести к значительному увеличению скорости.

resample предназначен для использования с периодическими сигналами с равномерными интервалами выборки. Для непериодических сигналов, resample_poly может быть лучшим выбором. Обратитесь к scipy.interpolate модуль для методов передискретизации сигналов с непостоянными интервалами выборки.

Примеры

Попробуйте в вашем браузере!

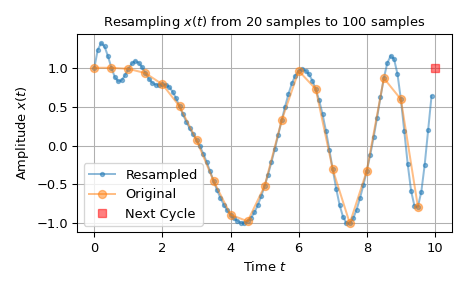
Следующий пример показывает сигнал, подвергнутый увеличению частоты дискретизации с 20 отсчётов до 100 отсчётов. Звон в начале сигнала с увеличенной частотой дискретизации возникает из-за интерпретации сигнала как периодического. Красный квадрат на графике иллюстрирует эту периодичность, показывая первый отсчёт следующего цикла сигнала.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import resample
...
>>> n0, n1 = 20, 100  # number of samples
>>> t0 = np.linspace(0, 10, n0, endpoint=False)  # input time stamps
>>> x0 = np.cos(-t0**2/6)  # input signal
...
>>> x1 = resample(x0, n1)  # resampled signal
>>> t1 = np.linspace(0, 10, n1, endpoint=False)  # timestamps of x1
...
>>> fig0, ax0 = plt.subplots(1, 1, tight_layout=True)
>>> ax0.set_title(f"Resampling $x(t)$ from {n0} samples to {n1} samples")
>>> ax0.set(xlabel="Time $t$", ylabel="Amplitude $x(t)$")
>>> ax0.plot(t1, x1, '.-', alpha=.5, label=f"Resampled")
>>> ax0.plot(t0, x0, 'o-', alpha=.5, label="Original")
>>> ax0.plot(10, x0[0], 'rs', alpha=.5, label="Next Cycle")
>>> ax0.legend(loc='best')
>>> ax0.grid(True)
>>> plt.show()

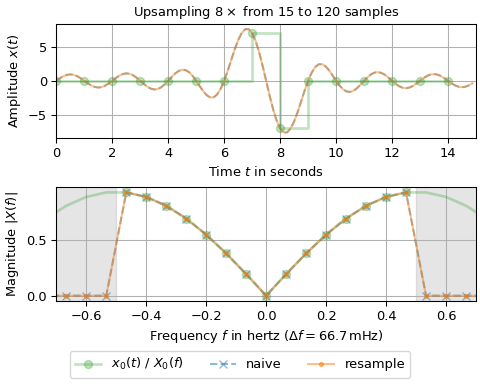
Следующий пример сравнивает эту функцию с наивным rfft / irfft комбинация: Входной сигнал с интервалом дискретизации в одну секунду повышается в восемь раз. Первый рисунок изображает нечётное число входных выборок, а второй — чётное. Верхние подграфики показывают сигналы во времени: входные выборки отмечены большими зелёными точками, повышенные сигналы — сплошной и пунктирной линиями. Нижние подграфики показывают амплитудный спектр: значения БПФ входа изображены большими зелёными точками, которые лежат в частотном интервале [-0.5, 0.5] Гц, тогда как частотный интервал повышенного сигнала — [-4, 4] Гц. Сплошная зелёная линия изображает повышенный спектр без антиалиасингового фильтра, который является периодическим продолжением входного спектра. Синие крестики и оранжевые точки изображают значения БПФ сигнала, созданного наивным подходом, а также результат этой функции.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.fft import fftshift, fftfreq, fft, rfft, irfft
>>> from scipy.signal import resample, resample_poly
... 
>>> fac, T0, T1 = 8, 1, 1/8  # upsampling factor and sampling intervals
>>> for n0 in (15, 16):  # number of samples of input signal
...     n1 = fac * n0  # number of samples of upsampled signal
...     t0, t1 = T0 * np.arange(n0), T1 * np.arange(n1)  # time stamps
...     x0 = np.zeros(n0)  # input signal has two non-zero sample values
...     x0[n0//2], x0[n0//2+1] = n0 // 2, -(n0 // 2)
... 
...     x1n = irfft(rfft(x0), n=n1) * n1 / n0  # naive resampling
...     x1r = resample(x0, n1)  # resample signal
... 
...     # Determine magnitude spectrum:
...     x0_up = np.zeros_like(x1r)  # upsampling without antialiasing filter
...     x0_up[::n1 // n0] = x0
...     X0, X0_up = (fftshift(fft(x_)) / n0 for x_ in (x0, x0_up))
...     XX1 = (fftshift(fft(x_)) / n1 for x_ in (x1n, x1r))
...     f0, f1 = fftshift(fftfreq(n0, T0)), fftshift(fftfreq(n1, T1))  # frequencies
...     df = f0[1] - f0[0]  # frequency resolution
... 
...     fig, (ax0, ax1) = plt.subplots(2, 1, layout='constrained', figsize=(5, 4))
...     ax0.set_title(rf"Upsampling ${fac}\times$ from {n0} to {n1} samples")
...     ax0.set(xlabel="Time $t$ in seconds", ylabel="Amplitude $x(t)$", 
...             xlim=(0, n1*T1))
...     ax0.step(t0, x0, 'C2o-', where='post', alpha=.3, linewidth=2, 
...              label="$x_0(t)$ / $X_0(f)$")
...     for x_, l_ in zip((x1n, x1r), ('C0--', 'C1-')):
...         ax0.plot(t1, x_, l_, alpha=.5, label=None)
...     ax0.grid()
...     ax1.set(xlabel=rf"Frequency $f$ in hertz ($\Delta f = {df*1e3:.1f}\,$mHz)", 
...             ylabel="Magnitude $|X(f)|$", xlim=(-0.7, 0.7))
...     ax1.axvspan(0.5/T0, f1[-1], color='gray', alpha=.2)
...     ax1.axvspan(f1[0], -0.5/T0, color='gray', alpha=.2)
...     ax1.plot(f1, abs(X0_up), 'C2-', f0, abs(X0),  'C2o', alpha=.3, linewidth=2)
...     for X_, n_, l_ in zip(XX1, ("naive", "resample"), ('C0x--', 'C1.-')): 
...         ax1.plot(f1, abs(X_), l_, alpha=.5, label=n_)
...     ax1.grid()
...     fig.legend(loc='outside lower center', ncols=4)    
>>> plt.show()

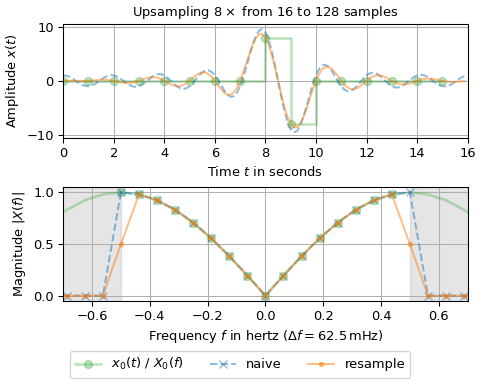
Первая фигура показывает, что повышение частоты дискретизации нечётного числа выборок даёт идентичные результаты. Вторая фигура иллюстрирует, что сигнал, созданный с помощью наивного подхода (пунктирная синяя линия) из чётного числа выборок, не проходит через все исходные выборки. Это отклонение связано с resample correctly treating unpaired frequency bins. I.e., the input x1 имеет пару бинов ±0.5 Гц, тогда как выход имеет только один непарный бин на -0.5 Гц, что требует перемасштабирования этой пары бинов. В общем случае, специальная обработка требуется, если n_x != num и min(n_x, num) чётное. Если значения бинов в ±m равны нулю, очевидно, специальная обработка не требуется. Обратитесь к исходному коду resample подробности.

Последний пример показывает, как использовать resample_poly для ускорения понижающей дискретизации: Входной сигнал имеет ненулевое значение в \(t=0\) и понижается с 19937 до 128 выборок. Поскольку 19937 является простым числом, ожидается, что БПФ будет медленным. Чтобы ускорить процесс, resample_poly используется для первоначального понижения дискретизации с коэффициентом n0 // n1 = 155 а затем передать результат в resample. Две параметризации resample_poly используются: Передача padtype='wrap' рассматривает входные данные как периодические, тогда как параметризация по умолчанию выполняет дополнение нулями. Верхний график показывает результирующие сигналы во времени, а нижний график изображает результирующие односторонние амплитудные спектры.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.fft import rfftfreq, rfft
>>> from scipy.signal import resample, resample_poly
... 
>>> n0 = 19937 # number of input samples - prime
>>> n1 = 128  # number of output samples - fast FFT length
>>> T0, T1 = 1/n0, 1/n1  # sampling intervals
>>> t0, t1 = np.arange(n0)*T0, np.arange(n1)*T1  # time stamps
... 
>>> x0 = np.zeros(n0)  # Input has one non-zero sample
>>> x0[0] = n0
>>> 
>>> x1r = resample(x0, n1)  # slow due to n0 being prime
>>> # This is faster:
>>> x1p = resample(resample_poly(x0, 1, n0 // n1, padtype='wrap'), n1)  # periodic 
>>> x2p = resample(resample_poly(x0, 1, n0 // n1), n1)  # with zero-padding
... 
>>> X0 = rfft(x0) / n0 
>>> X1r, X1p, X2p = rfft(x1r) / n1, rfft(x1p) / n1, rfft(x2p) / n1
>>> f0, f1 = rfftfreq(n0, T0), rfftfreq(n1, T1)
... 
>>> fig, (ax0, ax1) = plt.subplots(2, 1, layout='constrained', figsize=(5, 4))
>>> ax0.set_title(f"Dowsampled Impulse response (from {n0} to {n1} samples)")
>>> ax0.set(xlabel="Time $t$ in seconds", ylabel="Amplitude $x(t)$", xlim=(-T1, 1)) 
>>> for x_ in (x1r, x1p, x2p):
...     ax0.plot(t1, x_, alpha=.5)
>>> ax0.grid()
>>> ax1.set(xlabel=rf"Frequency $f$ in hertz ($\Delta f = {f1[1]}\,$Hz)", 
...         ylabel="Magnitude $|X(f)|$", xlim=(0, 0.55/T1))
>>> ax1.axvspan(0.5/T1, f0[-1], color='gray', alpha=.2)
>>> ax1.plot(f1, abs(X1r), 'C0.-', alpha=.5, label="resample")
>>> ax1.plot(f1, abs(X1p), 'C1.-', alpha=.5, label="resample_poly(padtype='wrap')")
>>> ax1.plot(f1, abs(X2p), 'C2x-', alpha=.5, label="resample_poly")
>>> ax1.grid()
>>> fig.legend(loc='outside lower center', ncols=2)
>>> plt.show()    

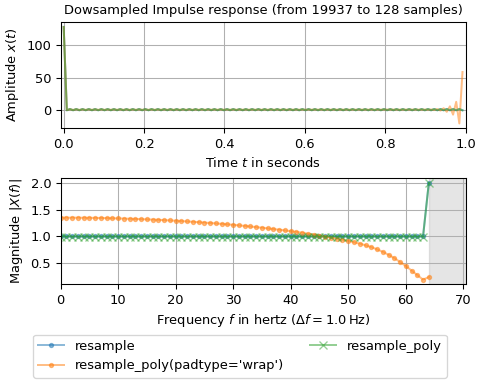
Графики показывают, что результаты "чистого" resample и использование параметров по умолчанию для resample_poly хорошо согласуются. Периодическое дополнение resample_poly (padtype='wrap') с другой стороны даёт значительные отклонения. Это вызвано разрывом в начале сигнала, для которого фильтр по умолчанию resample_poly не подходит хорошо. Этот пример иллюстрирует, что для некоторых случаев использования адаптация resample_poly параметры могут быть полезными. resample имеет большое преимущество в этом отношении: по умолчанию использует идеальный антиалиасинговый фильтр с максимальной полосой пропускания.

Обратите внимание, что удвоенная спектральная величина на частоте Найквиста 64 Гц обусловлена четным числом n1=128 выходные выборки, которые требуют специальной обработки, как обсуждалось в предыдущем примере.

НазадОткрыть во вкладке