scipy.spatial.

HalfspaceIntersection

класс scipy.spatial.HalfspaceIntersection(полупространства, interior_point, инкрементальных=False, qhull_options=None)

Пересечения полупространств в N измерениях.

Добавлено в версии 0.19.0.

Параметры:

полупространстваndarray чисел с плавающей запятой, форма (nineq, ndim+1)

Сложенные неравенства вида Ax + b <= 0 в формате [A; b]

interior_pointndarray из float, форма (ndim,)

Точка, явно находящаяся внутри области, определённой полупространствами. Также называется допустимой точкой, её можно получить с помощью линейного программирования.

инкрементальныхbool, необязательно

Позволяет добавлять новые полупространства инкрементально. Это требует дополнительных ресурсов.

qhull_optionsstr, optional

Дополнительные опции для передачи в Qhull. См. руководство Qhull для подробностей. (По умолчанию: “Qx” для ndim > 4 и “” в противном случае) Опция “H” всегда включена.

Атрибуты:

полупространстваndarray из double, форма (nineq, ndim+1)

Входные полупространства.

interior_point :ndarray из float, форма (ndim,)

Входная внутренняя точка.

пересеченияndarray типа double, форма (ninter, ndim)

Пересечения всех полупространств.

двойные точкиndarray типа double, форма (nineq, ndim)

Двойные точки входных полупространств.

dual_facetsсписок списков целых чисел

Индексы точек, образующих (не обязательно симплициальные) грани двойной выпуклой оболочки.

dual_verticesndarray целых чисел, форма (nvertices,)

Индексы полупространств, образующих вершины двойственной выпуклой оболочки. Для 2-D выпуклых оболочек вершины расположены против часовой стрелки. Для других размерностей они расположены в порядке ввода.

dual_equationsndarray типа double, форма (nfacet, ndim+1)

[normal, offset] формируют уравнение гиперплоскости двойственной грани (см. Документация Qhull для получения дополнительной информации).

dual_areafloat

Площадь двойной выпуклой оболочки

dual_volumefloat

Объем двойного выпуклого многогранника

Методы

add_halfspaces(halfspaces[, restart])	Обработать набор дополнительных новых полупространств.
close()	Завершить инкрементную обработку.

Вызывает:

QhullError

Возникает, когда Qhull сталкивается с ошибкой, например, геометрической вырожденностью, когда опции для разрешения не включены.

ValueError

Возникает, если на вход подается несовместимый массив.

Примечания

Пересечения вычисляются с использованием Библиотека Qhull. Это воспроизводит функциональность «qhalf» Qhull.

Ссылки

[Qhull]

http://www.qhull.org/

[1]

S. Boyd, L. Vandenberghe, Convex Optimization, доступно на http://stanford.edu/~boyd/cvxbook/

Примеры

Попробуйте в вашем браузере!

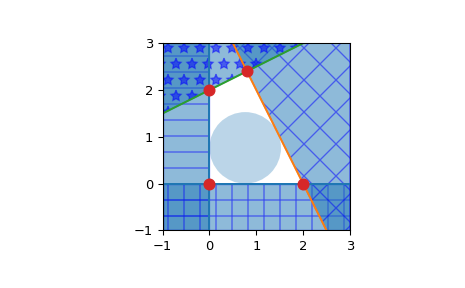
Пересечение полупространств плоскостей, образующих некоторый многоугольник

>>> from scipy.spatial import HalfspaceIntersection
>>> import numpy as np
>>> halfspaces = np.array([[-1, 0., 0.],
...                        [0., -1., 0.],
...                        [2., 1., -4.],
...                        [-0.5, 1., -2.]])
>>> feasible_point = np.array([0.5, 0.5])
>>> hs = HalfspaceIntersection(halfspaces, feasible_point)

Построить полупространства как заполненные области и точки пересечения:

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1, aspect='equal')
>>> xlim, ylim = (-1, 3), (-1, 3)
>>> ax.set_xlim(xlim)
>>> ax.set_ylim(ylim)
>>> x = np.linspace(-1, 3, 100)
>>> symbols = ['-', '+', 'x', '*']
>>> signs = [0, 0, -1, -1]
>>> fmt = {"color": None, "edgecolor": "b", "alpha": 0.5}
>>> for h, sym, sign in zip(halfspaces, symbols, signs):
...     hlist = h.tolist()
...     fmt["hatch"] = sym
...     if h[1]== 0:
...         ax.axvline(-h[2]/h[0], label='{}x+{}y+{}=0'.format(*hlist))
...         xi = np.linspace(xlim[sign], -h[2]/h[0], 100)
...         ax.fill_between(xi, ylim[0], ylim[1], **fmt)
...     else:
...         ax.plot(x, (-h[2]-h[0]*x)/h[1], label='{}x+{}y+{}=0'.format(*hlist))
...         ax.fill_between(x, (-h[2]-h[0]*x)/h[1], ylim[sign], **fmt)
>>> x, y = zip(*hs.intersections)
>>> ax.plot(x, y, 'o', markersize=8)

По умолчанию qhull не предоставляет способ вычисления внутренней точки. Это можно легко вычислить с помощью линейного программирования. Рассматривая полупространства вида \(Ax + b \leq 0\), решая линейную программу:

\[ \begin{align}\begin{aligned}max \: y\\s.t. Ax + y ||A_i|| \leq -b\end{aligned}\end{align} \]

С \(A_i\) являются строками A, т.е. нормалями к каждой плоскости.

Даст точку x, которая наиболее глубоко внутри выпуклого многогранника. Если быть точным, это центр наибольшей гиперсферы радиуса y, вписанной в многогранник. Эта точка называется центром Чебышёва многогранника (см. [1] 4.3.1, стр.148-149). Уравнения, выводимые Qhull, всегда нормализованы.

>>> from scipy.optimize import linprog
>>> from matplotlib.patches import Circle
>>> norm_vector = np.reshape(np.linalg.norm(halfspaces[:, :-1], axis=1),
...     (halfspaces.shape[0], 1))
>>> c = np.zeros((halfspaces.shape[1],))
>>> c[-1] = -1
>>> A = np.hstack((halfspaces[:, :-1], norm_vector))
>>> b = - halfspaces[:, -1:]
>>> res = linprog(c, A_ub=A, b_ub=b, bounds=(None, None))
>>> x = res.x[:-1]
>>> y = res.x[-1]
>>> circle = Circle(x, radius=y, alpha=0.3)
>>> ax.add_patch(circle)
>>> plt.legend(bbox_to_anchor=(1.6, 1.0))
>>> plt.show()

НазадОткрыть во вкладке