scipy.spatial.

SphericalVoronoi

класс scipy.spatial.SphericalVoronoi(точки, radius=1, центр=None, порог=1e-06)

Диаграммы Вороного на поверхности сферы.

Добавлено в версии 0.18.0.

Параметры:

точкиndarray из float, форма (npoints, ndim)

Координаты точек, из которых строится сферическая диаграмма Вороного.

radiusfloat, опционально

Радиус сферы (по умолчанию: 1)

центрndarray из float, форма (ndim,)

Центр сферы (по умолчанию: начало координат)

порогfloat

Порог для обнаружения дублирующихся точек и несоответствий между точками и параметрами сферы. (По умолчанию: 1e-06)

Атрибуты:

точкидвойной массив формы (npoints, ndim)

точки в ndim размерности для генерации диаграммы Вороного из

radiusdouble

радиус сферы

центрдвойной массив формы (ndim,)

центр сферы

вершиныдвумерный массив формы (nvertices, ndim)

Вершины Вороного, соответствующие точкам

областисписок списков целых чисел формы (npoints, _ )

n-я запись представляет собой список индексов вершин, принадлежащих n-й точке в points

Методы

calculate_areas()

Вычисляет площади регионов Вороного.

Вызывает:

ValueError

Если есть дубликаты в точки. Если предоставленный radius не согласуется с точки.

Смотрите также

Voronoi

Обычные диаграммы Вороного в N измерениях.

Примечания

Алгоритм сферической диаграммы Вороного работает следующим образом. Выпуклая оболочка входных точек (генераторов) вычисляется и эквивалентна их триангуляции Делоне на поверхности сферы [Caroli]. Информация о соседях выпуклой оболочки затем используется для упорядочивания вершин области Вороного вокруг каждого генератора. Последний подход существенно менее чувствителен к проблемам с плавающей точкой, чем методы сортировки вершин области Вороного на основе углов.

Эмпирическая оценка производительности алгоритма сферических диаграмм Вороного предполагает квадратичную временную сложность (логарифмически-линейная является оптимальной, но алгоритмы сложнее реализовать).

Ссылки

[Caroli]

Caroli et al. Robust and Efficient Delaunay triangulations of points on or close to a sphere. Research Report RR-7004, 2009.

[VanOosterom]

Ван Остером и Страки. Телесный угол плоского треугольника. IEEE Transactions on Biomedical Engineering, 2, 1983, стр. 125–126.

Примеры

Попробуйте в вашем браузере!

Выполнить некоторые импорты и взять некоторые точки на кубе:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.spatial import SphericalVoronoi, geometric_slerp
>>> from mpl_toolkits.mplot3d import proj3d
>>> # set input data
>>> points = np.array([[0, 0, 1], [0, 0, -1], [1, 0, 0],
...                    [0, 1, 0], [0, -1, 0], [-1, 0, 0], ])

Вычислить сферическую диаграмму Вороного:

>>> radius = 1
>>> center = np.array([0, 0, 0])
>>> sv = SphericalVoronoi(points, radius, center)

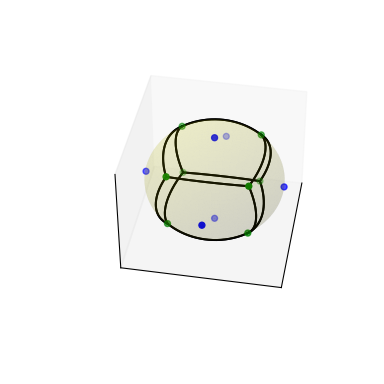
Сгенерировать график:

>>> # sort vertices (optional, helpful for plotting)
>>> sv.sort_vertices_of_regions()
>>> t_vals = np.linspace(0, 1, 2000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> # plot the unit sphere for reference (optional)
>>> u = np.linspace(0, 2 * np.pi, 100)
>>> v = np.linspace(0, np.pi, 100)
>>> x = np.outer(np.cos(u), np.sin(v))
>>> y = np.outer(np.sin(u), np.sin(v))
>>> z = np.outer(np.ones(np.size(u)), np.cos(v))
>>> ax.plot_surface(x, y, z, color='y', alpha=0.1)
>>> # plot generator points
>>> ax.scatter(points[:, 0], points[:, 1], points[:, 2], c='b')
>>> # plot Voronoi vertices
>>> ax.scatter(sv.vertices[:, 0], sv.vertices[:, 1], sv.vertices[:, 2],
...                    c='g')
>>> # indicate Voronoi regions (as Euclidean polygons)
>>> for region in sv.regions:
...    n = len(region)
...    for i in range(n):
...        start = sv.vertices[region][i]
...        end = sv.vertices[region][(i + 1) % n]
...        result = geometric_slerp(start, end, t_vals)
...        ax.plot(result[..., 0],
...                result[..., 1],
...                result[..., 2],
...                c='k')
>>> ax.azim = 10
>>> ax.elev = 40
>>> _ = ax.set_xticks([])
>>> _ = ax.set_yticks([])
>>> _ = ax.set_zticks([])
>>> fig.set_size_inches(4, 4)
>>> plt.show()

НазадОткрыть во вкладке