scipy.spatial.cKDTree.

query_ball_tree#

cKDTree.query_ball_tree(self, other, r, p=2., eps=0)#

Найти все пары точек между self и other расстояние до которого не превышает r

Параметры:

otherэкземпляр cKDTree: Дерево, содержащее точки для поиска.
rfloat: Максимальное расстояние, должно быть положительным.
pfloat, опционально: Какую норму Минковского использовать. p должно удовлетворять условию 1 <= p <= infinity. Конечное большое p может вызвать ValueError, если может произойти переполнение.
epsfloat, опционально: Приближённый поиск. Ветви дерева не исследуются, если их ближайшие точки находятся дальше, чем r/(1+eps), и ветви добавляются массово, если их самые дальние точки ближе, чем r * (1+eps). eps должно быть неотрицательным.

Возвращает:

FeatureHasher на частотных словаряхсписок списков: Для каждого элемента self.data[i] этого дерева, results[i] является списком индексов его соседей в other.data.

Примеры

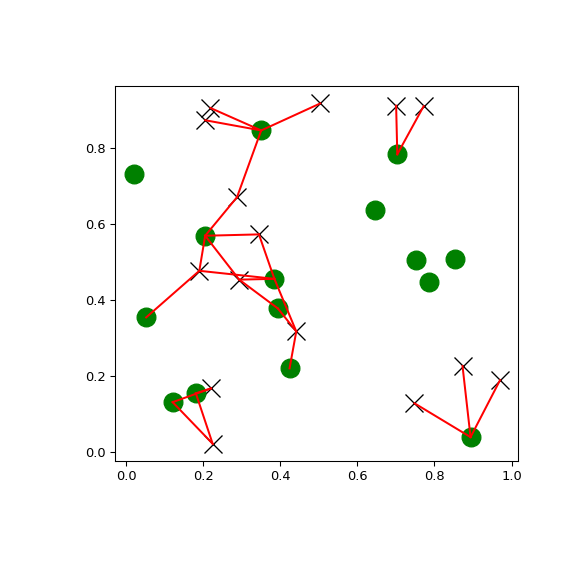
Вы можете искать все пары точек между двумя kd-деревьями в пределах расстояния:

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.spatial import cKDTree
>>> rng = np.random.default_rng()
>>> points1 = rng.random((15, 2))
>>> points2 = rng.random((15, 2))
>>> plt.figure(figsize=(6, 6))
>>> plt.plot(points1[:, 0], points1[:, 1], "xk", markersize=14)
>>> plt.plot(points2[:, 0], points2[:, 1], "og", markersize=14)
>>> kd_tree1 = cKDTree(points1)
>>> kd_tree2 = cKDTree(points2)
>>> indexes = kd_tree1.query_ball_tree(kd_tree2, r=0.2)
>>> for i in range(len(indexes)):
...     for j in indexes[i]:
...         plt.plot([points1[i, 0], points2[j, 0]],
...             [points1[i, 1], points2[j, 1]], "-r")
>>> plt.show()

../../_images/scipy-spatial-cKDTree-query_ball_tree-1.png