scipy.spatial.

geometric_slerp#

scipy.spatial.geometric_slerp(начало, end, t, tol=1e-07)[источник]#

Геометрическая сферическая линейная интерполяция.

Интерполяция происходит вдоль дуги большого круга единичного радиуса в пространстве произвольной размерности.

Параметры:
начало(n_dimensions, ) array-like

Одна n-мерная входная координата в объекте, подобном 1-D массиву. n должны быть больше 1.

end(n_dimensions, ) array-like

Одна n-мерная входная координата в объекте, подобном 1-D массиву. n должны быть больше 1.

tfloat или (n_points,) 1D array-like

Вещественное число или одномерный массивоподобный объект из чисел с плавающей точкой, представляющий параметры интерполяции, со значениями в замкнутом интервале от 0 до 1. Распространенный подход — сгенерировать массив с помощью np.linspace(0, 1, n_pts) для линейно распределенных точек. Допускаются возрастающий, убывающий и перемешанный порядок.

tolfloat

Абсолютный допуск для определения, являются ли начальные и конечные координаты антиподами.

Возвращает:
результат(t.size, D)

Массив двойной точности, содержащий интерполированный сферический путь и включающий начало и конец при использовании t=0 и t=1. Интерполированные значения должны соответствовать тому же порядку сортировки, указанному в массиве t. Результат может быть одномерным, если t является числом с плавающей точкой.

Вызывает:
ValueError

Если start и end являются антиподами, не на единичной n-сфере или для различных вырожденных условий.

Смотрите также

scipy.spatial.transform.Slerp

3-D Slerp, работающий с кватернионами

Примечания

Реализация основана на математической формуле, приведенной в [1], и первое известное представление этого алгоритма, выведенное из изучения 4-D геометрии, приписывается Glenn Davis в сноске оригинальной публикации quaternion Slerp от Ken Shoemake [2].

Добавлено в версии 1.5.0.

Ссылки

[2]

Ken Shoemake (1985) Анимация вращения с помощью кватернионных кривых. ACM SIGGRAPH Computer Graphics, 19(3): 245-254.

Примеры

Интерполяция четырех линейно-равномерных значений на окружности круга, охватывающей 90 градусов:

>>> import numpy as np
>>> from scipy.spatial import geometric_slerp
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> start = np.array([1, 0])
>>> end = np.array([0, 1])
>>> t_vals = np.linspace(0, 1, 4)
>>> result = geometric_slerp(start,
...                          end,
...                          t_vals)

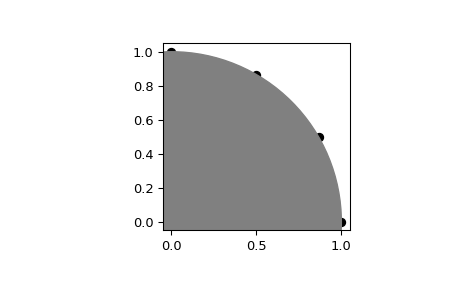
Интерполированные результаты должны быть с интервалами 30 градусов распознаваемыми на единичной окружности:

>>> ax.scatter(result[...,0], result[...,1], c='k')
>>> circle = plt.Circle((0, 0), 1, color='grey')
>>> ax.add_artist(circle)
>>> ax.set_aspect('equal')
>>> plt.show()
../../_images/scipy-spatial-geometric_slerp-1_00_00.png

Попытка интерполяции между антиподами на окружности неоднозначна, потому что есть два возможных пути, а на сфере есть бесконечное количество возможных путей на геодезической поверхности. Тем не менее, один из неоднозначных путей возвращается вместе с предупреждением:

>>> opposite_pole = np.array([-1, 0])
>>> with np.testing.suppress_warnings() as sup:
...     sup.filter(UserWarning)
...     geometric_slerp(start,
...                     opposite_pole,
...                     t_vals)
array([[ 1.00000000e+00,  0.00000000e+00],
       [ 5.00000000e-01,  8.66025404e-01],
       [-5.00000000e-01,  8.66025404e-01],
       [-1.00000000e+00,  1.22464680e-16]])

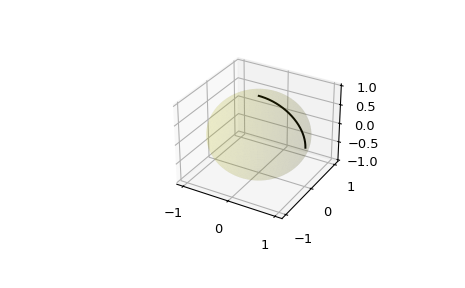
Расширьте исходный пример до сферы и постройте точки интерполяции в 3D:

>>> from mpl_toolkits.mplot3d import proj3d
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')

Постройте единичную сферу для справки (опционально):

>>> u = np.linspace(0, 2 * np.pi, 100)
>>> v = np.linspace(0, np.pi, 100)
>>> x = np.outer(np.cos(u), np.sin(v))
>>> y = np.outer(np.sin(u), np.sin(v))
>>> z = np.outer(np.ones(np.size(u)), np.cos(v))
>>> ax.plot_surface(x, y, z, color='y', alpha=0.1)

Интерполяция по большему количеству точек может создать видимость гладкой кривой на поверхности сферы, что также полезно для дискретизированных интегральных вычислений на поверхности сферы:

>>> start = np.array([1, 0, 0])
>>> end = np.array([0, 0, 1])
>>> t_vals = np.linspace(0, 1, 200)
>>> result = geometric_slerp(start,
...                          end,
...                          t_vals)
>>> ax.plot(result[...,0],
...         result[...,1],
...         result[...,2],
...         c='k')
>>> plt.show()
../../_images/scipy-spatial-geometric_slerp-1_01_00.png
На этой странице