scipy.special.

y0_zeros#

scipy.special.y0_zeros(nt, комплексный=False)[источник]#

Вычислить nt нулей функции Бесселя Y0(z) и производную в каждом нуле.

Производные задаются как Y0’(z0) = -Y1(z0) в каждом нуле z0.

Параметры:

ntint: Количество нулей для возврата
комплексныйbool, по умолчанию False: Установите False, чтобы возвращать только действительные нули; установите True, чтобы возвращать только комплексные нули с отрицательной действительной частью и положительной мнимой частью. Обратите внимание, что комплексно-сопряженные к последним также являются нулями функции, но не возвращаются этой процедурой.

Возвращает:

z0nndarray: Расположение n-го нуля Y0(z)
y0pz0nndarray: Значение производной Y0’(z0) для n-го нуля

Ссылки

[1]

Zhang, Shanjie and Jin, Jianming. “Computation of Special Functions”, John Wiley and Sons, 1996, chapter 5. https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

Примеры

Вычислить первые 4 вещественных корня и производные в корнях \(Y_0\):

>>> import numpy as np
>>> from scipy.special import y0_zeros
>>> zeros, grads = y0_zeros(4)
>>> with np.printoptions(precision=5):
...     print(f"Roots: {zeros}")
...     print(f"Gradients: {grads}")
Roots: [ 0.89358+0.j  3.95768+0.j  7.08605+0.j 10.22235+0.j]
Gradients: [-0.87942+0.j  0.40254+0.j -0.3001 +0.j  0.2497 +0.j]

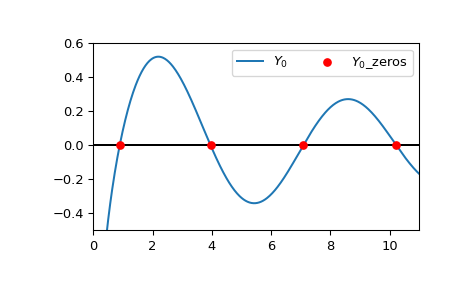
Построить действительную часть \(Y_0\) и первые четыре вычисленных корня.

>>> import matplotlib.pyplot as plt
>>> from scipy.special import y0
>>> xmin = 0
>>> xmax = 11
>>> x = np.linspace(xmin, xmax, 500)
>>> fig, ax = plt.subplots()
>>> ax.hlines(0, xmin, xmax, color='k')
>>> ax.plot(x, y0(x), label=r'$Y_0$')
>>> zeros, grads = y0_zeros(4)
>>> ax.scatter(zeros.real, np.zeros((4, )), s=30, c='r',
...            label=r'$Y_0$_zeros', zorder=5)
>>> ax.set_ylim(-0.5, 0.6)
>>> ax.set_xlim(xmin, xmax)
>>> plt.legend(ncol=2)
>>> plt.show()

../../_images/scipy-special-y0_zeros-1_00_00.png

Вычислить первые 4 комплексных корня и производные в корнях \(Y_0\) установкой complex=True:

>>> y0_zeros(4, True)
(array([ -2.40301663+0.53988231j,  -5.5198767 +0.54718001j,
         -8.6536724 +0.54841207j, -11.79151203+0.54881912j]),
 array([ 0.10074769-0.88196771j, -0.02924642+0.5871695j ,
         0.01490806-0.46945875j, -0.00937368+0.40230454j]))