scipy.stats.

Смесь#

класс scipy.stats.Смесь(компоненты, *, веса=None)[источник]#

Представление смешанного распределения.

Смешанное распределение — это распределение случайной величины, определенной следующим образом: сначала выбирается случайная величина из components в соответствии с вероятностями, заданными weights, затем выбранная случайная величина реализуется.

Параметры:

компонентыпоследовательность ContinuousDistribution: Базовые экземпляры ContinuousDistribution. Все должны иметь скалярные параметры формы (если есть); например, pdf вычисленная при скалярном аргументе должна возвращать скаляр.
весапоследовательность чисел с плавающей точкой, опционально: Соответствующие вероятности выбора каждой случайной величины. Должны быть неотрицательными и в сумме давать единицу. Поведение по умолчанию — взвешивать все компоненты одинаково.

Атрибуты:

компонентыпоследовательность ContinuousDistribution: Базовые экземпляры ContinuousDistribution.
весаndarray: Соответствующие вероятности выбора каждой случайной величины.

Методы

`support`()	Носитель случайной величины
`sample`([shape, rng, method])	Случайная выборка из распределения.
`moment`([order, kind, method])	Сырой, центральный или стандартный момент положительного целого порядка.
`mean`(*[, method])	Среднее (сырой первый момент относительно начала координат)
`median`(*[, method])	Медиана (50-й процентиль)
`mode`(*[, method])	Мода (наиболее вероятное значение)
`variance`(*[, method])	Дисперсия (центральный момент второго порядка)
`standard_deviation`(*[, method])	Стандартное отклонение (квадратный корень из второго центрального момента)
`skewness`(*[, method])	Асимметрия (стандартизированный третий момент)
`kurtosis`(*[, method])	Эксцесс (стандартизированный четвертый момент)
`pdf`(x, /, *[, method])	Функция плотности вероятности
`logpdf`(x, /, *[, method])	Логарифм функции плотности вероятности
`cdf`(x[, y, method])	Функция кумулятивного распределения
`icdf`(p, /, *[, method])	Обратная функция распределения.
`ccdf`(x[, y, method])	Дополнительная функция распределения
`iccdf`(p, /, *[, method])	Обратная дополнительная кумулятивная функция распределения.
`logcdf`(x[, y, method])	Логарифм функции кумулятивного распределения
`ilogcdf`(p, /, *[, method])	Обратная функция логарифма кумулятивной функции распределения.
`logccdf`(x[, y, method])	Логарифм дополнительной кумулятивной функции распределения
`ilogccdf`(p, /, *[, method])	Обратная функция логарифма дополнительной функции распределения.
`entropy`(*[, method])	Дифференциальная энтропия

Примечания

В документации используются следующие сокращения.

PDF: функция плотности вероятности
CDF: функция распределения
CCDF: дополнительная функция распределения
энтропия: дифференциальная энтропия
log-F: логарифм F (например, log-CDF)
обратный F: обратная функция к F (например, обратная функция распределения)

Ссылки

[1]

Смешанное распределение, Википедия, https://en.wikipedia.org/wiki/Mixture_distribution

Примеры

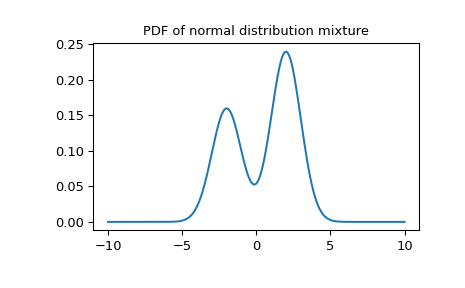
Смесь нормальных распределений:

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> X1 = stats.Normal(mu=-2, sigma=1)
>>> X2 = stats.Normal(mu=2, sigma=1)
>>> mixture = stats.Mixture([X1, X2], weights=[0.4, 0.6])
>>> print(f'mean: {mixture.mean():.2f}, '
...       f'median: {mixture.median():.2f}, '
...       f'mode: {mixture.mode():.2f}')
mean: 0.40, median: 1.04, mode: 2.00
>>> x = np.linspace(-10, 10, 300)
>>> plt.plot(x, mixture.pdf(x))
>>> plt.title('PDF of normal distribution mixture')
>>> plt.show()