scipy.stats.Uniform.

plot

Равномерное.plot(x='x', y=None, *, t=None, ax=None)

Построить график функции распределения.

Удобная функция для быстрой визуализации распределения, лежащего в основе случайной величины.

Параметры:

x, ystr, optional

Строка, указывающая величины, используемые в качестве абсциссы и ординаты (горизонтальной и вертикальной координат) соответственно. Значения по умолчанию: 'x' (область определения случайной величины) и либо 'pdf' (функция плотности вероятности) (непрерывная) или 'pdf' (функция плотности вероятности) (дискретная). Допустимые значения: 'x', 'pdf', 'pmf', 'cdf', 'ccdf', 'icdf', 'iccdf', 'logpdf', 'logpmf', 'logcdf', 'logccdf', 'ilogcdf', 'ilogccdf'.

t3-кортеж (str, float, float), опционально

Кортеж, указывающий пределы, в пределах которых отображаются величины. По умолчанию ('cdf', 0.0005, 0.9995) если область бесконечна, указывая, что центральные 99.9% распределения должны быть показаны; иначе используются конечные точки носителя, где они конечны. Допустимые значения: ‘x’, ‘cdf’, ‘ccdf’, ‘icdf’, ‘iccdf’, ‘logcdf’, ‘logccdf’, ‘ilogcdf’, ‘ilogccdf’.

axmatplotlib.axes, опционально

Оси, на которых строить график. Если не указаны, используются текущие оси.

Возвращает:

axmatplotlib.axes

Оси, на которых был построен график. График можно настроить, манипулируя этим объектом.

Примеры

Попробуйте в вашем браузере!

любым из целых чисел в полуоткрытом диапазоне

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> X = stats.Normal(mu=1., sigma=2.)

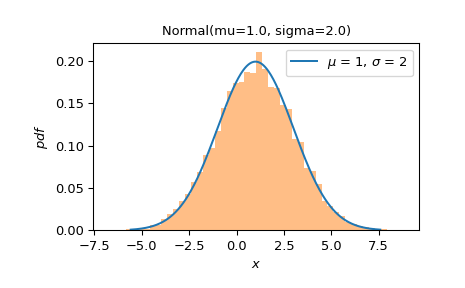
Постройте PDF в центральных 99.9% распределения. Сравните с гистограммой случайной выборки.

>>> ax = X.plot()
>>> sample = X.sample(10000)
>>> ax.hist(sample, density=True, bins=50, alpha=0.5)
>>> plt.show()

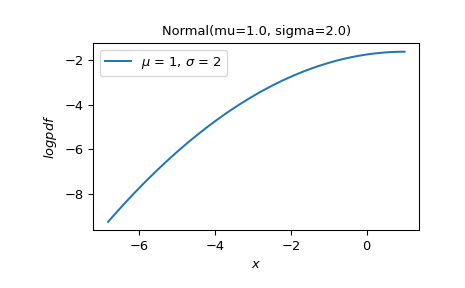
Построить график logpdf(x) как функция от x в левом хвосте, где логарифм CDF находится между -10 и np.log(0.5).

>>> X.plot('x', 'logpdf', t=('logcdf', -10, np.log(0.5)))
>>> plt.show()

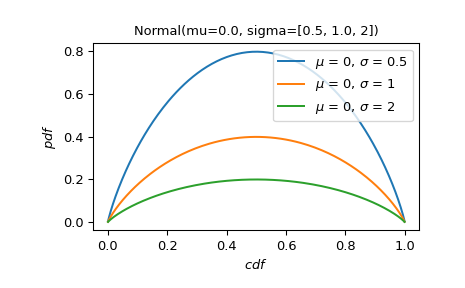
Построить график PDF нормального распределения как функции CDF для различных значений параметра масштаба.

>>> X = stats.Normal(mu=0., sigma=[0.5, 1., 2])
>>> X.plot('cdf', 'pdf')
>>> plt.show()

НазадОткрыть во вкладке