scipy.stats.

bayes_mvs

scipy.stats.bayes_mvs(данные, alpha=0.9)

Байесовские доверительные интервалы для среднего, дисперсии и стандартного отклонения.

Параметры:

данныеarray_like

Входные данные, если многомерные, преобразуются в 1-D путем bayes_mvs. Требуется 2 или более точек данных.

alphafloat, опционально

Вероятность того, что возвращенный доверительный интервал содержит истинный параметр.

Возвращает:

mean_cntr, var_cntr, std_cntrкортеж

Три результата соответствуют среднему значению, дисперсии и стандартному отклонению соответственно. Каждый результат представляет собой кортеж вида:

(center, (lower, upper))

с center среднее условной плотности вероятности значения при заданных данных, и (lower, upper) доверительный интервал, центрированный на медиане, содержащий оценку с вероятностью alpha.

Смотрите также

mvsdist

Примечания

Каждый кортеж оценок среднего, дисперсии и стандартного отклонения представляет (центр, (нижняя, верхняя)), где центр — среднее условной плотности вероятности значения при данных, а (нижняя, верхняя) — доверительный интервал, центрированный на медиане, содержащий оценку с вероятностью alpha.

Преобразует данные в 1-D и предполагает, что все данные имеют одинаковое среднее значение и дисперсию. Использует априорное распределение Джеффриса для дисперсии и стандартного отклонения.

Эквивалентно tuple((x.mean(), x.interval(alpha)) for x in mvsdist(dat))

Ссылки

T.E. Oliphant, «Байесовский взгляд на оценку среднего, дисперсии и стандартного отклонения по данным», https://scholarsarchive.byu.edu/facpub/278, 2006.

Примеры

Попробуйте в вашем браузере!

Сначала базовый пример для демонстрации результатов:

>>> from scipy import stats
>>> data = [6, 9, 12, 7, 8, 8, 13]
>>> mean, var, std = stats.bayes_mvs(data)
>>> mean
Mean(statistic=9.0, minmax=(7.103650222612533, 10.896349777387467))
>>> var
Variance(statistic=10.0, minmax=(3.176724206, 24.45910382))
>>> std
Std_dev(statistic=2.9724954732045084,
        minmax=(1.7823367265645143, 4.945614605014631))

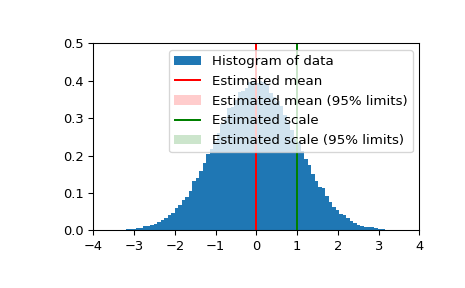
Теперь мы генерируем некоторые случайные данные с нормальным распределением и получаем оценки среднего и стандартного отклонения с 95% доверительными интервалами для этих оценок:

>>> n_samples = 100000
>>> data = stats.norm.rvs(size=n_samples)
>>> res_mean, res_var, res_std = stats.bayes_mvs(data, alpha=0.95)

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.hist(data, bins=100, density=True, label='Histogram of data')
>>> ax.vlines(res_mean.statistic, 0, 0.5, colors='r', label='Estimated mean')
>>> ax.axvspan(res_mean.minmax[0],res_mean.minmax[1], facecolor='r',
...            alpha=0.2, label=r'Estimated mean (95% limits)')
>>> ax.vlines(res_std.statistic, 0, 0.5, colors='g', label='Estimated scale')
>>> ax.axvspan(res_std.minmax[0],res_std.minmax[1], facecolor='g', alpha=0.2,
...            label=r'Estimated scale (95% limits)')

>>> ax.legend(fontsize=10)
>>> ax.set_xlim([-4, 4])
>>> ax.set_ylim([0, 0.5])
>>> plt.show()

НазадОткрыть во вкладке