binned_statistic#
- scipy.stats.binned_statistic(x, values, статистика='mean', bins=10, range=None)[источник]#
Вычислить бинированную статистику для одного или нескольких наборов данных.
Это обобщение функции гистограммы. Гистограмма делит пространство на бины и возвращает количество точек в каждом бине. Эта функция позволяет вычислять сумму, среднее, медиану или другую статистику значений (или набора значений) в каждом бине.
- Параметры:
- x(N,) array_like
Последовательность значений для бинирования.
- values(N,) array_like или список из (N,) array_like
Данные, по которым будет вычисляться статистика. Они должны иметь ту же форму, что и x, или набор последовательностей - каждая той же формы, что и x. Если values является набором последовательностей, статистика будет вычислена для каждой независимо.
- статистикастрока или вызываемый объект, необязательный
Статистика для вычисления (по умолчанию 'mean'). Доступны следующие статистики:
‘mean’ : вычисляет среднее значений точек в каждом бине. Пустые бины будут представлены NaN.
'std' : вычисляет стандартное отклонение внутри каждого бина. Это неявно рассчитывается с ddof=0.
‘median’ : вычисляет медиану значений для точек в каждом бине. Пустые бины будут представлены NaN.
'count' : вычисление количества точек в каждом бине. Это идентично невзвешенной гистограмме. values массив не используется.
‘sum’ : вычисляет сумму значений для точек в каждом бине. Это идентично взвешенной гистограмме.
'min' : вычисляет минимальное значение точек в каждом бине. Пустые бины будут представлены NaN.
‘max’ : вычисление максимального значения для точек в каждом бине. Пустые бины будут представлены NaN.
функция : пользовательская функция, которая принимает 1D массив значений и выводит одну числовую статистику. Эта функция будет вызываться для значений в каждом бине. Пустые бины будут представлены как function([]) или NaN, если это возвращает ошибку.
- binsint или последовательность скаляров, опционально
Если bins является целым числом, он определяет количество равных по ширине бинов в заданном диапазоне (10 по умолчанию). Если bins является последовательностью, она определяет границы бинов, включая правую границу, позволяя использовать неравномерную ширину бинов. Значения в x которые меньше нижнего края бина, присваиваются номеру бина 0, значения выше самого высокого бина присваиваются
bins[-1]. Если границы бинов указаны, количество бинов будет (nx = len(bins)-1).- range(float, float) или [(float, float)], опционально
Нижний и верхний диапазоны бинов. Если не указаны, диапазон просто
(x.min(), x.max()). Значения вне диапазона игнорируются.
- Возвращает:
- статистикамассив
Значения выбранной статистики в каждом бине.
- bin_edgesмассив типа float
Возвращает границы бинов
(length(statistic)+1).- binnumber: одномерный массив ndarray целых чисел
Индексы бинов (соответствующие bin_edges) в котором каждое значение x принадлежит. Та же длина, что и values. Номер бина i означает, что соответствующее значение находится между (bin_edges[i-1], bin_edges[i]).
Смотрите также
Примечания
Все, кроме последнего (самого правого) интервала, полуоткрыты. Другими словами, если bins является
[1, 2, 3, 4], тогда первый бинарный интервал[1, 2)(включая 1, но исключая 2) и второй[2, 3). Однако последний бинар[3, 4], который includes 4.Добавлено в версии 0.11.0.
Примеры
>>> import numpy as np >>> from scipy import stats >>> import matplotlib.pyplot as plt
Сначала несколько базовых примеров:
Создайте два равномерно распределённых бина в диапазоне заданной выборки и просуммируйте соответствующие значения в каждом из этих бинов:
>>> values = [1.0, 1.0, 2.0, 1.5, 3.0] >>> stats.binned_statistic([1, 1, 2, 5, 7], values, 'sum', bins=2) BinnedStatisticResult(statistic=array([4. , 4.5]), bin_edges=array([1., 4., 7.]), binnumber=array([1, 1, 1, 2, 2]))
Также можно передать несколько массивов значений. Статистика вычисляется для каждого набора независимо:
>>> values = [[1.0, 1.0, 2.0, 1.5, 3.0], [2.0, 2.0, 4.0, 3.0, 6.0]] >>> stats.binned_statistic([1, 1, 2, 5, 7], values, 'sum', bins=2) BinnedStatisticResult(statistic=array([[4. , 4.5], [8. , 9. ]]), bin_edges=array([1., 4., 7.]), binnumber=array([1, 1, 1, 2, 2]))
>>> stats.binned_statistic([1, 2, 1, 2, 4], np.arange(5), statistic='mean', ... bins=3) BinnedStatisticResult(statistic=array([1., 2., 4.]), bin_edges=array([1., 2., 3., 4.]), binnumber=array([1, 2, 1, 2, 3]))
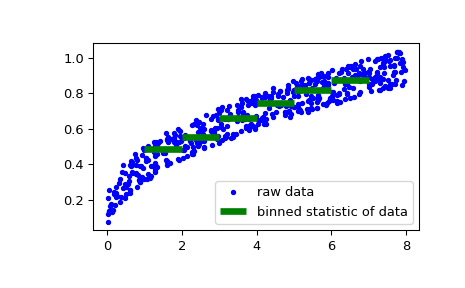
В качестве второго примера мы генерируем случайные данные о скорости парусной лодки в зависимости от скорости ветра, а затем определяем, насколько быстра наша лодка при определенных скоростях ветра:
>>> rng = np.random.default_rng() >>> windspeed = 8 * rng.random(500) >>> boatspeed = .3 * windspeed**.5 + .2 * rng.random(500) >>> bin_means, bin_edges, binnumber = stats.binned_statistic(windspeed, ... boatspeed, statistic='median', bins=[1,2,3,4,5,6,7]) >>> plt.figure() >>> plt.plot(windspeed, boatspeed, 'b.', label='raw data') >>> plt.hlines(bin_means, bin_edges[:-1], bin_edges[1:], colors='g', lw=5, ... label='binned statistic of data') >>> plt.legend()
Теперь мы можем использовать
binnumberчтобы выбрать все точки данных со скоростью ветра ниже 1:>>> low_boatspeed = boatspeed[binnumber == 0]
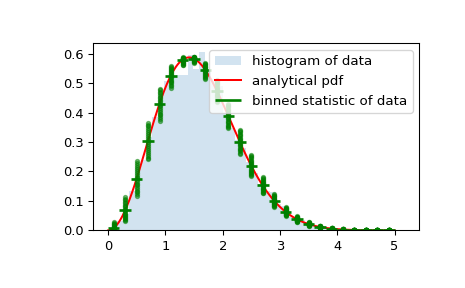
В качестве последнего примера мы используем
bin_edgesиbinnumberчтобы построить график распределения, показывающий среднее значение и распределение вокруг этого среднего по бинам, поверх обычной гистограммы и функции плотности вероятности:>>> x = np.linspace(0, 5, num=500) >>> x_pdf = stats.maxwell.pdf(x) >>> samples = stats.maxwell.rvs(size=10000)
>>> bin_means, bin_edges, binnumber = stats.binned_statistic(x, x_pdf, ... statistic='mean', bins=25) >>> bin_width = (bin_edges[1] - bin_edges[0]) >>> bin_centers = bin_edges[1:] - bin_width/2
>>> plt.figure() >>> plt.hist(samples, bins=50, density=True, histtype='stepfilled', ... alpha=0.2, label='histogram of data') >>> plt.plot(x, x_pdf, 'r-', label='analytical pdf') >>> plt.hlines(bin_means, bin_edges[:-1], bin_edges[1:], colors='g', lw=2, ... label='binned statistic of data') >>> plt.plot((binnumber - 0.5) * bin_width, x_pdf, 'g.', alpha=0.5) >>> plt.legend(fontsize=10) >>> plt.show()