scipy.stats.

circvar#

scipy.stats.circvar(образцы, высокий=6.283185307179586, низкий=0, ось=None, nan_policy='propagate', *, keepdims=False)[источник]#

Вычислить круговую дисперсию выборки угловых наблюдений.

Учитывая \(n\) угловые наблюдения \(x_1, \cdots, x_n\) измеряется в радианах, их круговая дисперсия определяется как ([2], Ур. 2.3.3)

\[1 - \left| \frac{1}{n} \sum_{k=1}^n e^{i x_k} \right|\]

где \(i\) является мнимой единицей, а \(|z|\) даёт длину комплексного числа \(z\). \(|z|\) в приведенном выше выражении известно как средняя результирующая длина.

Параметры:

образцыarray_like

Входной массив наблюдений углов. Значение полного угла равно (high - low).

высокийfloat, опционально

Верхняя граница главного значения угла. По умолчанию 2*pi.

низкийfloat, опционально

Нижняя граница главного значения угла. По умолчанию 0.

осьint или None, по умолчанию: None

Если это целое число, ось входных данных, по которой вычисляется статистика. Статистика каждого среза по оси (например, строки) входных данных появится в соответствующем элементе вывода. Если None, вход будет сведён в одномерный массив перед вычислением статистики.

nan_policy{‘propagate’, ‘omit’, ‘raise’}

Определяет, как обрабатывать входные значения NaN.

propagate: если NaN присутствует в срезе оси (например, строке), вдоль которой вычисляется статистика, соответствующая запись вывода будет NaN.
omit: NaN будут пропущены при выполнении расчета. Если в срезе оси, вдоль которого вычисляется статистика, остается недостаточно данных, соответствующая запись вывода будет NaN.
raise: если присутствует NaN, то ValueError будет вызвано исключение.

keepdimsbool, по умолчанию: False

Если установлено значение True, оси, которые были сокращены, остаются в результате как размерности с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.

Возвращает:

circvarfloat

Круговая дисперсия. Возвращаемое значение находится в диапазоне [0, 1], где 0 указывает на отсутствие дисперсии и 1 указывает на большую дисперсию.

Если входной массив пуст, np.nan возвращается.

Смотрите также

circmean: Круговая средняя.
circstd: Круговое стандартное отклонение.

Примечания

В пределе малых углов круговая дисперсия близка к половине 'линейной' дисперсии, если измеряется в радианах.

Начиная с SciPy 1.9, np.matrix входные данные (не рекомендуется для нового кода) преобразуются в np.ndarray перед выполнением вычисления. В этом случае результатом будет скаляр или np.ndarray подходящей формы вместо 2D np.matrix. Аналогично, хотя маскированные элементы маскированных массивов игнорируются, результатом будет скаляр или np.ndarray вместо маскированного массива с mask=False.

Ссылки

[1]

Фишер, Н.И. Статистический анализ циклических данных. Cambridge University Press, 1993.

[2]

Мардия, К. В. и Джапп, П. Е. Направленная статистика. John Wiley & Sons, 1999.

Примеры

>>> import numpy as np
>>> from scipy.stats import circvar
>>> import matplotlib.pyplot as plt
>>> samples_1 = np.array([0.072, -0.158, 0.077, 0.108, 0.286,
...                       0.133, -0.473, -0.001, -0.348, 0.131])
>>> samples_2 = np.array([0.111, -0.879, 0.078, 0.733, 0.421,
...                       0.104, -0.136, -0.867,  0.012,  0.105])
>>> circvar_1 = circvar(samples_1)
>>> circvar_2 = circvar(samples_2)

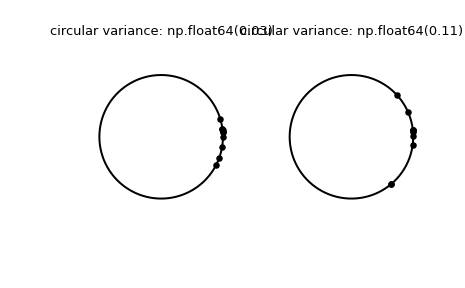
Постройте график выборок.

>>> fig, (left, right) = plt.subplots(ncols=2)
>>> for image in (left, right):
...     image.plot(np.cos(np.linspace(0, 2*np.pi, 500)),
...                np.sin(np.linspace(0, 2*np.pi, 500)),
...                c='k')
...     image.axis('equal')
...     image.axis('off')
>>> left.scatter(np.cos(samples_1), np.sin(samples_1), c='k', s=15)
>>> left.set_title(f"circular variance: {np.round(circvar_1, 2)!r}")
>>> right.scatter(np.cos(samples_2), np.sin(samples_2), c='k', s=15)
>>> right.set_title(f"circular variance: {np.round(circvar_2, 2)!r}")
>>> plt.show()