scipy.stats.

differential_entropy

scipy.stats.differential_entropy(values, *, window_length=None, основание=None, ось=0, метод='auto', nan_policy='propagate', keepdims=False)

По выборке из распределения оценить дифференциальную энтропию.

Доступно несколько методов оценки с использованием метод параметр. По умолчанию метод выбирается на основе размера выборки.

Параметры:

valuesпоследовательность

Выборка из непрерывного распределения.

window_lengthint, необязательный

Длина окна для вычисления оценки Васичека. Должна быть целым числом между 1 и половиной размера выборки. Если None (по умолчанию), он использует эвристическое значение

\[\left \lfloor \sqrt{n} + 0.5 \right \rfloor\]

где \(n\) — это размер выборки. Эта эвристика была первоначально предложена в [2] и стал распространенным в литературе.

основаниеfloat, опционально

Логарифмическое основание для использования, по умолчанию e (натуральный логарифм).

осьint или None, по умолчанию: 0

Если это целое число, ось входных данных, по которой вычисляется статистика. Статистика каждого среза по оси (например, строки) входных данных появится в соответствующем элементе вывода. Если None, вход будет сведён в одномерный массив перед вычислением статистики.

метод{'vasicek', 'van es', 'ebrahimi', 'correa', 'auto'}, опционально

Метод, используемый для оценки дифференциальной энтропии из выборки. По умолчанию 'auto'. См. примечания для дополнительной информации.

nan_policy{‘propagate’, ‘omit’, ‘raise’}

Определяет, как обрабатывать входные значения NaN.

• propagate: если NaN присутствует в срезе оси (например, строке), вдоль которой вычисляется статистика, соответствующая запись вывода будет NaN.

• omit: NaN будут пропущены при выполнении расчета. Если в срезе оси, вдоль которого вычисляется статистика, остается недостаточно данных, соответствующая запись вывода будет NaN.

• raise: если присутствует NaN, то ValueError будет вызвано исключение.

keepdimsbool, по умолчанию: False

Если установлено значение True, оси, которые были сокращены, остаются в результате как размерности с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.

Возвращает:

энтропияfloat

Рассчитанная дифференциальная энтропия.

Примечания

Эта функция будет сходиться к истинной дифференциальной энтропии в пределе

\[n \to \infty, \quad m \to \infty, \quad \frac{m}{n} \to 0\]

Оптимальный выбор window_length для заданного размера выборки зависит от (неизвестного) распределения. Как правило, чем более гладкой является плотность распределения, тем больше оптимальное значение window_length [1].

Следующие опции доступны для метод параметр.

• 'vasicek' использует оценщик, представленный в [1]. Это один из первых и наиболее влиятельных оценщиков дифференциальной энтропии.

• 'van es' использует скорректированный на смещение оценщик, представленный в [3], который не только согласован, но и, при некоторых условиях, асимптотически нормален.

• 'ebrahimi' использует оценку, представленную в [4], который, как показано в моделировании, имеет меньшее смещение и среднеквадратичную ошибку, чем оценщик Васичека.

• 'correa' использует оценщик, представленный в [5] основанный на локальной линейной регрессии. В симуляционном исследовании он показал последовательно меньшую среднеквадратичную ошибку, чем оценщик Васичека, но его вычисление более затратно.

• 'auto' автоматически выбирает метод (по умолчанию). В настоящее время выбирается 'van es' для очень маленьких выборок (<10), 'ebrahimi' для умеренных размеров выборки (11-1000), и 'vasicek' для больших выборок, но это поведение может измениться в будущих версиях.

Все оценки реализованы, как описано в [6].

Начиная с SciPy 1.9, np.matrix входные данные (не рекомендуется для нового кода) преобразуются в np.ndarray перед выполнением вычисления. В этом случае результатом будет скаляр или np.ndarray подходящей формы вместо 2D np.matrix. Аналогично, хотя маскированные элементы маскированных массивов игнорируются, результатом будет скаляр или np.ndarray вместо маскированного массива с mask=False.

Ссылки

[1] (1,2)

Васичек, О. (1976). Тест на нормальность, основанный на выборочной энтропии. Журнал Королевского статистического общества: Серия B (Методологическая), 38(1), 54-59.

[2]

Crzcgorzewski, P., & Wirczorkowski, R. (1999). Entropy-based goodness-of-fit test for exponentiality. Communications in Statistics-Theory and Methods, 28(5), 1183-1202.

[3]

Van Es, B. (1992). Estimating functionals related to a density by a class of statistics based on spacings. Scandinavian Journal of Statistics, 61-72.

[4]

Ebrahimi, N., Pflughoeft, K., & Soofi, E. S. (1994). Two measures of sample entropy. Statistics & Probability Letters, 20(3), 225-234.

[5]

Correa, J. C. (1995). A new estimator of entropy. Communications in Statistics-Theory and Methods, 24(10), 2439-2449.

[6]

Noughabi, H. A. (2015). Entropy Estimation Using Numerical Methods. Annals of Data Science, 2(2), 231-241. https://link.springer.com/article/10.1007/s40745-015-0045-9

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> from scipy.stats import differential_entropy, norm

Энтропия стандартного нормального распределения:

>>> rng = np.random.default_rng()
>>> values = rng.standard_normal(100)
>>> differential_entropy(values)
1.3407817436640392

Сравните с истинной энтропией:

>>> float(norm.entropy())
1.4189385332046727

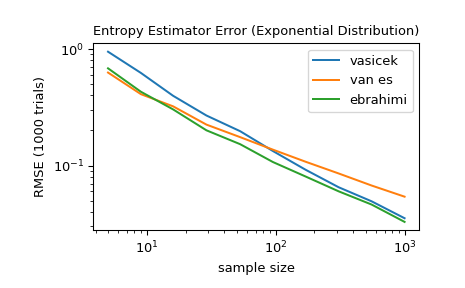
Для нескольких размеров выборки от 5 до 1000 сравните точность 'vasicek', 'van es', и 'ebrahimi' методов. В частности, сравните среднеквадратичную ошибку (по 1000 испытаний) между оценкой и истинной дифференциальной энтропией распределения.

>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>>
>>>
>>> def rmse(res, expected):
...     '''Root mean squared error'''
...     return np.sqrt(np.mean((res - expected)**2))
>>>
>>>
>>> a, b = np.log10(5), np.log10(1000)
>>> ns = np.round(np.logspace(a, b, 10)).astype(int)
>>> reps = 1000  # number of repetitions for each sample size
>>> expected = stats.expon.entropy()
>>>
>>> method_errors = {'vasicek': [], 'van es': [], 'ebrahimi': []}
>>> for method in method_errors:
...     for n in ns:
...        rvs = stats.expon.rvs(size=(reps, n), random_state=rng)
...        res = stats.differential_entropy(rvs, method=method, axis=-1)
...        error = rmse(res, expected)
...        method_errors[method].append(error)
>>>
>>> for method, errors in method_errors.items():
...     plt.loglog(ns, errors, label=method)
>>>
>>> plt.legend()
>>> plt.xlabel('sample size')
>>> plt.ylabel('RMSE (1000 trials)')
>>> plt.title('Entropy Estimator Error (Exponential Distribution)')

НазадОткрыть во вкладке