scipy.stats.

gaussian_kde

класс scipy.stats.gaussian_kde(набор данных, bw_method=None, веса=None)

Представление оценки плотности ядра с использованием гауссовских ядер.

Оценка плотности ядра — это способ оценки функции плотности вероятности (PDF) случайной величины непараметрическим методом. gaussian_kde работает как с одномерными, так и с многомерными данными. Он включает автоматическое определение ширины полосы. Оценка лучше всего работает для унимодального распределения; бимодальные или мультимодальные распределения имеют тенденцию к излишнему сглаживанию.

Параметры:

набор данныхarray_like

Точки данных для оценки. В случае одномерных данных это одномерный массив, в противном случае двумерный массив с формой (количество измерений, количество данных).

bw_methodstr, scalar or callable, optional

Метод, используемый для вычисления коэффициента ширины полосы. Это может быть ‘scott’, ‘silverman’, скалярная константа или вызываемый объект. Если скаляр, он будет использоваться напрямую как фактор. Если вызываемый объект, он должен принимать gaussian_kde экземпляр в качестве единственного параметра и возвращает скаляр. Если None (по умолчанию), используется ‘scott’. См. примечания для подробностей.

весаarray_like, необязательный

веса точек данных. Должны иметь ту же форму, что и набор данных. Если None (по умолчанию), предполагается, что выборки имеют одинаковый вес

Атрибуты:

набор данныхndarray

Набор данных, с которым gaussian_kde был инициализирован.

dint

Количество измерений.

nint

Количество точек данных.

neffint

Эффективное количество точек данных.

Добавлено в версии 1.2.0.

факторfloat

Полученный коэффициент полосы пропускания из covariance_factor.

ковариацияndarray

Матрица ковариации ядра; это матрица ковариации данных, умноженная на квадрат коэффициента полосы пропускания, например, np.cov(dataset) * factor**2.

inv_covndarray

Обратная величина ковариация.

Методы

evaluate(точки)	Оценить оценённую плотность вероятности на наборе точек.
__call__(точки)	Оценить оценённую плотность вероятности на наборе точек.
integrate_gaussian(mean, cov)	Умножить оцененную плотность на многомерное гауссово распределение и проинтегрировать по всему пространству.
integrate_box_1d(low, high)	Вычисляет интеграл одномерной функции плотности вероятности между двумя границами.
integrate_box(low_bounds, high_bounds[, ...])	Вычисляет интеграл функции плотности вероятности по прямоугольному интервалу.
integrate_kde(other)	Вычисляет интеграл произведения этой оценки плотности ядра с другой.
pdf(x)	Вычислить оценку плотности вероятности на предоставленном наборе точек.
logpdf(x)	Вычислить логарифм оценённой плотности вероятности на предоставленном наборе точек.
resample([size, seed])	Случайно выбрать набор данных из оценённой функции плотности вероятности.
set_bandwidth([bw_method])	Вычислить коэффициент полосы пропускания заданным методом.
covariance_factor()	Вычисляет коэффициент полосы пропускания фактор.

Примечания

Выбор ширины окна сильно влияет на оценку, полученную с помощью KDE (гораздо больше, чем фактическая форма ядра). Выбор ширины окна может осуществляться по «правилу большого пальца», с помощью перекрёстной проверки, «подстановочными методами» или другими способами; см. [3], [4] для обзоров. gaussian_kde использует эмпирическое правило, по умолчанию — правило Скотта.

Правило Скотта [1], реализовано как scotts_factor, это:

n**(-1./(d+4)),

с n количество точек данных и d количество измерений. В случае неравномерно взвешенных точек, scotts_factor становится:

neff**(-1./(d+4)),

с neff эффективного количества точек данных. Предложение Сильвермана для многомерный данные [2], реализовано как silverman_factor, это:

(n * (d + 2) / 4.)**(-1. / (d + 4)).

или в случае неравномерно взвешенных точек:

(neff * (d + 2) / 4.)**(-1. / (d + 4)).

Обратите внимание, что это не то же самое, что «правило большого пальца Сильвермана» [6], что может быть более устойчивым в одномерном случае; см. документацию set_bandwidth метод для реализации пользовательского правила ширины полосы.

Хорошие общие описания оценки плотности ядра можно найти в [1] и [2], математика для этой многомерной реализации может быть найдена в [1].

С набором взвешенных выборок, эффективное количество точек данных neff определяется как:

neff = sum(weights)^2 / sum(weights^2)

как подробно описано в [5].

gaussian_kde в настоящее время не поддерживает данные, которые лежат в подпространстве меньшей размерности пространства, в котором они выражены. Для таких данных рассмотрите выполнение анализа главных компонент / снижения размерности и использование gaussian_kde с преобразованными данными.

Ссылки

[1] (1,2,3)

D.W. Scott, "Multivariate Density Estimation: Theory, Practice, and Visualization", John Wiley & Sons, New York, Chicester, 1992.

[2] (1,2)

Б.В. Сильверман, «Оценка плотности для статистики и анализа данных», Том 26, Монографии по статистике и прикладной вероятности, Chapman and Hall, Лондон, 1986.

[3]

Б.А. Турлах, «Выбор ширины окна в оценке плотности ядра: Обзор», CORE и Institut de Statistique, Том 19, стр. 1-33, 1993.

[4]

D.M. Bashtannyk and R.J. Hyndman, “Bandwidth selection for kernel conditional density estimation”, Computational Statistics & Data Analysis, Vol. 36, pp. 279-298, 2001.

[5]

Gray P. G., 1969, Journal of the Royal Statistical Society. Series A (General), 132, 272

[6]

Оценка плотности ядра. Википедия. https://en.wikipedia.org/wiki/Kernel_density_estimation

Примеры

Попробуйте в вашем браузере!

Сгенерируйте некоторые случайные двумерные данные:

>>> import numpy as np
>>> from scipy import stats
>>> def measure(n):
...     "Measurement model, return two coupled measurements."
...     m1 = np.random.normal(size=n)
...     m2 = np.random.normal(scale=0.5, size=n)
...     return m1+m2, m1-m2

>>> m1, m2 = measure(2000)
>>> xmin = m1.min()
>>> xmax = m1.max()
>>> ymin = m2.min()
>>> ymax = m2.max()

Выполните оценку плотности ядра на данных:

>>> X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
>>> positions = np.vstack([X.ravel(), Y.ravel()])
>>> values = np.vstack([m1, m2])
>>> kernel = stats.gaussian_kde(values)
>>> Z = np.reshape(kernel(positions).T, X.shape)

Построить результаты:

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.imshow(np.rot90(Z), cmap=plt.cm.gist_earth_r,
...           extent=[xmin, xmax, ymin, ymax])
>>> ax.plot(m1, m2, 'k.', markersize=2)
>>> ax.set_xlim([xmin, xmax])
>>> ax.set_ylim([ymin, ymax])
>>> plt.show()

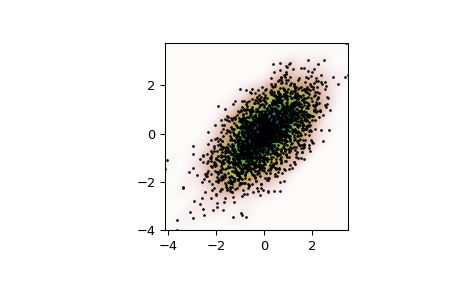
Сравнение с ручным KDE в точке:

>>> point = [1, 2]
>>> mean = values.T
>>> cov = kernel.factor**2 * np.cov(values)
>>> X = stats.multivariate_normal(cov=cov)
>>> res = kernel.pdf(point)
>>> ref = X.pdf(point - mean).sum() / len(mean)
>>> np.allclose(res, ref)
True

НазадОткрыть во вкладке