scipy.stats.

куртозис

scipy.stats.куртозис(a, ось=0, fisher=True, смещение=True, nan_policy='propagate', *, keepdims=False)

Вычислить эксцесс (Фишера или Пирсона) набора данных.

Эксцесс — это четвёртый центральный момент, делённый на квадрат дисперсии. Если используется определение Фишера, то из результата вычитается 3.0, чтобы получить 0.0 для нормального распределения.

Если bias равен False, то эксцесс вычисляется с использованием k-статистик, чтобы устранить смещение, возникающее из-за смещенных оценок моментов

Используйте kurtosistest чтобы проверить, достаточно ли результат близок к нормальному.

Параметры:

aмассив

Данные, для которых рассчитывается эксцесс.

осьint или None, по умолчанию: 0

Если это целое число, ось входных данных, по которой вычисляется статистика. Статистика каждого среза по оси (например, строки) входных данных появится в соответствующем элементе вывода. Если None, вход будет сведён в одномерный массив перед вычислением статистики.

fisherbool, необязательно

Если True, используется определение Фишера (нормальное ==> 0.0). Если False, используется определение Пирсона (нормальное ==> 3.0).

смещениеbool, необязательно

Если False, то вычисления корректируются на статистическое смещение.

nan_policy{‘propagate’, ‘omit’, ‘raise’}

Определяет, как обрабатывать входные значения NaN.

• propagate: если NaN присутствует в срезе оси (например, строке), вдоль которой вычисляется статистика, соответствующая запись вывода будет NaN.

• omit: NaN будут пропущены при выполнении расчета. Если в срезе оси, вдоль которого вычисляется статистика, остается недостаточно данных, соответствующая запись вывода будет NaN.

• raise: если присутствует NaN, то ValueError будет вызвано исключение.

keepdimsbool, по умолчанию: False

Если установлено значение True, оси, которые были сокращены, остаются в результате как размерности с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.

Возвращает:

куртозисмассив

Эксцесс значений вдоль оси, возвращающий NaN, где все значения равны.

Примечания

Начиная с SciPy 1.9, np.matrix входные данные (не рекомендуется для нового кода) преобразуются в np.ndarray перед выполнением вычисления. В этом случае результатом будет скаляр или np.ndarray подходящей формы вместо 2D np.matrix. Аналогично, хотя маскированные элементы маскированных массивов игнорируются, результатом будет скаляр или np.ndarray вместо маскированного массива с mask=False.

kurtosis имеет экспериментальную поддержку совместимых с Python Array API Standard бэкендов в дополнение к NumPy. Пожалуйста, рассмотрите тестирование этих функций, установив переменную окружения SCIPY_ARRAY_API=1 и предоставление массивов CuPy, PyTorch, JAX или Dask в качестве аргументов массива. Поддерживаются следующие комбинации бэкенда и устройства (или других возможностей).

Библиотека	CPU	GPU
NumPy	✅	н/д
CuPy	н/д	✅
PyTorch	✅	✅
JAX	⚠️ нет JIT	⚠️ нет JIT
Dask	⚠️ вычисляет граф	н/д

См. Поддержка стандарта array API для получения дополнительной информации.

Ссылки

[1]

Цвиллингер, Д. и Кокошка, С. (2000). CRC Стандартные таблицы и формулы вероятности и статистики. Chapman & Hall: Нью-Йорк. 2000.

Примеры

Попробуйте в вашем браузере!

В определении Фишера эксцесс нормального распределения равен нулю. В следующем примере эксцесс близок к нулю, потому что он был рассчитан на основе набора данных, а не из непрерывного распределения.

>>> import numpy as np
>>> from scipy.stats import norm, kurtosis
>>> data = norm.rvs(size=1000, random_state=3)
>>> kurtosis(data)
-0.06928694200380558

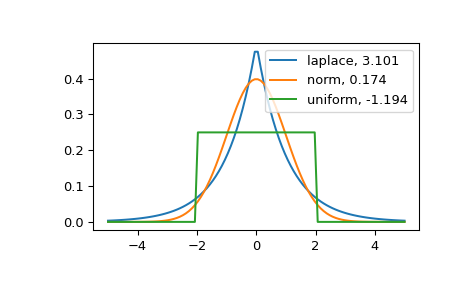
Распределение с более высоким эксцессом имеет более тяжёлый хвост. Нулевой эксцесс нормального распределения в определении Фишера может служить точкой отсчёта.

>>> import matplotlib.pyplot as plt
>>> import scipy.stats as stats
>>> from scipy.stats import kurtosis

>>> x = np.linspace(-5, 5, 100)
>>> ax = plt.subplot()
>>> distnames = ['laplace', 'norm', 'uniform']

>>> for distname in distnames:
...     if distname == 'uniform':
...         dist = getattr(stats, distname)(loc=-2, scale=4)
...     else:
...         dist = getattr(stats, distname)
...     data = dist.rvs(size=1000)
...     kur = kurtosis(data, fisher=True)
...     y = dist.pdf(x)
...     ax.plot(x, y, label="{}, {}".format(distname, round(kur, 3)))
...     ax.legend()

Распределение Лапласа имеет более тяжёлый хвост, чем нормальное распределение. Равномерное распределение (которое имеет отрицанный эксцесс) имеет самый тонкий хвост.

НазадОткрыть во вкладке