order_statistic#
- scipy.stats.order_statistic(X, /, *, r, n)[источник]#
Распределение вероятностей порядковой статистики
Возвращает случайную величину, следующую распределению, лежащему в основе \(r^{\text{th}}\) порядковая статистика выборки из \(n\) наблюдения случайной величины \(X\).
- Параметры:
- XContinuousDistribution
Случайная величина \(X\)
- rarray_like
(Положительное целое) ранг порядковой статистики \(r\)
- narray_like
(положительное целое) размер выборки \(n\)
- Возвращает:
- YContinuousDistribution
Случайная величина, следующая распределению предписанной порядковой статистики.
Примечания
Если мы сделаем \(n\) наблюдения непрерывной случайной величины \(X\) и сортировка их в порядке возрастания \(X_{(1)}, \dots, X_{(r)}, \dots, X_{(n)}\), \(X_{(r)}\) известен как \(r^{\text{th}}\) порядковая статистика.
Если PDF, CDF и CCDF, лежащие в основе математики:X обозначаются \(f\), \(F\), и \(F'\), соответственно, тогда PDF, лежащий в основе math:X_{(r)} задается формулой:
\[f_r(x) = \frac{n!}{(r-1)! (n-r)!} f(x) F(x)^{r-1} F'(x)^{n - r}\]CDF и другие методы распределения, лежащего в основе \(X_{(r)}\) вычисляются с использованием того факта, что \(X = F^{-1}(U)\), где \(U\) является стандартной равномерной случайной величиной, и что порядковые статистики наблюдений U следуют бета-распределению, \(B(r, n - r + 1)\).
Ссылки
[1]Порядковая статистика. Википедия. https://en.wikipedia.org/wiki/Order_statistic
Примеры
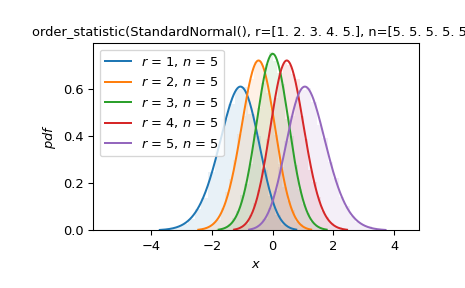
Предположим, нас интересуют порядковые статистики выборок размера пять, извлечённых из стандартного нормального распределения. Постройте PDF, лежащий в основе каждой порядковой статистики, и сравните с нормализованной гистограммой из симуляции.
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy import stats >>> >>> X = stats.Normal() >>> data = X.sample(shape=(10000, 5)) >>> sorted = np.sort(data, axis=1) >>> Y = stats.order_statistic(X, r=[1, 2, 3, 4, 5], n=5) >>> >>> ax = plt.gca() >>> colors = plt.rcParams['axes.prop_cycle'].by_key()['color'] >>> for i in range(5): ... y = sorted[:, i] ... ax.hist(y, density=True, bins=30, alpha=0.1, color=colors[i]) >>> Y.plot(ax=ax) >>> plt.show()