scipy.stats.

ppcc_plot

scipy.stats.ppcc_plot(x, a, b, dist='tukeylambda', plot=None, N=80)

Вычислить и, возможно, построить график коэффициента корреляции вероятностного графика.

Коэффициент корреляции вероятностного графика (PPCC) может использоваться для определения оптимального параметра формы для однопараметрического семейства распределений. Он не может использоваться для распределений без параметров формы (как нормальное распределение) или с несколькими параметрами формы.

По умолчанию распределение Тьюки-Лямбда (stats.tukeylambda) используется. График PPCC Тьюки-Лямбда интерполирует от длиннохвостых к короткохвостым распределениям через приблизительно нормальное и поэтому особенно полезен на практике.

Параметры:

xarray_like

Входной массив.

a, bскаляр

Нижняя и верхняя границы параметра формы для использования.

diststr или экземпляр stats.distributions, опционально

Имя распределения или функции распределения. Объекты, достаточно похожие на экземпляр stats.distributions (т.е. имеющие ppf method) также принимаются. По умолчанию 'tukeylambda'.

plotобъект, опционально

Если задано, строит график PPCC в зависимости от параметра формы. plot является объектом, который должен иметь методы "plot" и "text". matplotlib.pyplot модуль или объект Matplotlib Axes можно использовать, или пользовательский объект с теми же методами. По умолчанию None, что означает, что график не создается.

Nint, необязательный

Количество точек на горизонтальной оси (равномерно распределённых от a to b).

Возвращает:

сингулярные значенияndarray

Значения формы, для которых ppcc был рассчитан.

ppccndarray

Вычисленные значения коэффициента корреляции вероятностного графика.

Смотрите также

ppcc_max, probplot, boxcox_normplot, tukeylambda

Ссылки

J.J. Filliben, "Тест коэффициента корреляции вероятностного графика для нормальности", Technometrics, Vol. 17, pp. 111-117, 1975.

Примеры

Попробуйте в вашем браузере!

Сначала мы генерируем случайные данные из распределения Вейбулла с параметром формы 2.5 и строим гистограмму данных:

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> c = 2.5
>>> x = stats.weibull_min.rvs(c, scale=4, size=2000, random_state=rng)

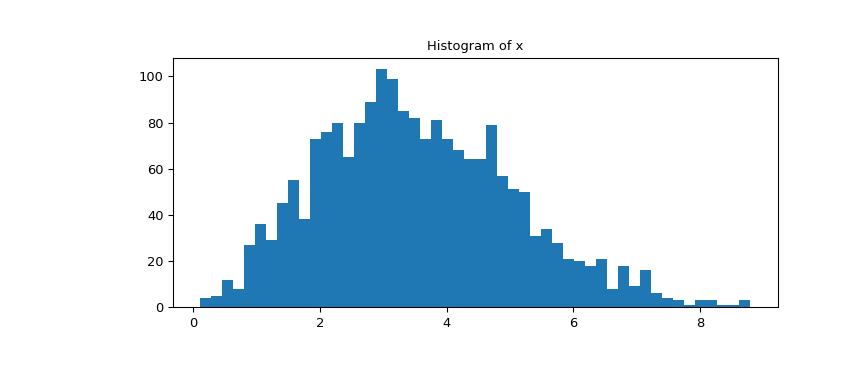
Взгляните на гистограмму данных.

>>> fig1, ax = plt.subplots(figsize=(9, 4))
>>> ax.hist(x, bins=50)
>>> ax.set_title('Histogram of x')
>>> plt.show()

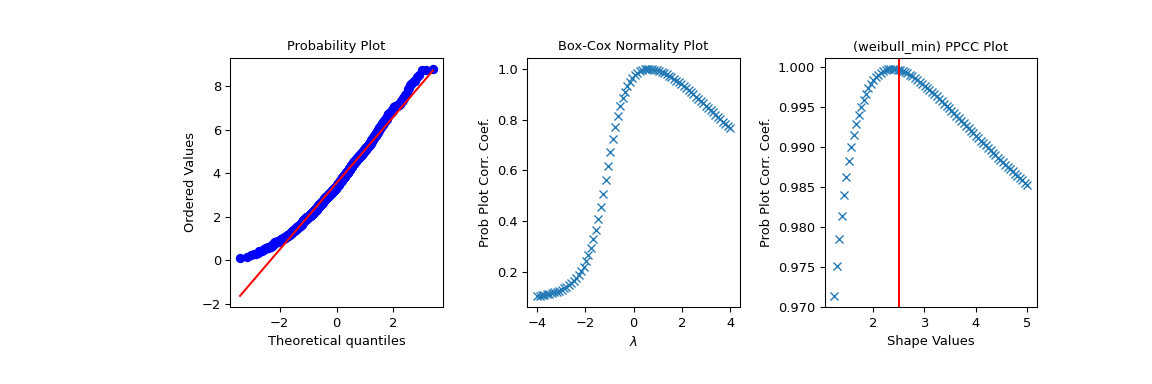
Теперь мы исследуем эти данные с помощью графика PPCC, а также связанных вероятностного графика и норм-графика Бокса-Кокса. Красная линия проведена там, где мы ожидаем максимальное значение PPCC (при параметре формы c использованный выше):

>>> fig2 = plt.figure(figsize=(12, 4))
>>> ax1 = fig2.add_subplot(1, 3, 1)
>>> ax2 = fig2.add_subplot(1, 3, 2)
>>> ax3 = fig2.add_subplot(1, 3, 3)
>>> res = stats.probplot(x, plot=ax1)
>>> res = stats.boxcox_normplot(x, -4, 4, plot=ax2)
>>> res = stats.ppcc_plot(x, c/2, 2*c, dist='weibull_min', plot=ax3)
>>> ax3.axvline(c, color='r')
>>> plt.show()

НазадОткрыть во вкладке