scipy.stats.

rv_discrete

класс scipy.stats.rv_discrete(a=0, b=inf, имя=None, badvalue=None, moment_tol=1e-08, values=None, inc=1, длинное имя=None, формы=None, seed=None)

Универсальный класс дискретной случайной величины, предназначенный для наследования.

rv_discrete является базовым классом для создания конкретных классов распределений и экземпляров для дискретных случайных величин. Также может использоваться для создания произвольного распределения, заданного списком точек поддержки и соответствующих вероятностей.

Параметры:

afloat, опционально

Нижняя граница носителя распределения, по умолчанию: 0

bfloat, опционально

Верхняя граница поддержки распределения, по умолчанию: плюс бесконечность

moment_tolfloat, опционально

Допуск для общего расчета моментов.

valuesкортеж из двух array_like, опционально

(xk, pk) где xk являются целыми числами и pk — это ненулевые вероятности между 0 и 1 с sum(pk) = 1. xk и pk должны иметь одинаковую форму, и xk должны быть уникальными.

incцелое число, опционально

Приращение для поддержки распределения. По умолчанию равно 1. (другие значения не тестировались)

badvaluefloat, опционально

Значение в результирующих массивах, которое указывает на значение, для которого нарушено некоторое ограничение аргумента, по умолчанию np.nan.

имяstr, optional

Имя экземпляра. Эта строка используется для создания стандартного примера для распределений.

длинное имяstr, optional

Эта строка используется как часть первой строки документации, возвращаемой когда подкласс не имеет собственной документации. Примечание: длинное имя существует для обратной совместимости, не используйте для новых подклассов.

формыstr, optional

Форма распределения. Например, "m, n" для распределения, которое принимает два целых числа в качестве двух аргументов формы для всех своих методов. Если не указано, параметры формы будут выведены из сигнатур приватных методов. _pmf и _cdf экземпляра.

seed{None, int, numpy.random.Generator, numpy.random.RandomState, опционально

Если seed равно None (или np.random), numpy.random.RandomState используется синглтон. Если seed является int, новый RandomState используется экземпляр, инициализированный с seed. Если seed уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Атрибуты:

a, bfloat, опционально

Нижняя/верхняя граница поддержки несдвинутого/немасштабированного распределения. Это значение не затрагивается loc и scale параметры. Чтобы вычислить носитель сдвинутого/масштабированного распределения, используйте support метод.

Методы

rvs(*args, **kwargs)	Случайные величины заданного типа.
pmf(k, *args, **kwds)	Функция вероятности в точке k для заданной случайной величины.
logpmf(k, *args, **kwds)	Логарифм функции вероятности в точке k для данного случайного вектора.
cdf(k, *args, **kwds)	Функция кумулятивного распределения заданной случайной величины.
logcdf(k, *args, **kwds)	Логарифм функции распределения в точке k для данного СВ.
sf(k, *args, **kwds)	Функция выживания (1 - cdf) в точке k для данного RV.
logsf(k, *args, **kwds)	Логарифм функции выживания данного случайного вектора.
ppf(q, *args, **kwds)	Процентная точка функции (обратная cdf) при q заданного случайного распределения.
isf(q, *args, **kwds)	Обратная функция выживания (обратная к sf) при q заданного случайного распределения.
moment(order, *args, **kwds)	нецентральный момент распределения указанного порядка.
stats(*args, **kwds)	Некоторые статистики заданного случайного вектора.
entropy(*args, **kwds)	Дифференциальная энтропия случайной величины.
expect([func, args, loc, lb, ub, ...])	Вычислить математическое ожидание функции относительно распределения для дискретного распределения путем численного суммирования.
median(*args, **kwds)	Медиана распределения.
mean(*args, **kwds)	Среднее распределения.
std(*args, **kwds)	Стандартное отклонение распределения.
var(*args, **kwds)	Дисперсия распределения.
interval(confidence, *args, **kwds)	Доверительный интервал с равными площадями вокруг медианы.
__call__(*args, **kwds)	Зафиксировать распределение для заданных аргументов.
support(*args, **kwargs)	Носитель распределения.

Примечания

Этот класс похож на rv_continuous. Является ли параметр формы допустимым, определяется _argcheck метод (который по умолчанию проверяет, что его аргументы строго положительны.) Основные различия следующие.

• Носитель распределения является множеством целых чисел.

• Вместо функции плотности вероятности, pdf (и соответствующий приватный _pdf), этот класс определяет функция вероятности массы, pmf (и соответствующий приватный _pmf.)

• Нет scale параметр.

• Реализации методов по умолчанию (например, _cdf) не предназначены для распределений с носителем, неограниченным снизу (т.е. a=-np.inf), поэтому они должны быть переопределены.

Чтобы создать новое дискретное распределение, мы сделаем следующее:

>>> from scipy.stats import rv_discrete
>>> class poisson_gen(rv_discrete):
...     "Poisson distribution"
...     def _pmf(self, k, mu):
...         return exp(-mu) * mu**k / factorial(k)

и создать экземпляр:

>>> poisson = poisson_gen(name="poisson")

Обратите внимание, что выше мы определили распределение Пуассона в стандартной форме. Сдвиг распределения можно выполнить, предоставив loc параметр методам экземпляра. Например, poisson.pmf(x, mu, loc) делегирует работу poisson._pmf(x-loc, mu).

Дискретные распределения из списка вероятностей

Альтернативно, вы можете построить произвольную дискретную случайную величину, определённую на конечном наборе значений xk с Prob{X=xk} = pk используя values ключевой аргумент для rv_discrete конструктор.

Глубокое копирование / Сериализация

Если распределение или замороженное распределение глубоко копируется (пиклируется/распиклируется, и т.д.), любой базовый генератор случайных чисел копируется вместе с ним. Следствием является то, что если распределение полагается на синглтон RandomState перед копированием, оно будет полагаться на копию этого случайного состояния после копирования, и np.random.seed больше не будет управлять состоянием.

Примеры

Попробуйте в вашем браузере!

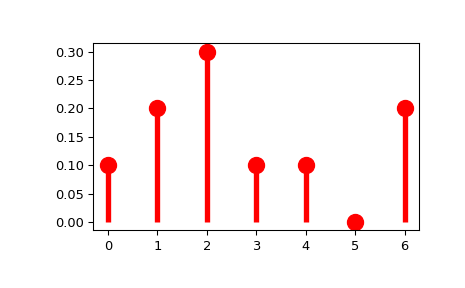
Пользовательское дискретное распределение:

>>> import numpy as np
>>> from scipy import stats
>>> xk = np.arange(7)
>>> pk = (0.1, 0.2, 0.3, 0.1, 0.1, 0.0, 0.2)
>>> custm = stats.rv_discrete(name='custm', values=(xk, pk))
>>>
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 1)
>>> ax.plot(xk, custm.pmf(xk), 'ro', ms=12, mec='r')
>>> ax.vlines(xk, 0, custm.pmf(xk), colors='r', lw=4)
>>> plt.show()

Генерация случайных чисел:

>>> R = custm.rvs(size=100)

НазадОткрыть во вкладке