scipy.stats.sampling.

DiscreteGuideTable#

класс scipy.stats.sampling.DiscreteGuideTable(dist, *, область определения=None, guide_factor=1, random_state=None)#

Метод дискретной таблицы направляющих.

Метод Discrete Guide Table производит выборку из произвольных, но конечных векторов вероятностей. Он использует вектор вероятностей размера \(N\) или функцию вероятностной массы с конечным носителем для генерации случайных чисел из распределения. Discrete Guide Table имеет очень медленную настройку (линейную с длиной вектора), но обеспечивает очень быструю выборку.

Параметры:

distarray_like или объект, опционально

Вероятностный вектор (PV) распределения. Если PV недоступен, экземпляр класса с pmf ожидается метод. Сигнатура PMF ожидается как: def pmf(self, k: int) -> float. т.е. он должен принимать целое число Python и возвращать число с плавающей точкой Python.

область определенияint, необязательный

Носитель PMF. Если вектор вероятностей (pv) недоступен, должна быть задана конечная область. Т.е. PMF должен иметь конечную поддержку. По умолчанию None. Когда None:

Если support метод предоставляется объектом распределения dist, используется для установки области определения распределения.
В противном случае предполагается, что носитель (0, len(pv)). Когда этот параметр передается в сочетании с вектором вероятности, domain[0] используется для перемещения распределения из (0, len(pv)) to (domain[0], domain[0]+len(pv)) и domain[1] игнорируется. См. Примечания и учебник для более подробного объяснения.

guide_factor: int, optional

Размер таблицы направляющих относительно длины PV. Большие таблицы направляющих приводят к более быстрому времени генерации, но требуют более дорогой настройки. Размеры больше 3 не рекомендуются. Если относительный размер установлен в 0, используется последовательный поиск. По умолчанию 1.

random_state{None, int, numpy.random.Generator,

numpy.random.RandomState, опционально

Генератор случайных чисел NumPy или seed для базового генератора случайных чисел NumPy, используемого для генерации потока равномерных случайных чисел. Если random_state равно None (или np.random), numpy.random.RandomState используется синглтон. Если random_state является int, новый RandomState используется экземпляр, инициализированный с random_state. Если random_state уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Методы

`ppf`(u)	PPF заданного распределения.
`rvs`([size, random_state])	Выборка из распределения.
`set_random_state`([random_state])	Установить базовый генератор равномерных случайных чисел.

Примечания

Этот метод работает, когда доступен либо конечный вектор вероятностей, либо функция вероятности распределения. Если доступна только функция вероятности, то конечный область определения (support) PMF также должна быть задана. Рекомендуется сначала получить вектор вероятностей, вычислив PMF в каждой точке области определения, а затем использовать его вместо этого.

DGT выбирает из произвольных, но конечных вероятностных векторов. Случайные числа генерируются методом инверсии, т.е.

Сгенерировать случайное число U ~ U(0,1).
Найти наименьшее целое I такое, что F(I) = P(X<=I) >= U.

Шаг (2) является ключевым. Использование последовательного поиска требует O(E(X)) сравнений, где E(X) - математическое ожидание распределения. Однако индексированный поиск использует таблицу-указатель для перехода к некоторому I' <= I около I, чтобы найти X за постоянное время. Действительно, ожидаемое количество сравнений сокращается до 2, когда таблица-указатель имеет тот же размер, что и вектор вероятностей (это значение по умолчанию). Для больших таблиц это число становится меньше (но всегда больше 1), для меньших таблиц - больше. В предельном случае размера таблицы 1 алгоритм просто выполняет последовательный поиск.

С другой стороны, время настройки таблицы-гида составляет O(N), где N обозначает длину вектора вероятностей (для размера 1 предварительная обработка не требуется). Более того, для очень больших таблиц-гидов эффекты памяти могут даже снизить скорость алгоритма. Поэтому мы не рекомендуем использовать таблицы-гиды, которые более чем в три раза превышают заданный вектор вероятностей. Если нужно сгенерировать только несколько случайных чисел, (гораздо) меньшие размеры таблиц лучше. Размер таблицы-гида относительно длины заданного вектора вероятностей может быть установлен с помощью guide_factor параметр.

Если задан вероятностный вектор, он должен быть одномерным массивом неотрицательных чисел с плавающей запятой без каких-либо inf или nan значения. Также должен быть хотя бы один ненулевой элемент, иначе будет вызвано исключение.

По умолчанию вектор вероятностей индексируется, начиная с 0. Однако это можно изменить, передав domain параметр. Когда domain при использовании в комбинации с PV, это приводит к перемещению распределения из (0, len(pv)) to (domain[0], domain[0] + len(pv)). domain[1] игнорируется в этом случае.

Ссылки

[1]

Справочное руководство UNU.RAN, раздел 5.8.4, "DGT - (Дискретный) метод таблицы направляющих (индексированный поиск)" https://statmath.wu.ac.at/unuran/doc/unuran.html#DGT

[2]

H.C. Chen и Y. Asau (1974). О генерации случайных величин из эмпирического распределения, AIIE Trans. 6, стр. 163-166.

Примеры

>>> from scipy.stats.sampling import DiscreteGuideTable
>>> import numpy as np

Чтобы создать генератор случайных чисел с использованием вектора вероятностей, используйте:

>>> pv = [0.1, 0.3, 0.6]
>>> urng = np.random.default_rng()
>>> rng = DiscreteGuideTable(pv, random_state=urng)

Генератор случайных чисел был настроен. Теперь мы можем использовать rvs метод для генерации выборок из распределения:

>>> rvs = rng.rvs(size=1000)

Чтобы проверить, что случайные величины следуют заданному распределению, можно использовать критерий хи-квадрат (как меру соответствия):

>>> from scipy.stats import chisquare
>>> _, freqs = np.unique(rvs, return_counts=True)
>>> freqs = freqs / np.sum(freqs)
>>> freqs
array([0.092, 0.355, 0.553])
>>> chisquare(freqs, pv).pvalue
0.9987382966178464

Поскольку p-значение очень высоко, мы не можем отвергнуть нулевую гипотезу о том, что наблюдаемые частоты совпадают с ожидаемыми частотами. Следовательно, мы можем безопасно предположить, что величины были сгенерированы из заданного распределения. Обратите внимание, что это проверяет корректность алгоритма, а не качество выборок.

Если PV недоступен, также можно передать экземпляр класса с методом PMF и конечной областью определения.

>>> urng = np.random.default_rng()
>>> from scipy.stats import binom
>>> n, p = 10, 0.2
>>> dist = binom(n, p)
>>> rng = DiscreteGuideTable(dist, random_state=urng)

Теперь мы можем выполнить выборку из распределения, используя rvs метод а также измеряет качество соответствия выборок:

>>> rvs = rng.rvs(1000)
>>> _, freqs = np.unique(rvs, return_counts=True)
>>> freqs = freqs / np.sum(freqs)
>>> obs_freqs = np.zeros(11)  # some frequencies may be zero.
>>> obs_freqs[:freqs.size] = freqs
>>> pv = [dist.pmf(i) for i in range(0, 11)]
>>> pv = np.asarray(pv) / np.sum(pv)
>>> chisquare(obs_freqs, pv).pvalue
0.9999999999999989

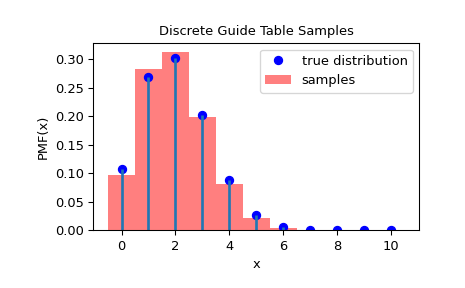
Чтобы проверить, что выборки были взяты из правильного распределения, мы можем визуализировать гистограмму выборок:

>>> import matplotlib.pyplot as plt
>>> rvs = rng.rvs(1000)
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> x = np.arange(0, n+1)
>>> fx = dist.pmf(x)
>>> fx = fx / fx.sum()
>>> ax.plot(x, fx, 'bo', label='true distribution')
>>> ax.vlines(x, 0, fx, lw=2)
>>> ax.hist(rvs, bins=np.r_[x, n+1]-0.5, density=True, alpha=0.5,
...         color='r', label='samples')
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('PMF(x)')
>>> ax.set_title('Discrete Guide Table Samples')
>>> plt.legend()
>>> plt.show()

../../_images/scipy-stats-sampling-DiscreteGuideTable-1_00_00.png

Чтобы установить размер таблицы направляющих, используйте guide_factor ключевой аргумент. Это устанавливает размер таблицы направляющих относительно вектора вероятности

>>> rng = DiscreteGuideTable(pv, guide_factor=1, random_state=urng)

Чтобы вычислить PPF биномиального распределения с \(n=4\) и \(p=0.1\): мы можем настроить таблицу направлений следующим образом:

>>> n, p = 4, 0.1
>>> dist = binom(n, p)
>>> rng = DiscreteGuideTable(dist, random_state=42)
>>> rng.ppf(0.5)
0.0