scipy.stats.sampling.

NumericalInverseHermite

класс scipy.stats.sampling.NumericalInverseHermite(dist, *, область определения=None, порядок=3, u_resolution=1e-12, construction_points=None, random_state=None)

Интерполяция Эрмита на основе инверсии CDF (HINV).

HINV — это вариант численной инверсии, где обратная CDF аппроксимируется с помощью интерполяции Эрмита, т.е. интервал [0,1] разбивается на несколько интервалов, и в каждом интервале обратная CDF аппроксимируется полиномами, построенными на основе значений CDF и PDF на границах интервалов. Это позволяет улучшить точность, разбивая конкретный интервал без пересчётов в незатронутых интервалах. Реализованы три типа сплайнов: линейная, кубическая и квинтическая интерполяция. Для линейной интерполяции требуется только CDF. Кубическая интерполяция также требует PDF, а квинтическая — PDF и её производную.

Эти сплайны должны быть вычислены на этапе настройки. Однако это работает только для распределений с ограниченной областью; для распределений с неограниченной областью хвосты обрезаются так, что вероятность для хвостовых областей мала по сравнению с заданным u-разрешением.

Метод не является точным, так как он производит только случайные величины аппроксимированного распределения. Тем не менее, максимальная численная ошибка в "u-направлении" (т.е. |U - CDF(X)| где X является приблизительным процентилем, соответствующим квантилю U т.е. X = approx_ppf(U)) может быть установлено на требуемое разрешение (в пределах машинной точности). Обратите внимание, что очень маленькие значения u-разрешения возможны, но могут увеличить стоимость шага настройки.

Параметры:

distobject

Экземпляр класса с cdf и, возможно, pdf и dpdf метод.

• cdf: Функция распределения (CDF) распределения. Ожидается, что сигнатура CDF будет: def cdf(self, x: float) -> float. т.е. CDF должна принимать Python float и возвращать Python float.

• pdf: PDF распределения. Этот метод является опциональным, когда order=1. Должна иметь ту же сигнатуру, что и PDF.

• dpdf: Производная PDF по переменной (т.е. x). Этот метод является необязательным с order=1 или order=3. Должна иметь ту же сигнатуру, что и CDF.

область определениясписок или кортеж длины 2, опционально

Носитель распределения. По умолчанию None. Когда None:

• Если support метод предоставляется объектом распределения dist, используется для установки области определения распределения.

• В противном случае предполагается, что носитель \((-\infty, \infty)\).

порядокint, по умолчанию: 3

Установите порядок интерполяции Эрмита. Допустимые порядки: 1, 3 и 5. Допустимые порядки: 1, 3 и 5. Обратите внимание, что порядок больше 1 требует плотности распределения, а порядок больше 3 даже требует производной плотности. Использование порядка 1 для большинства распределений приводит к огромному количеству интервалов и поэтому не рекомендуется. Если максимальная ошибка в направлении u очень мала (скажем, меньше 1.e-10), рекомендуется порядок 5, так как он приводит к значительно меньшему количеству точек проектирования, при условии отсутствия полюсов или тяжелых хвостов.

u_resolutionfloat, по умолчанию: 1e-12

Установить максимально допустимую u-ошибку. Обратите внимание, что разрешение большинства источников равномерных случайных чисел составляет 2^-32 = 2.3e-10. Таким образом, значение 1.e-10 приводит к алгоритму инверсии, который можно назвать точным. Для большинства симуляций также достаточно немного больших значений максимальной ошибки. По умолчанию 1e-12.

construction_pointsarray_like, необязательный

Установить начальные точки построения (узлы) для интерполяции Эрмита. Поскольку возможная максимальная ошибка оценивается только при настройке, может потребоваться установить некоторые специальные точки проектирования для вычисления интерполяции Эрмита, чтобы гарантировать, что максимальная u-ошибка не может быть больше желаемой. Такие точки — это точки, где плотность не дифференцируема или имеет локальный экстремум.

random_state{None, int, numpy.random.Generator,

numpy.random.RandomState, опционально

Генератор случайных чисел NumPy или seed для базового генератора случайных чисел NumPy, используемого для генерации потока равномерных случайных чисел. Если random_state равно None (или np.random), numpy.random.RandomState используется синглтон. Если random_state является int, новый RandomState используется экземпляр, инициализированный с random_state. Если random_state уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Атрибуты:

intervals

Получить количество узлов (точек проектирования), используемых для интерполяции Эрмита в объекте-генераторе.

midpoint_error

Методы

ppf(u)	Приближенная PPF заданного распределения.
qrvs([size, d, qmc_engine])	Квазислучайные величины заданной случайной величины.
rvs([size, random_state])	Выборка из распределения.
set_random_state([random_state])	Установить базовый генератор равномерных случайных чисел.
u_error([sample_size])	Оценить u-ошибку аппроксимации с помощью метода Монте-Карло.

Примечания

NumericalInverseHermite аппроксимирует обратную функцию непрерывного статистического распределения CDF с помощью сплайна Эрмита. Порядок сплайна Эрмита может быть задан передачей порядок параметр.

Как описано в [1], он начинается с вычисления PDF и CDF распределения на сетке квантилей x в пределах носителя распределения. Он использует результаты для подгонки сплайна Эрмита H такой, что H(p) == x, где p является массивом процентилей, соответствующих квантилям x. Поэтому сплайн аппроксимирует обратную функцию CDF распределения с машинной точностью на перцентилях p, но обычно сплайн будет менее точным в средних точках между процентилями:

p_mid = (p[:-1] + p[1:])/2

так что сетка квантилей уточняется по мере необходимости для уменьшения максимальной "u-ошибки":

u_error = np.max(np.abs(dist.cdf(H(p_mid)) - p_mid))

ниже указанного допуска u_resolution. Уточнение останавливается, когда достигается требуемая точность или когда количество интервалов сетки после следующего уточнения может превысить максимально допустимое количество интервалов, которое составляет 100000.

Ссылки

[1]

Хёрманн, Вольфганг, и Йозеф Лейдольд. «Непрерывная генерация случайных величин с помощью быстрой численной инверсии». ACM Transactions on Modeling and Computer Simulation (TOMACS) 13.4 (2003): 347-362.

[2]

Руководство по UNU.RAN, Раздел 5.3.5, “HINV - инверсия CDF на основе интерполяции Эрмита”, https://statmath.wu.ac.at/software/unuran/doc/unuran.html#HINV

Примеры

Попробуйте в вашем браузере!

>>> from scipy.stats.sampling import NumericalInverseHermite
>>> from scipy.stats import norm, genexpon
>>> from scipy.special import ndtr
>>> import numpy as np

Чтобы создать генератор для выборки из стандартного нормального распределения, сделайте:

>>> class StandardNormal:
...     def pdf(self, x):
...        return 1/np.sqrt(2*np.pi) * np.exp(-x**2 / 2)
...     def cdf(self, x):
...        return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, random_state=urng)

The NumericalInverseHermite имеет метод, который аппроксимирует PPF распределения.

>>> rng = NumericalInverseHermite(dist)
>>> p = np.linspace(0.01, 0.99, 99) # percentiles from 1% to 99%
>>> np.allclose(rng.ppf(p), norm.ppf(p))
True

В зависимости от реализации метода случайной выборки распределения, сгенерированные случайные величины могут быть почти идентичными при одинаковом случайном состоянии.

>>> dist = genexpon(9, 16, 3)
>>> rng = NumericalInverseHermite(dist)
>>> # `seed` ensures identical random streams are used by each `rvs` method
>>> seed = 500072020
>>> rvs1 = dist.rvs(size=100, random_state=np.random.default_rng(seed))
>>> rvs2 = rng.rvs(size=100, random_state=np.random.default_rng(seed))
>>> np.allclose(rvs1, rvs2)
True

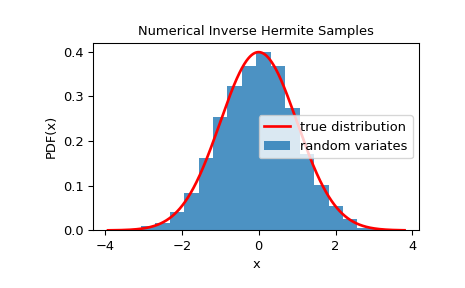
Чтобы проверить, что случайные величины близко следуют заданному распределению, можно посмотреть на его гистограмму:

>>> import matplotlib.pyplot as plt
>>> dist = StandardNormal()
>>> rng = NumericalInverseHermite(dist)
>>> rvs = rng.rvs(10000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = norm.pdf(x)
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Numerical Inverse Hermite Samples')
>>> plt.legend()
>>> plt.show()

Учитывая производную PDF по переменной (т.е. x), мы можем использовать интерполяцию Эрмита пятой степени для аппроксимации PPF, передавая порядок параметр:

>>> class StandardNormal:
...     def pdf(self, x):
...        return 1/np.sqrt(2*np.pi) * np.exp(-x**2 / 2)
...     def dpdf(self, x):
...        return -1/np.sqrt(2*np.pi) * x * np.exp(-x**2 / 2)
...     def cdf(self, x):
...        return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, order=5, random_state=urng)

Более высокие порядки приводят к меньшему количеству интервалов:

>>> rng3 = NumericalInverseHermite(dist, order=3)
>>> rng5 = NumericalInverseHermite(dist, order=5)
>>> rng3.intervals, rng5.intervals
(3000, 522)

Ошибку u можно оценить, вызвав u_error метод. Он запускает небольшое моделирование Монте-Карло для оценки u-ошибки. По умолчанию используется 100 000 образцов. Это можно изменить, передав sample_size аргумент:

>>> rng1 = NumericalInverseHermite(dist, u_resolution=1e-10)
>>> rng1.u_error(sample_size=1000000)  # uses one million samples
UError(max_error=9.53167544892608e-11, mean_absolute_error=2.2450136432146864e-11)

Это возвращает namedtuple, который содержит максимальную u-ошибку и среднюю абсолютную u-ошибку.

U-ошибку можно уменьшить, снизив u-разрешение (максимально допустимая u-ошибка):

>>> rng2 = NumericalInverseHermite(dist, u_resolution=1e-13)
>>> rng2.u_error(sample_size=1000000)
UError(max_error=9.32027892364129e-14, mean_absolute_error=1.5194172675685075e-14)

Обратите внимание, что это достигается за счет увеличения времени настройки и количества интервалов.

>>> rng1.intervals
1022
>>> rng2.intervals
5687
>>> from timeit import timeit
>>> f = lambda: NumericalInverseHermite(dist, u_resolution=1e-10)
>>> timeit(f, number=1)
0.017409582000254886  # may vary
>>> f = lambda: NumericalInverseHermite(dist, u_resolution=1e-13)
>>> timeit(f, number=1)
0.08671202100003939  # may vary

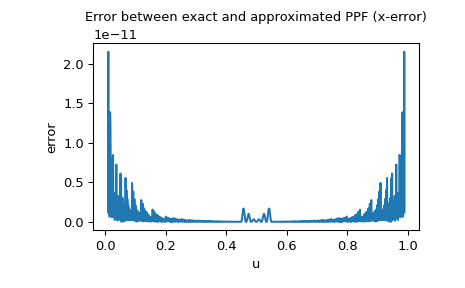
Поскольку PPF нормального распределения доступен как специальная функция, мы также можем проверить x-ошибку, т.е. разницу между аппроксимированным PPF и точным PPF:

>>> import matplotlib.pyplot as plt
>>> u = np.linspace(0.01, 0.99, 1000)
>>> approxppf = rng.ppf(u)
>>> exactppf = norm.ppf(u)
>>> error = np.abs(exactppf - approxppf)
>>> plt.plot(u, error)
>>> plt.xlabel('u')
>>> plt.ylabel('error')
>>> plt.title('Error between exact and approximated PPF (x-error)')
>>> plt.show()

НазадОткрыть во вкладке