TransformedDensityRejection#
- класс scipy.stats.sampling.TransformedDensityRejection(dist, *, mode=None, центр=None, область определения=None, c=-0.5, construction_points=30, use_dars=True, max_squeeze_hat_ratio=0.99, random_state=None)#
Метод преобразованного отклонения плотности (TDR).
TDR — это метод принятия/отклонения, который использует вогнутость преобразованной плотности для автоматического построения функции-шапки и сжатия. Большинство универсальных алгоритмов очень медленны по сравнению со специализированными алгоритмами для конкретного распределения. Быстрые алгоритмы имеют медленную настройку и требуют больших таблиц. Цель этого универсального метода — предоставить алгоритм, который не слишком медленный и требует лишь короткой настройки. Этот метод может быть применён к одномерным и унимодальным непрерывным распределениям с T-вогнутой функцией плотности. См. [1] и [2] для более подробной информации.
- Параметры:
- distobject
Экземпляр класса с
pdfиdpdfметоды.pdf: PDF распределения. Сигнатура PDF ожидается как:def pdf(self, x: float) -> float. т.е. PDF должна принимать число с плавающей точкой Python и возвращать число с плавающей точкой Python. Она не должна интегрироваться в 1, т.е. PDF не обязательно должна быть нормализована.dpdf: Производная PDF по x (т.е. переменной). Должна иметь ту же сигнатуру, что и PDF.
- modefloat, опционально
(Точная) Мода распределения. По умолчанию
None.- центрfloat, опционально
Приблизительное расположение моды или среднего распределения. Это расположение даёт информацию об основной части PDF и используется для избежания численных проблем. По умолчанию
None.- область определениясписок или кортеж длины 2, опционально
Носитель распределения. По умолчанию
None. КогдаNone:Если
supportметод предоставляется объектом распределения dist, используется для установки области определения распределения.В противном случае предполагается, что носитель \((-\infty, \infty)\).
- c{-0.5, 0.}, опционально
Установить параметр
cдля функции преобразованияT. По умолчанию -0.5. Преобразование PDF должно быть вогнутым, чтобы построить функцию-шапку. Такой PDF называется T-вогнутым. В настоящее время поддерживаются следующие преобразования:\[\begin{split}c = 0.: T(x) &= \log(x)\\ c = -0.5: T(x) &= \frac{1}{\sqrt{x}} \text{ (Default)}\end{split}\]- construction_pointsint или array_like, необязательно
Если целое число, оно определяет количество точек построения. Если это массивоподобный объект, элементы массива используются как точки построения. По умолчанию 30.
- use_darsbool, необязательно
Если True, используется "дерандомизированное адаптивное режекторное сэмплирование" (DARS) в настройке. См. [1] для подробностей алгоритма DARS. По умолчанию True.
- max_squeeze_hat_ratiofloat, опционально
Установить верхнюю границу для отношения (площадь под squeeze) / (площадь под hat). Это должно быть число между 0 и 1. По умолчанию 0.99.
- random_state{None, int,
numpy.random.Generator, numpy.random.RandomState, опциональноГенератор случайных чисел NumPy или seed для базового генератора случайных чисел NumPy, используемого для генерации потока равномерных случайных чисел. Если random_state равно None (или np.random),
numpy.random.RandomStateиспользуется синглтон. Если random_state является int, новыйRandomStateиспользуется экземпляр, инициализированный с random_state. Если random_state уже являетсяGeneratorилиRandomStateэкземпляр, тогда этот экземпляр используется.
- Атрибуты:
hat_areaПолучить площадь под «шляпой» для генератора.
squeeze_areaПолучить область под сжатием для генератора.
squeeze_hat_ratioПолучите текущее соотношение (площадь под сжатием) / (площадь под крышкой) для генератора.
Методы
ppf_hat(u)Вычислить обратную функцию CDF распределения-шляпы в u.
rvs([size, random_state])Выборка из распределения.
set_random_state([random_state])Установить базовый генератор равномерных случайных чисел.
Ссылки
[1] (1,2)Руководство по UNU.RAN, Раздел 5.3.16, 'TDR - Transformed Density Rejection', http://statmath.wu.ac.at/software/unuran/doc/unuran.html#TDR
[2]Хёрманн, Вольфганг. «Техника отклонения для выборки из T-вогнутых распределений.» ACM Transactions on Mathematical Software (TOMS) 21.2 (1995): 182-193
[3]W.R. Gilks и P. Wild (1992). Adaptive rejection sampling for Gibbs sampling, Applied Statistics 41, стр. 337-348.
Примеры
>>> from scipy.stats.sampling import TransformedDensityRejection >>> import numpy as np
Предположим, у нас есть плотность:
\[\begin{split}f(x) = \begin{cases} 1 - x^2, & -1 \leq x \leq 1 \\ 0, & \text{otherwise} \end{cases}\end{split}\]Производная этой функции плотности:
\[\begin{split}\frac{df(x)}{dx} = \begin{cases} -2x, & -1 \leq x \leq 1 \\ 0, & \text{otherwise} \end{cases}\end{split}\]Обратите внимание, что PDF не интегрируется в 1. Поскольку это метод, основанный на отбраковке, нам не нужна нормированная PDF. Для инициализации генератора мы можем использовать:
>>> urng = np.random.default_rng() >>> class MyDist: ... def pdf(self, x): ... return 1-x*x ... def dpdf(self, x): ... return -2*x ... >>> dist = MyDist() >>> rng = TransformedDensityRejection(dist, domain=(-1, 1), ... random_state=urng)
Область определения может быть очень полезной для усечения распределения, но чтобы избежать передачи её каждый раз в конструктор, область определения по умолчанию может быть установлена путем предоставления поддержка метод в объекте распределения (dist):
>>> class MyDist: ... def pdf(self, x): ... return 1-x*x ... def dpdf(self, x): ... return -2*x ... def support(self): ... return (-1, 1) ... >>> dist = MyDist() >>> rng = TransformedDensityRejection(dist, random_state=urng)
Теперь мы можем использовать
rvsметод для генерации выборок из распределения:>>> rvs = rng.rvs(1000)
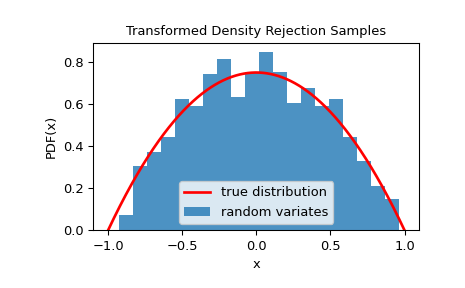
Мы можем проверить, что выборки взяты из заданного распределения, визуализировав его гистограмму:
>>> import matplotlib.pyplot as plt >>> x = np.linspace(-1, 1, 1000) >>> fx = 3/4 * dist.pdf(x) # 3/4 is the normalizing constant >>> plt.plot(x, fx, 'r-', lw=2, label='true distribution') >>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates') >>> plt.xlabel('x') >>> plt.ylabel('PDF(x)') >>> plt.title('Transformed Density Rejection Samples') >>> plt.legend() >>> plt.show()