scipy.cluster.vq.

kmeans2

scipy.cluster.vq.kmeans2(данные, k, iter=10, порог=1e-05, minit='random', missing='warn', check_finite=True, *, rng=None, seed=None)

Классифицирует набор наблюдений в k кластеров с использованием алгоритма k-средних.

Алгоритм пытается минимизировать евклидово расстояние между наблюдениями и центроидами. Включено несколько методов инициализации.

Параметры:

данныеndarray

Массив 'M' на 'N' из 'M' наблюдений в 'N' измерениях или массив длины 'M' из 'M' одномерных наблюдений.

kint или ndarray

Количество кластеров для формирования, а также количество центроидов для генерации. Если minit строка инициализации ‘matrix’, или если вместо этого задан ndarray, он интерпретируется как начальный кластер для использования.

iterint, необязательный

Количество итераций алгоритма k-средних для выполнения. Обратите внимание, что это отличается по смыслу от параметра iters функции kmeans.

порогfloat, опционально

(еще не используется)

minitstr, optional

Метод инициализации. Доступные методы: ‘random’, ‘points’, ‘++’ и ‘matrix’:

‘random’: сгенерировать k центроидов из гауссовского распределения со средним и дисперсией, оценёнными по данным.

'points': выбрать k наблюдений (строк) случайным образом из данных для начальных центроидов.

‘++’: выбрать k наблюдений в соответствии с методом kmeans++ (аккуратная инициализация)

'matrix': интерпретировать параметр k как массив k на M (или массив длины k для 1-D данных) начальных центроидов.

missingstr, optional

Метод обработки пустых кластеров. Доступные методы: ‘warn’ и ‘raise’:

'warn': выдать предупреждение и продолжить.

‘raise’: вызвать ClusterError и завершить алгоритм.

check_finitebool, необязательно

Проверять ли, что входные матрицы содержат только конечные числа. Отключение может дать прирост производительности, но может привести к проблемам (сбои, незавершение) если входные данные содержат бесконечности или NaN. По умолчанию: True

rng{None, int, numpy.random.Generator, опционально

Если rng передается по ключевому слову, типы, отличные от numpy.random.Generator передаются в numpy.random.default_rng для создания экземпляра Generator. Если rng уже является Generator экземпляр, то предоставленный экземпляр используется. Укажите rng для повторяемого поведения функции.

Если этот аргумент передаётся по позиции или seed передается по ключевому слову, устаревшее поведение для аргумента seed применяется:

• Если seed равно None (или numpy.random), numpy.random.RandomState используется синглтон.

• Если seed является int, новый RandomState используется экземпляр, инициализированный с seed.

• Если seed уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Изменено в версии 1.15.0: В рамках SPEC-007 переход от использования numpy.random.RandomState to numpy.random.Generator, этот ключевое слово было изменено с seed to rng. В переходный период оба ключевых слова будут продолжать работать, хотя только одно может быть указано за раз. После переходного периода вызовы функций, использующие seed ключевое слово будет выдавать предупреждения. Поведение обоих seed и rng описаны выше, но только rng ключевое слово должно использоваться в новом коде.

Возвращает:

центроидndarray

Массив центроидов размером ‘k’ на ‘N’, найденных на последней итерации k-средних.

меткаndarray

label[i] - это код или индекс центроида, к которому ближе всего i-е наблюдение.

Смотрите также

kmeans

Примечания

kmeans2 имеет экспериментальную поддержку совместимых с Python Array API Standard бэкендов в дополнение к NumPy. Пожалуйста, рассмотрите тестирование этих функций, установив переменную окружения SCIPY_ARRAY_API=1 и предоставление массивов CuPy, PyTorch, JAX или Dask в качестве аргументов массива. Поддерживаются следующие комбинации бэкенда и устройства (или других возможностей).

Библиотека	CPU	GPU
NumPy	✅	н/д
CuPy	н/д	⛔
PyTorch	✅	⛔
JAX	⚠️ нет JIT	⛔
Dask	⚠️ вычисляет граф	н/д

См. Поддержка стандарта array API для получения дополнительной информации.

Ссылки

[1]

Д. Артур и С. Васильвицкий, "k-means++: преимущества тщательного начального выбора", Труды Восемнадцатого Ежегодного Симпозиума ACM-SIAM по Дискретным Алгоритмам, 2007.

Примеры

Попробуйте в вашем браузере!

>>> from scipy.cluster.vq import kmeans2
>>> import matplotlib.pyplot as plt
>>> import numpy as np

Создайте z, массив формы (100, 2), содержащий смесь выборок из трёх многомерных нормальных распределений.

>>> rng = np.random.default_rng()
>>> a = rng.multivariate_normal([0, 6], [[2, 1], [1, 1.5]], size=45)
>>> b = rng.multivariate_normal([2, 0], [[1, -1], [-1, 3]], size=30)
>>> c = rng.multivariate_normal([6, 4], [[5, 0], [0, 1.2]], size=25)
>>> z = np.concatenate((a, b, c))
>>> rng.shuffle(z)

Вычислить три кластера.

>>> centroid, label = kmeans2(z, 3, minit='points')
>>> centroid
array([[ 2.22274463, -0.61666946],  # may vary
       [ 0.54069047,  5.86541444],
       [ 6.73846769,  4.01991898]])

Сколько точек в каждом кластере?

>>> counts = np.bincount(label)
>>> counts
array([29, 51, 20])  # may vary

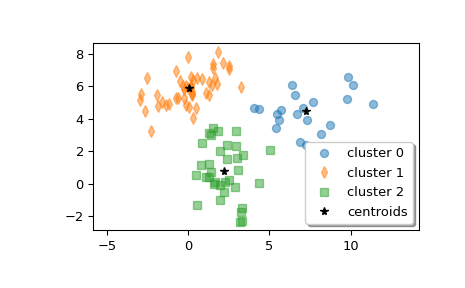
Построить кластеры.

>>> w0 = z[label == 0]
>>> w1 = z[label == 1]
>>> w2 = z[label == 2]
>>> plt.plot(w0[:, 0], w0[:, 1], 'o', alpha=0.5, label='cluster 0')
>>> plt.plot(w1[:, 0], w1[:, 1], 'd', alpha=0.5, label='cluster 1')
>>> plt.plot(w2[:, 0], w2[:, 1], 's', alpha=0.5, label='cluster 2')
>>> plt.plot(centroid[:, 0], centroid[:, 1], 'k*', label='centroids')
>>> plt.axis('equal')
>>> plt.legend(shadow=True)
>>> plt.show()

НазадОткрыть во вкладке