scipy.fft.

fht#

scipy.fft.fht(a, dln, mu, смещение=0.0, смещение=0.0)[источник]#

Вычислить быстрое преобразование Ханкеля.

Вычисляет дискретное преобразование Ханкеля логарифмически равномерной периодической последовательности с использованием алгоритма FFTLog [1], [2].

Параметры:

aarray_like (…, n): Вещественный периодический входной массив, равномерно логарифмически распределенный. Для многомерного входа преобразование выполняется по последней оси.
dlnfloat: Равномерное логарифмическое распределение входного массива.
mufloat: Порядок преобразования Ханкеля, любое положительное или отрицательное вещественное число.
смещениеfloat, опционально: Смещение равномерного логарифмического интервала выходного массива.
смещениеfloat, опционально: Показатель степенного закона смещения, любое положительное или отрицательное вещественное число.

Возвращает:

Aarray_like (…, n): Преобразованный выходной массив, который является вещественным, периодическим, равномерно логарифмически распределённым и имеет ту же форму, что и входной массив.

Смотрите также

ifht: Обратная величина fht.
fhtoffset: Возвращает оптимальное смещение для fht.

Примечания

Эта функция вычисляет дискретную версию преобразования Ханкеля

\[A(k) = \int_{0}^{\infty} \! a(r) \, J_\mu(kr) \, k \, dr \;,\]

где \(J_\mu\) является функцией Бесселя порядка \(\mu\). Индекс \(\mu\) может быть любым действительным числом, положительным или отрицательным. Обратите внимание, что численное преобразование Ханкеля использует подынтегральное выражение вида \(k \, dr\), в то время как математическое преобразование Ханкеля обычно определяется с использованием \(r \, dr\).

Входной массив a является периодической последовательностью длины \(n\), равномерно логарифмически распределенные с шагом dln,

\[a_j = a(r_j) \;, \quad r_j = r_c \exp[(j-j_c) \, \mathtt{dln}]\]

с центром в точке \(r_c\). Обратите внимание, что центральный индекс \(j_c = (n-1)/2\) является полуцелым, если \(n\) является чётным, так что \(r_c\) находится между двумя входными элементами. Аналогично, выходной массив A является периодической последовательностью длины \(n\), также равномерно логарифмически распределенные с шагом dln

\[A_j = A(k_j) \;, \quad k_j = k_c \exp[(j-j_c) \, \mathtt{dln}]\]

с центром в точке \(k_c\).

Центральные точки \(r_c\) и \(k_c\) периодических интервалов может быть выбрано произвольно, но обычно выбирают произведение \(k_c r_c = k_j r_{n-1-j} = k_{n-1-j} r_j\) равной единице. Это можно изменить с помощью смещение параметр, который управляет логарифмическим смещением \(\log(k_c) = \mathtt{offset} - \log(r_c)\) выходного массива. Выбор оптимального значения для смещение может уменьшить звон дискретного преобразования Ханкеля.

Если смещение параметр ненулевой, эта функция вычисляет дискретную версию смещённого преобразования Ханкеля

\[A(k) = \int_{0}^{\infty} \! a_q(r) \, (kr)^q \, J_\mu(kr) \, k \, dr\]

где \(q\) является значением смещение, и степенной закон смещения \(a_q(r) = a(r) \, (kr)^{-q}\) применяется к входной последовательности. Смещение преобразования может помочь аппроксимировать непрерывное преобразование \(a(r)\) если существует значение \(q\) такой, что \(a_q(r)\) близка к периодической последовательности, в этом случае результирующая \(A(k)\) будет близок к непрерывному преобразованию.

Ссылки

[1]

Talman J. D., 1978, J. Comp. Phys., 29, 35

[2] (1,2)

Hamilton A. J. S., 2000, MNRAS, 312, 257 (astro-ph/9905191)

Примеры

Этот пример является адаптированной версией fftlogtest.f который предоставляется в [2]. Он вычисляет интеграл

\[\int^\infty_0 r^{\mu+1} \exp(-r^2/2) J_\mu(kr) k dr = k^{\mu+1} \exp(-k^2/2) .\]

>>> import numpy as np
>>> from scipy import fft
>>> import matplotlib.pyplot as plt

Параметры преобразования.

>>> mu = 0.0                     # Order mu of Bessel function
>>> r = np.logspace(-7, 1, 128)  # Input evaluation points
>>> dln = np.log(r[1]/r[0])      # Step size
>>> offset = fft.fhtoffset(dln, initial=-6*np.log(10), mu=mu)
>>> k = np.exp(offset)/r[::-1]   # Output evaluation points

Определите аналитическую функцию.

>>> def f(x, mu):
...     """Analytical function: x^(mu+1) exp(-x^2/2)."""
...     return x**(mu + 1)*np.exp(-x**2/2)

Вычислить функцию в r и вычислить соответствующие значения в k используя FFTLog.

>>> a_r = f(r, mu)
>>> fht = fft.fht(a_r, dln, mu=mu, offset=offset)

Для этого примера мы можем фактически вычислить аналитический отклик (который в данном случае совпадает с входной функцией) для сравнения и вычислить относительную ошибку.

>>> a_k = f(k, mu)
>>> rel_err = abs((fht-a_k)/a_k)

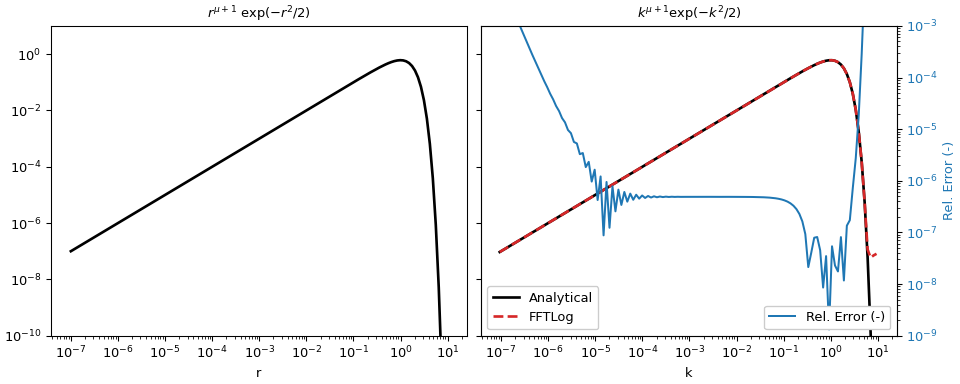
Построить результат.

>>> figargs = {'sharex': True, 'sharey': True, 'constrained_layout': True}
>>> fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4), **figargs)
>>> ax1.set_title(r'$r^{\mu+1}\ \exp(-r^2/2)$')
>>> ax1.loglog(r, a_r, 'k', lw=2)
>>> ax1.set_xlabel('r')
>>> ax2.set_title(r'$k^{\mu+1} \exp(-k^2/2)$')
>>> ax2.loglog(k, a_k, 'k', lw=2, label='Analytical')
>>> ax2.loglog(k, fht, 'C3--', lw=2, label='FFTLog')
>>> ax2.set_xlabel('k')
>>> ax2.legend(loc=3, framealpha=1)
>>> ax2.set_ylim([1e-10, 1e1])
>>> ax2b = ax2.twinx()
>>> ax2b.loglog(k, rel_err, 'C0', label='Rel. Error (-)')
>>> ax2b.set_ylabel('Rel. Error (-)', color='C0')
>>> ax2b.tick_params(axis='y', labelcolor='C0')
>>> ax2b.legend(loc=4, framealpha=1)
>>> ax2b.set_ylim([1e-9, 1e-3])
>>> plt.show()