scipy.integrate.

lebedev_rule#

scipy.integrate.lebedev_rule(n)[источник]#

Квадратура Лебедева.

Вычисление точек выборки и весов для квадратуры Лебедева [1] для интегрирования функции по поверхности единичной сферы.

Параметры:

nint: Порядок квадратуры. См. Notes для поддерживаемых значений.

Возвращает:

xndarray формы (3, m): Точки выборки на единичной сфере в декартовых координатах. m это «степень», соответствующая указанному порядку; см. Примечания.
wndarray формы (m,): Веса

Примечания

Реализовано путём перевода кода Matlab из [2] в Python.

Доступные порядки (аргумент n) являются:

3, 5, 7, 9, 11, 13, 15, 17,
19, 21, 23, 25, 27, 29, 31, 35,
41, 47, 53, 59, 65, 71, 77, 83,
89, 95, 101, 107, 113, 119, 125, 131

Соответствующие степени m являются:

6, 14, 26, 38, 50, 74, 86, 110,
146, 170, 194, 230, 266, 302, 350, 434,
590, 770, 974, 1202, 1454, 1730, 2030, 2354,
2702, 3074, 3470, 3890, 4334, 4802, 5294, 5810

Ссылки

[1]

В.И. Лебедев и Д.Н. Лайков. «Квадратурная формула для сферы 131-го алгебраического порядка точности». Доклады математики, Том 59, № 3, 1999, стр. 477-481.

[2]

R. Parrish. getLebedevSphere. Matlab Central File Exchange. https://www.mathworks.com/matlabcentral/fileexchange/27097-getlebedevsphere.

[3]

Bellet, Jean-Baptiste, Matthieu Brachet, and Jean-Pierre Croisille. “Quadrature and symmetry on the Cubed Sphere.” Journal of Computational and Applied Mathematics 409 (2022): 114142. DOI:10.1016/j.cam.2022.114142.

Примеры

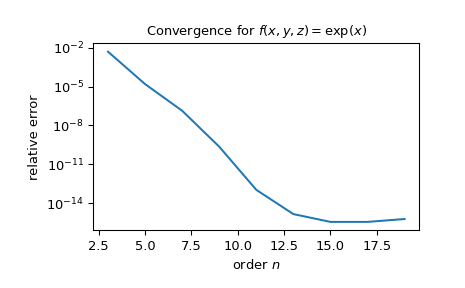
Пример, приведённый в [3] является интегрированием \(f(x, y, z) = \exp(x)\) по сфере радиуса \(1\); ссылка на это находится 14.7680137457653. Показать сходимость к ожидаемому результату по мере увеличения порядка:

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.integrate import lebedev_rule
>>>
>>> def f(x):
...     return np.exp(x[0])
>>>
>>> res = []
>>> orders = np.arange(3, 20, 2)
>>> for n in orders:
...     x, w = lebedev_rule(n)
...     res.append(w @ f(x))
>>>
>>> ref = np.full_like(res, 14.7680137457653)
>>> err = abs(res - ref)/abs(ref)
>>> plt.semilogy(orders, err)
>>> plt.xlabel('order $n$')
>>> plt.ylabel('relative error')
>>> plt.title(r'Convergence for $f(x, y, z) = \exp(x)$')
>>> plt.show()

../../_images/scipy-integrate-lebedev_rule-1.png