scipy.integrate.

odeint

scipy.integrate.odeint(функция, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)

Интегрировать систему обыкновенных дифференциальных уравнений.

Примечание

Для нового кода используйте scipy.integrate.solve_ivp для решения дифференциального уравнения.

Решить систему обыкновенных дифференциальных уравнений с использованием lsoda из библиотеки FORTRAN odepack.

Решает задачу Коши для жестких или нежестких систем обыкновенных дифференциальных уравнений первого порядка:

dy/dt = func(y, t, ...)  [or func(t, y, ...)]

где y может быть вектором.

Примечание

По умолчанию, требуемый порядок первых двух аргументов функция идут в обратном порядке аргументов в функции определения системы, используемой scipy.integrate.ode класс и функция scipy.integrate.solve_ivp. Чтобы использовать функцию с сигнатурой func(t, y, ...), аргумент tfirst должно быть установлено в True.

Параметры:

функциявызываемый(y, t, …) или вызываемый(t, y, …)

Вычисляет производную y в точке t. Если сигнатура callable(t, y, ...), тогда аргумент tfirst должен быть установлен True. функция не должен изменять данные в y, так как это представление данных, используемых внутри решателя ОДУ.

y0массив

Начальное условие на y (может быть вектором).

tмассив

Последовательность временных точек, для которых решается y. Начальная точка значения должна быть первым элементом этой последовательности. Эта последовательность должна быть монотонно возрастающей или монотонно убывающей; повторяющиеся значения допускаются.

argsкортеж, необязательный

Дополнительные аргументы для передачи в функцию.

Dfunвызываемый(y, t, …) или вызываемый(t, y, …)

Градиент (якобиан) от функция. Если сигнатура callable(t, y, ...), тогда аргумент tfirst должен быть установлен True. Dfun не должен изменять данные в y, так как это представление данных, используемых внутри решателя ОДУ.

col_derivbool, необязательно

True, если Dfun определяет производные по столбцам (быстрее), иначе Dfun должен определять производные по строкам.

full_outputbool, необязательно

True, если нужно вернуть словарь дополнительных выходных данных как второй выход

printmessgbool, необязательно

Выводить ли сообщение о сходимости

tfirstbool, необязательно

Если True, первые два аргумента функция (и Dfun, если задано) должен t, y вместо значения по умолчанию y, t.

Добавлено в версии 1.1.0.

Возвращает:

yмассив, форма (len(t), len(y0))

Массив, содержащий значение y для каждого желаемого времени в t, с начальным значением y0 в первой строке.

infodictdict, возвращается только если full_output == True

Словарь, содержащий дополнительную выходную информацию

ключ	значение
'hu'	вектор размеров шагов, успешно использованных для каждого временного шага
‘tcur’	вектор со значением t, достигнутым на каждом временном шаге (всегда будет не меньше входных времен)
‘tolsf’	вектор масштабных коэффициентов допуска, больше 1.0, вычисляется при обнаружении запроса на слишком высокую точность
‘tsw’	значение t в момент последнего переключения метода (указано для каждого временного шага)
‘nst’	кумулятивное количество временных шагов
‘nfe’	кумулятивное количество вычислений функции для каждого временного шага
‘nje’	кумулятивное количество вычислений якобиана для каждого временного шага
'nqu'	вектор порядков метода для каждого успешного шага
‘imxer’	индекс компоненты наибольшей величины в взвешенном векторе локальной ошибки (e / ewt) при возврате ошибки, -1 в противном случае
'lenrw'	длина требуемого двойного рабочего массива
‘leniw’	длина требуемого целочисленного рабочего массива
‘mused’	вектор индикаторов метода для каждого успешного шага по времени: 1: adams (нежесткий), 2: bdf (жесткий)

Другие параметры:

ml, muint, необязательный

Если любой из этих параметров не равен None или неотрицателен, то предполагается, что матрица Якоби является ленточной. Эти параметры задают количество нижних и верхних ненулевых диагоналей в этой ленточной матрице. Для ленточного случая, Dfun должна возвращать матрицу, строки которой содержат ненулевые диагонали (начиная с самой нижней). Таким образом, возвращаемая матрица jac из Dfun должен иметь форму (ml + mu + 1, len(y0)) когда ml >=0 или mu >=0. Данные в jac должны храниться так, чтобы jac[i - j + mu, j] содержит производную от i-го уравнения относительно jth переменная состояния. Если col_deriv если True, транспонирование этого jac должны быть возвращены.

rtol, atolfloat, опционально

Входные параметры rtol и atol определить контроль ошибки, выполняемый решателем. Решатель будет контролировать вектор, e, оцененных локальных ошибок в y, согласно неравенству вида max-norm of (e / ewt) <= 1, где ewt — вектор положительных весов ошибок, вычисляемый как ewt = rtol * abs(y) + atol. rtol и atol могут быть либо векторами той же длины, что и y, либо скалярами. По умолчанию 1.49012e-8.

tcritndarray, необязательно

Вектор критических точек (например, сингулярностей), где следует проявлять осторожность при интегрировании.

h0float, (0: определяется решателем), опционально

Шаг, который будет предпринят на первом шаге.

hmaxfloat, (0: определяется решателем), опционально

Максимально допустимый абсолютный размер шага.

hminfloat, (0: определяется решателем), опционально

Минимально допустимый абсолютный размер шага.

ixprbool, необязательно

Следует ли генерировать дополнительную печать при переключении методов.

mxstepint, (0: определяется решателем), опционально

Максимальное количество (внутренне определенных) шагов, разрешенных для каждой точки интегрирования в t.

mxhnilint, (0: определяется решателем), опционально

Максимальное количество выводимых сообщений.

mxordnint, (0: определяется решателем), опционально

Максимальный порядок, разрешённый для нежёсткого (Адамса) метода.

mxordsint, (0: определяется решателем), опционально

Максимальный порядок, разрешённый для жёсткого (BDF) метода.

Смотрите также

solve_ivp

решить задачу Коши для системы ОДУ

ode

более объектно-ориентированный интегратор на основе VODE

quad

для нахождения площади под кривой

Примеры

Попробуйте в вашем браузере!

Дифференциальное уравнение второго порядка для угла theta маятника, на который действует гравитация с трением, может быть записано:

theta''(t) + b*theta'(t) + c*sin(theta(t)) = 0

где b и c являются положительными константами, а штрих (’) обозначает производную. Чтобы решить это уравнение с помощью odeint, мы должны сначала преобразовать его в систему уравнений первого порядка. Определяя угловую скорость omega(t) = theta'(t), получаем систему:

theta'(t) = omega(t)
omega'(t) = -b*omega(t) - c*sin(theta(t))

Пусть y будет вектором [theta, omega]. Мы реализуем эту систему в Python как:

>>> import numpy as np
>>> def pend(y, t, b, c):
...     theta, omega = y
...     dydt = [omega, -b*omega - c*np.sin(theta)]
...     return dydt
...

Мы предполагаем, что константы равны b = 0.25 и c = 5.0:

>>> b = 0.25
>>> c = 5.0

Для начальных условий предполагаем, что маятник почти вертикален с theta(0) = pi - 0.1 и изначально находится в покое, так что omega(0) = 0. Тогда вектор начальных условий равен

>>> y0 = [np.pi - 0.1, 0.0]

Мы сгенерируем решение в 101 равномерно распределенных точках на интервале 0 <= t <= 10. Таким образом, наш массив времен:

>>> t = np.linspace(0, 10, 101)

Вызов odeint для генерации решения. Чтобы передать параметры b и c to pend, мы передаём их odeint используя args аргумент.

>>> from scipy.integrate import odeint
>>> sol = odeint(pend, y0, t, args=(b, c))

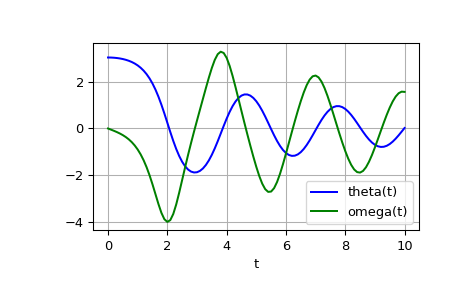
Решение представляет собой массив формы (101, 2). Первый столбец — это theta(t), а второй - omega(t). Следующий код строит графики обеих компонент.

>>> import matplotlib.pyplot as plt
>>> plt.plot(t, sol[:, 0], 'b', label='theta(t)')
>>> plt.plot(t, sol[:, 1], 'g', label='omega(t)')
>>> plt.legend(loc='best')
>>> plt.xlabel('t')
>>> plt.grid()
>>> plt.show()

НазадОткрыть во вкладке