scipy.integrate.

solve_ivp

scipy.integrate.solve_ivp(fun, t_span, y0, метод='RK45', t_eval=None, dense_output=False, события=None, векторизованный=False, args=None, **опции)

Решите задачу Коши для системы ОДУ.

Эта функция численно интегрирует систему обыкновенных дифференциальных уравнений при заданном начальном значении:

dy / dt = f(t, y)
y(t0) = y0

Здесь t — независимая переменная 1-D (время), y(t) — векторная функция N-D (состояние), а векторная функция N-D f(t, y) определяет дифференциальные уравнения. Цель — найти y(t), приближенно удовлетворяющую дифференциальным уравнениям, при заданном начальном значении y(t0)=y0.

Некоторые решатели поддерживают интегрирование в комплексной области, но обратите внимание, что для жестких решателей ОДУ правая часть должна быть комплексно-дифференцируемой (удовлетворять уравнениям Коши-Римана [11]). Чтобы решить задачу в комплексной области, передайте y0 с комплексным типом данных. Другой всегда доступный вариант — переписать вашу задачу отдельно для действительной и мнимой частей.

Параметры:

funcallable

Правая часть системы: производная состояния по времени y в момент t. Сигнатура вызова: fun(t, y), где t является скаляром и y является ndarray с len(y) = len(y0). Дополнительные аргументы необходимо передать, если args используется (см. документацию args аргумент). fun должен возвращать массив той же формы, что и y. См. векторизованный для получения дополнительной информации.

t_spanпоследовательность из 2 элементов

Интервал интегрирования (t0, tf). Решатель начинает с t=t0 и интегрирует до достижения t=tf. И t0, и tf должны быть числами с плавающей запятой или значениями, интерпретируемыми функцией преобразования в float.

y0array_like, форма (n,)

Начальное состояние. Для задач в комплексной области передайте y0 с комплексным типом данных (даже если начальное значение чисто вещественное).

методстрока или OdeSolver, опционально

Метод интегрирования для использования:

• ‘RK45’ (по умолчанию): Явный метод Рунге-Кутты порядка 5(4) [1]. Ошибка контролируется с учётом точности метода четвёртого порядка, но шаги выполняются с использованием формулы пятого порядка (выполняется локальная экстраполяция). Для плотного вывода используется интерполяционный полином четвёртой степени [2]. Может применяться в комплексной области.

• ‘RK23’: Явный метод Рунге-Кутты порядка 3(2) [3]. Погрешность контролируется в предположении точности метода второго порядка, но шаги выполняются с использованием формулы третьего порядка (выполняется локальная экстраполяция). Для плотного вывода используется кубический полином Эрмита. Может применяться в комплексной области.

• 'DOP853': Явный метод Рунге-Кутты 8-го порядка [13]. Реализация алгоритма “DOP853” на Python, изначально написанного на Fortran [14]. Для плотного вывода используется интерполяционный полином 7-го порядка, точный до 7-го порядка. Может применяться в комплексной области.

• 'Radau': Неявный метод Рунге-Кутты семейства Radau IIA порядка 5 [4]. Ошибка контролируется с помощью встроенной формулы третьего порядка точности. Для плотного вывода используется кубический полином, удовлетворяющий условиям коллокации.

• 'BDF': Неявный многошаговый метод переменного порядка (от 1 до 5), основанный на формуле обратного дифференцирования для аппроксимации производной [5]. Реализация следует описанию в [6]. Используется квазипостоянная схема шага, и точность повышается с помощью модификации NDF. Может применяться в комплексной области.

• ‘LSODA’: метод Адамса/BDF с автоматическим определением жесткости и переключением [7], [8]. Это обёртка решателя Fortran из ODEPACK.

Явные методы Рунге-Кутты (‘RK23’, ‘RK45’, ‘DOP853’) следует использовать для нежестких задач, а неявные методы (‘Radau’, ‘BDF’) для жестких задач [9]. Среди методов Рунге-Кутты 'DOP853' рекомендуется для решения с высокой точностью (низкие значения rtol и atol).

Если не уверены, сначала попробуйте запустить 'RK45'. Если он выполняет необычно много итераций, расходится или завершается с ошибкой, ваша проблема, вероятно, является жесткой, и вам следует использовать 'Radau' или 'BDF'. 'LSODA' также может быть хорошим универсальным выбором, но с ним может быть несколько менее удобно работать, так как он оборачивает старый код на Fortran.

Вы также можете передать произвольный класс, производный от OdeSolver который реализует решатель.

t_evalarray_like или None, необязательный

Времена, в которые сохраняется вычисленное решение, должны быть отсортированы и лежать в пределах t_spanЕсли None (по умолчанию), используются точки, выбранные решателем.

dense_outputbool, необязательно

Определяет, вычислять ли непрерывное решение. По умолчанию False.

событиявызываемый объект или список вызываемых объектов, опционально

События для отслеживания. Если None (по умолчанию), события отслеживаться не будут. Каждое событие происходит в нулях непрерывной функции времени и состояния. Каждая функция должна иметь сигнатуру event(t, y) где дополнительные аргументы должны быть переданы, если args используется (см. документацию args аргумент). Каждая функция должна возвращать float. Решатель найдет точное значение t в котором event(t, y(t)) = 0 используя алгоритм нахождения корней. По умолчанию будут найдены все нули. Решатель ищет смену знака на каждом шаге, поэтому если несколько пересечений нуля происходят в пределах одного шага, события могут быть пропущены. Кроме того, каждый событие Функция может иметь следующие атрибуты:

terminal: bool или int, опционально

Если логическое значение, указывает, следует ли завершать интегрирование при возникновении этого события. Если целочисленное, завершение происходит после указанного количества возникновений этого события. Неявно False, если не назначено.

direction: float, optional

Направление пересечения нуля. Если направление положительно, событие будет срабатывать только при переходе от отрицательного к положительному, и наоборот, если направление отрицательно. Если 0, то любое направление вызовет событие. Неявно 0, если не назначено.

Вы можете назначать атрибуты, такие как event.terminal = True любой функции в Python.

векторизованныйbool, необязательно

Определяет ли fun может вызываться векторизованно. По умолчанию False.

Если vectorized равно False, fun всегда будет вызываться с y формы (n,), где n = len(y0).

Если vectorized равно True, fun может вызываться с y формы (n, k), где k является целым числом. В этом случае, fun должен вести себя таким образом, что fun(t, y)[:, i] == fun(t, y[:, i]) (т.е. каждый столбец возвращаемого массива является производной по времени состояния, соответствующего столбцу y).

Установка vectorized=True позволяет быстрее аппроксимировать якобиан методом конечных разностей методами 'Radau' и 'BDF', но приведет к более медленному выполнению для других методов и для 'Radau' и 'BDF' в некоторых случаях (например, малый len(y0)).

argsкортеж, необязательный

Дополнительные аргументы для передачи пользовательским функциям. Если заданы, дополнительные аргументы передаются всем пользовательским функциям. Так что если, например, fun имеет сигнатуру fun(t, y, a, b, c), затем jac (если заданы) и любые функции событий должны иметь ту же сигнатуру, и args должен быть кортежем длины 3.

**options

Параметры, передаваемые выбранному решателю. Все доступные параметры для уже реализованных решателей перечислены ниже.

first_stepfloat или None, опционально

Начальный размер шага. По умолчанию None что означает, что алгоритм должен выбрать.

max_stepfloat, опционально

Максимально допустимый размер шага. По умолчанию np.inf, т.е. размер шага не ограничен и определяется исключительно решателем.

rtol, atolfloat или array_like, опционально

Относительные и абсолютные допуски. Решатель поддерживает оценки локальной ошибки меньше, чем atol + rtol * abs(y). Здесь rtol управляет относительной точностью (количеством верных цифр), в то время как atol управляет абсолютной точностью (количество верных десятичных знаков). Для достижения желаемой rtol, установите atol быть меньше наименьшего значения, которое можно ожидать от rtol * abs(y) так что rtol доминирует над допустимой ошибкой. Если atol больше, чем rtol * abs(y) количество верных цифр не гарантируется. И наоборот, для достижения желаемого atol set rtol такой, что rtol * abs(y) всегда меньше чем atol. Если компоненты y имеют разные масштабы, может быть полезно установить разные atol значения для различных компонентов, передавая array_like с формой (n,) для atol. Значения по умолчанию: 1e-3 для rtol и 1e-6 для atol.

jacarray_like, sparse_matrix, callable или None, опционально

Матрица Якоби правой части системы по отношению к y, требуемая методами 'Radau', 'BDF' и 'LSODA'. Матрица Якоби имеет форму (n, n), и её элемент (i, j) равен d f_i / d y_j. Существует три способа определения якобиана:

• Если array_like или sparse_matrix, предполагается, что якобиан постоянен. Не поддерживается 'LSODA'.

• Если вызываемый объект, предполагается, что якобиан зависит от обоих t и y; он будет вызван как jac(t, y), по мере необходимости. Дополнительные аргументы должны быть переданы, если args используется (см. документацию args аргумент). Для методов 'Radau' и 'BDF' возвращаемое значение может быть разреженной матрицей.

• Если None (по умолчанию), Якобиан будет аппроксимирован конечными разностями.

Обычно рекомендуется предоставлять Якобиан, а не полагаться на аппроксимацию конечными разностями.

jac_sparsityarray_like, sparse matrix или None, опционально

Определяет структуру разреженности матрицы Якоби для аппроксимации конечными разностями. Её форма должна быть (n, n). Этот аргумент игнорируется, если jac не является None. Если якобиан имеет только несколько ненулевых элементов в каждый строка, предоставление структуры разреженности значительно ускорит вычисления [10]. Нулевой элемент означает, что соответствующий элемент в матрице Якоби всегда равен нулю. Если None (по умолчанию), матрица Якоби считается плотной. Не поддерживается 'LSODA', см. lband и uband вместо этого.

lband, ubandint или None, опционально

Параметры, определяющие ширину полосы Якобиана для метода 'LSODA', т.е., jac[i, j] != 0 only for i - lband <= j <= i + uband. По умолчанию None. Установка этих параметров требует, чтобы ваша jac-функция возвращала якобиан в упакованном формате: возвращаемый массив должен иметь n столбцы и uband + lband + 1 строки, в которые записываются диагонали Якобиана. В частности jac_packed[uband + i - j , j] = jac[i, j]. Тот же формат используется в scipy.linalg.solve_banded (см. иллюстрацию). Эти параметры также могут использоваться с jac=None для уменьшения количества элементов матрицы Якоби, оцениваемых методом конечных разностей.

min_stepfloat, опционально

Минимально допустимый размер шага для метода ‘LSODA’. По умолчанию min_step равно нулю.

Возвращает:

Объект Bunch со следующими определёнными полями:

tndarray, форма (n_points,)

Временные точки.

yndarray, форма (n, n_points)

Значения решения в t.

solOdeSolution или None

Решение найдено как OdeSolution экземпляр; None, если dense_output был установлен в False.

t_eventsсписок ndarray или None

Содержит для каждого типа события список массивов, в которых событие этого типа было обнаружено. None, если события был None.

y_eventsсписок ndarray или None

Для каждого значения t_events, соответствующее значение решения. None, если события был None.

nfevint

Количество вычислений правой части.

njevint

Количество вычислений якобиана.

nluint

Количество LU-разложений.

statusint

Причина завершения алгоритма:

• -1: Шаг интегрирования не выполнен.

• 0: Решатель успешно достиг конца tspan.

• 1: Произошло событие завершения.

messagestring

Человекочитаемое описание причины завершения.

successbool

True, если решатель достиг конца интервала или произошло событие завершения (status >= 0).

Ссылки

[1]

J. R. Dormand, P. J. Prince, "Семейство вложенных формул Рунге-Кутты", Журнал вычислительной и прикладной математики, Том 6, № 1, стр. 19-26, 1980.

[2]

L. W. Shampine, «Some Practical Runge-Kutta Formulas», Mathematics of Computation, Vol. 46, No. 173, pp. 135-150, 1986.

[3]

П. Богацкий, Л.Ф. Шампин, "Пара формул Рунге-Кутты 3(2)", Appl. Math. Lett. Том 2, № 4. стр. 321-325, 1989.

[4]

E. Hairer, G. Wanner, "Решение обыкновенных дифференциальных уравнений II: Жесткие и дифференциально-алгебраические задачи", разд. IV.8.

[5]

Формула обратного дифференцирования в Википедии.

[6]

L. F. Shampine, M. W. Reichelt, "THE MATLAB ODE SUITE", SIAM J. SCI. COMPUTE., Vol. 18, No. 1, pp. 1-22, January 1997.

[7]

A. C. Hindmarsh, "ODEPACK, A Systematized Collection of ODE Solvers," IMACS Transactions on Scientific Computation, Vol 1., pp. 55-64, 1983.

[8]

L. Petzold, “Автоматический выбор методов решения жестких и нежестких систем обыкновенных дифференциальных уравнений”, SIAM Journal on Scientific and Statistical Computing, Vol. 4, No. 1, pp. 136-148, 1983.

[9]

Жёсткое уравнение на Википедии.

[10]

A. Curtis, M. J. D. Powell, и J. Reid, “On the estimation of sparse Jacobian matrices”, Journal of the Institute of Mathematics and its Applications, 13, pp. 117-120, 1974.

[11]

уравнения Коши-Римана на Википедии.

[12]

Уравнения Лотки-Вольтерры в Википедии.

[13]

E. Hairer, S. P. Norsett G. Wanner, «Решение обыкновенных дифференциальных уравнений I: Нежесткие задачи», разд. II.

[14]

Страница с исходным кодом Fortran DOP853.

Примеры

Попробуйте в вашем браузере!

Базовое экспоненциальное затухание с автоматически выбранными временными точками.

>>> import numpy as np
>>> from scipy.integrate import solve_ivp
>>> def exponential_decay(t, y): return -0.5 * y
>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8])
>>> print(sol.t)
[ 0.          0.11487653  1.26364188  3.06061781  4.81611105  6.57445806
  8.33328988 10.        ]
>>> print(sol.y)
[[2.         1.88836035 1.06327177 0.43319312 0.18017253 0.07483045
  0.03107158 0.01350781]
 [4.         3.7767207  2.12654355 0.86638624 0.36034507 0.14966091
  0.06214316 0.02701561]
 [8.         7.5534414  4.25308709 1.73277247 0.72069014 0.29932181
  0.12428631 0.05403123]]

Указание точек, в которых требуется решение.

>>> sol = solve_ivp(exponential_decay, [0, 10], [2, 4, 8],
...                 t_eval=[0, 1, 2, 4, 10])
>>> print(sol.t)
[ 0  1  2  4 10]
>>> print(sol.y)
[[2.         1.21305369 0.73534021 0.27066736 0.01350938]
 [4.         2.42610739 1.47068043 0.54133472 0.02701876]
 [8.         4.85221478 2.94136085 1.08266944 0.05403753]]

Снаряд, выпущенный вверх с терминальным событием при ударе. terminal и direction поля события применяются путём модификации функции на лету. Здесь y[0] является позицией и y[1] является скоростью. Снаряд начинает движение в позиции 0 со скоростью +10. Обратите внимание, что интегрирование никогда не достигает момента t=100, так как событие является терминальным.

>>> def upward_cannon(t, y): return [y[1], -0.5]
>>> def hit_ground(t, y): return y[0]
>>> hit_ground.terminal = True
>>> hit_ground.direction = -1
>>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10], events=hit_ground)
>>> print(sol.t_events)
[array([40.])]
>>> print(sol.t)
[0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02
 1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]

Используйте dense_output и события чтобы найти позицию, которая равна 100, в вершине траектории пушечного ядра. Вершина не определена как конечная точка, поэтому найдены и вершина, и точка удара о землю. Нет информации при t=20, поэтому используется атрибут sol для вычисления решения. Атрибут sol возвращается при установке dense_output=True. Альтернативно, y_events атрибут можно использовать для доступа к решению в момент события.

>>> def apex(t, y): return y[1]
>>> sol = solve_ivp(upward_cannon, [0, 100], [0, 10],
...                 events=(hit_ground, apex), dense_output=True)
>>> print(sol.t_events)
[array([40.]), array([20.])]
>>> print(sol.t)
[0.00000000e+00 9.99900010e-05 1.09989001e-03 1.10988901e-02
 1.11088891e-01 1.11098890e+00 1.11099890e+01 4.00000000e+01]
>>> print(sol.sol(sol.t_events[1][0]))
[100.   0.]
>>> print(sol.y_events)
[array([[-5.68434189e-14, -1.00000000e+01]]),
 array([[1.00000000e+02, 1.77635684e-15]])]

В качестве примера системы с дополнительными параметрами мы реализуем уравнения Лотки-Вольтерры [12].

>>> def lotkavolterra(t, z, a, b, c, d):
...     x, y = z
...     return [a*x - b*x*y, -c*y + d*x*y]
...

Мы передаем значения параметров a=1.5, b=1, c=3 и d=1 с помощью args аргумент.

>>> sol = solve_ivp(lotkavolterra, [0, 15], [10, 5], args=(1.5, 1, 3, 1),
...                 dense_output=True)

Вычислить плотное решение и построить его график.

>>> t = np.linspace(0, 15, 300)
>>> z = sol.sol(t)
>>> import matplotlib.pyplot as plt
>>> plt.plot(t, z.T)
>>> plt.xlabel('t')
>>> plt.legend(['x', 'y'], shadow=True)
>>> plt.title('Lotka-Volterra System')
>>> plt.show()

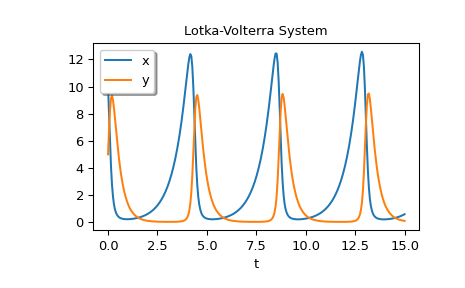
Несколько примеров использования solve_ivp для решения дифференциального уравнения y' = Ay со сложной матрицей A.

>>> A = np.array([[-0.25 + 0.14j, 0, 0.33 + 0.44j],
...               [0.25 + 0.58j, -0.2 + 0.14j, 0],
...               [0, 0.2 + 0.4j, -0.1 + 0.97j]])

Решение задачи Коши с A сверху и y как вектор 3x1:

>>> def deriv_vec(t, y):
...     return A @ y
>>> result = solve_ivp(deriv_vec, [0, 25],
...                    np.array([10 + 0j, 20 + 0j, 30 + 0j]),
...                    t_eval=np.linspace(0, 25, 101))
>>> print(result.y[:, 0])
[10.+0.j 20.+0.j 30.+0.j]
>>> print(result.y[:, -1])
[18.46291039+45.25653651j 10.01569306+36.23293216j
 -4.98662741+80.07360388j]

Решение задачи Коши с A сверху с y как матрица 3x3 :

>>> def deriv_mat(t, y):
...     return (A @ y.reshape(3, 3)).flatten()
>>> y0 = np.array([[2 + 0j, 3 + 0j, 4 + 0j],
...                [5 + 0j, 6 + 0j, 7 + 0j],
...                [9 + 0j, 34 + 0j, 78 + 0j]])

>>> result = solve_ivp(deriv_mat, [0, 25], y0.flatten(),
...                    t_eval=np.linspace(0, 25, 101))
>>> print(result.y[:, 0].reshape(3, 3))
[[ 2.+0.j  3.+0.j  4.+0.j]
 [ 5.+0.j  6.+0.j  7.+0.j]
 [ 9.+0.j 34.+0.j 78.+0.j]]
>>> print(result.y[:, -1].reshape(3, 3))
[[  5.67451179 +12.07938445j  17.2888073  +31.03278837j
    37.83405768 +63.25138759j]
 [  3.39949503 +11.82123994j  21.32530996 +44.88668871j
    53.17531184+103.80400411j]
 [ -2.26105874 +22.19277664j -15.1255713  +70.19616341j
   -38.34616845+153.29039931j]]

НазадОткрыть во вкладке