scipy.interpolate.

Akima1DInterpolator#

класс scipy.interpolate.Akima1DInterpolator(x, y, ось=0, *, метод='akima', экстраполяция=None)[источник]#

Интерполятор Акимы "визуально приятный" (гладкость C1).

Аппроксимировать кусочно-кубические полиномы, заданные векторами x и y. Метод интерполяции Акимы использует непрерывно дифференцируемый суб-сплайн, построенный из кусочно-кубических полиномов. Полученная кривая проходит через заданные точки данных и будет выглядеть гладкой и естественной.

Параметры:

xndarray, форма (npoints, ): 1-D массив монотонно возрастающих вещественных значений.
yndarray, форма (..., npoints, ...): N-мерный массив действительных значений. Длина y вдоль оси интерполяции должен быть равен длине x. Используйте axis параметр для выбора оси интерполяции.
осьint, необязательный: Ось в y массив, соответствующий значениям x-координаты. По умолчанию равен axis=0.
метод{‘akima’, ‘makima’}, опционально: Если "makima", используйте модифицированную интерполяцию Акимы [2]. По умолчанию "akima", используйте интерполяцию Акимы [1].

Добавлено в версии 1.13.0.
экстраполяция{bool, None}, опционально: Если bool, определяет, следует ли экстраполировать на точки вне границ на основе первого и последнего интервалов или возвращать NaN. Если None, extrapolate установлено в False.

Атрибуты:

ось
c
экстраполяция
x

Методы

`__call__`(x[, nu, extrapolate])	Вычислить кусочно-полиномиальную функцию или её производную.
`derivative`([nu])	Создать новый кусочно-полиномиальный объект, представляющий производную.
`antiderivative`([nu])	Создать новый кусочно-полиномиальный объект, представляющий первообразную.
`integrate`(a, b[, extrapolate])	Вычислить определённый интеграл по кусочно-полиномиальной функции.
`solve`([y, разрыв, экстраполяция])	Найти вещественные решения уравнения `pp(x) == y`.
`roots`([discontinuity, extrapolate])	Найти вещественные корни кусочно-полиномиальной функции.

Смотрите также

PchipInterpolator: PCHIP 1-D монотонный кубический интерполятор.
CubicSpline: Кубический сплайн-интерполятор данных.
PPoly: Кусочно-полиномиальная функция в терминах коэффициентов и точек разрыва

Примечания

Добавлено в версии 0.14.

Используйте только для точных данных, так как подобранная кривая проходит через заданные точки точно. Эта процедура полезна для построения приятно гладкой кривой через несколько заданных точек для целей визуализации.

Пусть \(\delta_i = (y_{i+1} - y_i) / (x_{i+1} - x_i)\) будут наклонами интервала \(\left[x_i, x_{i+1}\right)\). Производная Акимы в \(x_i\) определяется как:

\[d_i = \frac{w_1}{w_1 + w_2}\delta_{i-1} + \frac{w_2}{w_1 + w_2}\delta_i\]

В интерполяции Акимы [1] (method="akima"), веса:

\[\begin{split}\begin{aligned} w_1 &= |\delta_{i+1} - \delta_i| \\ w_2 &= |\delta_{i-1} - \delta_{i-2}| \end{aligned}\end{split}\]

В модифицированной интерполяции Акимы [2] (method="makima"), чтобы устранить перерегулирование и избежать граничных случаев, когда и числитель, и знаменатель равны 0, веса модифицируются следующим образом:

\[\begin{split}\begin{align*} w_1 &= |\delta_{i+1} - \delta_i| + |\delta_{i+1} + \delta_i| / 2 \\ w_2 &= |\delta_{i-1} - \delta_{i-2}| + |\delta_{i-1} + \delta_{i-2}| / 2 \end{align*}\end{split}\]

Ссылки

[1] (1,2)

Новый метод интерполяции и сглаживания кривых, основанный на локальных процедурах. Хироши Акима, J. ACM, октябрь 1970, 17(4), 589-602. DOI:10.1145/321607.321609

[2] (1,2)

Интерполяция кубическими полиномами Макимы. Клив Молер и Космин Ионица, 2019. https://blogs.mathworks.com/cleve/2019/04/29/makima-piecewise-cubic-interpolation/

Примеры

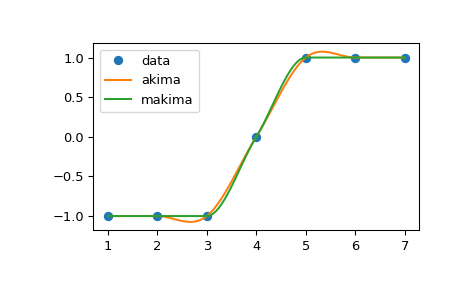
Сравнение method="akima" и method="makima":

>>> import numpy as np
>>> from scipy.interpolate import Akima1DInterpolator
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(1, 7, 7)
>>> y = np.array([-1, -1, -1, 0, 1, 1, 1])
>>> xs = np.linspace(min(x), max(x), num=100)
>>> y_akima = Akima1DInterpolator(x, y, method="akima")(xs)
>>> y_makima = Akima1DInterpolator(x, y, method="makima")(xs)

>>> fig, ax = plt.subplots()
>>> ax.plot(x, y, "o", label="data")
>>> ax.plot(xs, y_akima, label="akima")
>>> ax.plot(xs, y_makima, label="makima")
>>> ax.legend()
>>> fig.show()

Превышение, произошедшее в "akima" было избегнуто в "makima".

../../_images/scipy-interpolate-Akima1DInterpolator-1.png